


БНБ
"БРОКГАУЗ И ЕФРОН" (121188)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Числительные имена
Определение "Числительные имена" в словаре Брокгауза и Ефрона
Числительные имена (грамм.). — Понятие численности в языке выражается двумя способами: 1) в виде особых форм имени, местоимения и глагола, обозначающих общие представления так называемого единственного, двойственного и множественного "чисел" (см.), и 2) в виде самостоятельных имен Ч., означающих точные понятия отдельных чисел. Оба способа до известной степени связаны друг с другом исторически, причем иногда связь эта дает себя знать долго спустя после того, как известные формальные особенности уже потеряли всякое реальное значение. Так, до сих пор в русском языке Ч. два соединяется с древними формами двойственного числа имен существительных (только в муж. роде), хотя двойственное число само давно уже перестало существовать (например, два брата). В свою очередь и самостоятельные формы двойственного числа нередко удерживаются лишь у имен Ч., хотя другими именами давно уже утрачены (ср., например, русское и вообще славянское два, рус. двумя, двух, лат. octô и т. д.). Развитие имен Ч. в языках находится в заметной связи с языком жестов. Нередко можно наблюдать, что жест, как более простое и более понятное средство выражения, даже задерживает развитие самостоятельного языкового обозначения чисел. Недостаточное развитие имен Ч. как раз наблюдается в языках тех племен, которые до сих пор обладают богатым языком жестов, параллельным со звуковой речью или нередко заменяющим ее. Поэтому надо остерегаться делать слишком поспешные заключения о невыработанности числовых понятий или вообще о неспособности к счету таких народов, на основании недостаточности их числительных систем. Так, едва ли существует какая-нибудь существенная разница между числовыми представлениями индейцев чиквито и тарахумара (в Мексике), хотя первые имеют особое слово только для понятия 1 и все остальные числа выражают поднятием пальцев, а вторые, рядом с жестами пальцев, произносят особые определенные звуки. Первичная связь имен Ч. с языком жестов, а именно пальцев руки, отражается в громадном распространении десятичной системы счисления на всем земном шаре, при отсутствии которой мы чаще всего встречаемся с системами пятеричной и "двадцатеричной" (вигезимальной), восходящими к тому же естественному способу счета по пальцам, с той разницей, что в основе пятеричной системы лежит только одна рука, а при двадцатеричной привлекаются к счету еще и ножные пальцы. Индейцы Америки до сих пор в своем языке жестов обозначают число 20, вытягивая все 10 пальцев по направлению к ногам, а эскимосы то же число выражают сочетанием слов "кончен весь человек", т. е. "кончен" счет всех его пальцев на руках и на ногах. Рядом с названными системами, у некоторых южно-американских и у большинства австралийских племен встречаются следы известной связи имен Ч. с личными местоимениями. По-видимому, первый толчок к образованию Ч. имен был здесь дан именно отличением собственной особы от другого лица, к которому обращаются с речью, и от третьего лица — отличением, легшим в основу образования форм единственного числа личных местоимений. Впрочем, и здесь, рядом с этим первичным способом счета, встречаются осколки пятеричной и двадцатеричной систем. Так, в абипонском языке самостоятельные слова Ч. имеются только для 1 и 2, понятие же 3 выражается соединением 2+1, но рядом имеются еще выражения: "пальцы страусовой ноги" (4), "пальцы руки" (5), "пальцы обеих рук" (10), "пальцы обеих рук и обеих ног" (20). Исключение составляет язык тасманцев (теперь уже вымерший), в котором самостоятельные Ч. имеются для первых четырех чисел, а 5 выражается, как 4+1. Возможно, впрочем, что и здесь число 4 первично выражалось именем какого-нибудь предмета, состоявшего из четырех частей (как в абипонском). На таком первичном счете, вероятно, основано особое значение числа3, свойственное семитам и индоевропейцам, отразившееся в "шестеричном" счете по шестеркам, дюжинам, "гроссам" и т. д., следы которого несомненно существуют и в индоевропейских языках, и дали повод И. Шмидту сделать неправдоподобное предположение, что прародина индоевропейцев находилась в Азии, вблизи Вавилона, где также существовал шестеричный счет и откуда индоевропейцы только и могли его заимствовать. Из вышеизложенного, однако, ясно, что шестеричный счет не составляет монополии семитов и в глубокой древности мог возникнуть у индоевропейцев самостоятельно. Главную роль в образовании Ч. играют, однако, конкретные названия руки и пальцев, которые со временем превращаются в имена абстрактных числовых понятий. Следы этого процесса найдем и в индоевропейской системе Ч., где, например, первичное Ч. *penge = санскрит. раńса, лит. penki, греч. πέντε, лат. quinque (из *pinque) = 5, находится в этимологическом родстве с древневерхненемецким fûst = нем. Faust, старослав. 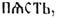 , польск. pięść, đус. пясть, пясточка (горсть), запястье, и первично, очевидно, имело значение просто "рука". Нет ничего невероятного, что другие имена Ч., подобно абипонскому "нога страуса" = 4, тоже восходят к различным конкретным именам, хотя все существующие попытки доказать это положение являются чистыми догадками. Применяясь к другим предметам, состоящим из стольких же одинаковых частей, или к собраниям стольких же одинаковых предметов, подобные конкретные названия мало-помалу утрачивали свое конкретное предметное значение и переходили в простые Ч. Таким образом, нет ничего удивительного в общем распространении десятичной системы Ч., рядом с которой являются менее совершенные пятеричная и двадцатеричная системы, служащие большей частью дополнениями десятичной (вроде франц. q u atrevingt = 80, рядом с десятичными Ч.). Лишь немногие народы (например, негры Динка) имеют настоящие пятеричные системы, в которых основой счета является 5, и Ч., следующие за ним, образуются путем сложения: 5+1, 5+2 и т. д. В индоевропейской системе Ч. основным числом является 10, и Ч., следующие за ним, образуются путем сложения, вроде русского 11 = один-на-дцать (1+10), 12 = две-на-дцать (2+10) и т. д. Ч. 20, как в славянском (два-десять, рус. два-дцать), так и в других индоевропейских языках, тоже восходит к сложению из Ч. два и сокращенного десять (санскрит. vi-çati, лат. vi-ginti, греч. дорич. Fι - κατι, F εί - κατι, аттич. εΐ - κοσι). Даже 100 = индоевропейскому *k'mto-m представляет собой первичное *dk'm-to-m, т. е. "десяток" (подразумевается, "десятков"). Таким образом основными Ч. в индоевропейских языках являются только первые 10. Остальные уже в индоевропейском праязыке являлись составными из этих 10, причем частью это были сложные слова. О том, что по крайней мере известная часть диалектов индоевропейского праязыка имела уже понятие о 1000, свидетельствуют Ч. санскрит. sa-hàsram (=одна тысяча), греч. лесб. χέλλιοι из χεσλιοι (аттич. χίλιοι), в основе которых лежит индоевропейское *g'heslo. Рядом с этим образованием темного происхождения, имелись, вероятно, и вполне ясные сложения, вроде санскрит. daç açatî, т. е. 10 сотен = 1000. Славянское
, польск. pięść, đус. пясть, пясточка (горсть), запястье, и первично, очевидно, имело значение просто "рука". Нет ничего невероятного, что другие имена Ч., подобно абипонскому "нога страуса" = 4, тоже восходят к различным конкретным именам, хотя все существующие попытки доказать это положение являются чистыми догадками. Применяясь к другим предметам, состоящим из стольких же одинаковых частей, или к собраниям стольких же одинаковых предметов, подобные конкретные названия мало-помалу утрачивали свое конкретное предметное значение и переходили в простые Ч. Таким образом, нет ничего удивительного в общем распространении десятичной системы Ч., рядом с которой являются менее совершенные пятеричная и двадцатеричная системы, служащие большей частью дополнениями десятичной (вроде франц. q u atrevingt = 80, рядом с десятичными Ч.). Лишь немногие народы (например, негры Динка) имеют настоящие пятеричные системы, в которых основой счета является 5, и Ч., следующие за ним, образуются путем сложения: 5+1, 5+2 и т. д. В индоевропейской системе Ч. основным числом является 10, и Ч., следующие за ним, образуются путем сложения, вроде русского 11 = один-на-дцать (1+10), 12 = две-на-дцать (2+10) и т. д. Ч. 20, как в славянском (два-десять, рус. два-дцать), так и в других индоевропейских языках, тоже восходит к сложению из Ч. два и сокращенного десять (санскрит. vi-çati, лат. vi-ginti, греч. дорич. Fι - κατι, F εί - κατι, аттич. εΐ - κοσι). Даже 100 = индоевропейскому *k'mto-m представляет собой первичное *dk'm-to-m, т. е. "десяток" (подразумевается, "десятков"). Таким образом основными Ч. в индоевропейских языках являются только первые 10. Остальные уже в индоевропейском праязыке являлись составными из этих 10, причем частью это были сложные слова. О том, что по крайней мере известная часть диалектов индоевропейского праязыка имела уже понятие о 1000, свидетельствуют Ч. санскрит. sa-hàsram (=одна тысяча), греч. лесб. χέλλιοι из χεσλιοι (аттич. χίλιοι), в основе которых лежит индоевропейское *g'heslo. Рядом с этим образованием темного происхождения, имелись, вероятно, и вполне ясные сложения, вроде санскрит. daç açatî, т. е. 10 сотен = 1000. Славянское 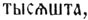 , готск. thûsundi, древневерхненем. dûsunt, нем. Thausend, лит. túkstantis представляют собой другую древнюю форму, также свойственную еще известной части диалектов индоевропейского праязыка. У индоевропейских Ч. принято различать следующие классы: Ч. количественные (cardinalia), отвлеченные (abstracta), порядковые (ordinalia), множительные (multiplicativa) и распределительные (distributiva). Нередко наблюдается переход Ч. из одного класса в другой. Так, славянское
, готск. thûsundi, древневерхненем. dûsunt, нем. Thausend, лит. túkstantis представляют собой другую древнюю форму, также свойственную еще известной части диалектов индоевропейского праязыка. У индоевропейских Ч. принято различать следующие классы: Ч. количественные (cardinalia), отвлеченные (abstracta), порядковые (ordinalia), множительные (multiplicativa) и распределительные (distributiva). Нередко наблюдается переход Ч. из одного класса в другой. Так, славянское  , русское пять, представляет собой в сущности не количественное, а отвлеченное имя существительное Ч. (пяток, пятерка), родственное санскритскому аналогичному имени pankti-s и подчинившееся, кроме того, влиянию порядкового числительного
, русское пять, представляет собой в сущности не количественное, а отвлеченное имя существительное Ч. (пяток, пятерка), родственное санскритскому аналогичному имени pankti-s и подчинившееся, кроме того, влиянию порядкового числительного 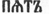 (ср. греч. πέμπτος), по типу отношений десять — десятый, девять — девятый и т. д. Вместо индоевропейского настоящего количественного *penqe, в старославянском было бы
(ср. греч. πέμπτος), по типу отношений десять — десятый, девять — девятый и т. д. Вместо индоевропейского настоящего количественного *penqe, в старославянском было бы 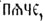 а в русском *пяче. Точно так же и вместо санскрит. pankti-s должно было бы получиться старославянское
а в русском *пяче. Точно так же и вместо санскрит. pankti-s должно было бы получиться старославянское 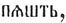 русское *пячь (ср. лат. nох, nocti-s, старослав. ношть, рус. ночь). Таким образом форма пять не могла возникнуть фонетически ни из индоевропейского *penqe, ни из индоевропейского *penqti-s и может быть объяснена лишь аналогией или морфологической ассимиляцией к порядковому пятый. Такие же случаи представляют и следующие славянские Ч. количественные: шесть (от шестой), седмь, семь (от седьмой, ср. греч. έβδομος, лат. septimus, лит. septimas), восемь, осмь (от осмой). Некоторые Ч., согласно с вышеизложенным, обнаруживают родство с местоимениями. Так, например, одна из индоевропейских форм Ч. количественно 1 образована от несомненно местоименного корня оi-; ср. греко-итало-кельто-германо-балтийско-славянское *oi-no-s (греч. οί - νό - ς "одно очко на игральной кости", лат. unus "один", готск. àin-s, нем. ein, лит. v-ënas, слав. инъ, например в ино-рог = единорог; сюда же санскрит. êna— в значении местоимения "он", первично, вероятно, просто указательного), инд. oi-qo = санскрит. ê-ka-s "один" и т. д. Другие Ч., напротив, могут быть приведены в связь с глагольными корнями. Таково, например, порядковое Ч. для 1: старослав. прьвъ, рус. первый, санскрит. pûrvas "находящийся впереди", греч. πρώτος и т. д., лат. prîmus, лит. pìrmas и др., находящиеся в родстве с глагольным корнем реr-роr-, имеющимся в нашем переть, пороть, паром (собственно, пором), греч. περάω "переправляюсь, двигаюсь вперед" и т. д. Таково же наше Ч. новейшего происхождения раз, тождественное со второй частью слова образ, корнем глагола раз-ить и именем существительным раз, рядом с которыми имеем глагол резать, сохранивший до сих пор основное значение корня. Первичное значение раз было — черта, проведенная острым орудием, нарезка. Во второй части Ч. прилагательных двукратный, трехкратный, наречиях двукраты, трикраты, польск. dwukroć и т. д. имеем также элемент глагольного происхождения, являющийся семасиологической параллелью к раз— (крата = первично черта, от корня qert-, qort— "резать, рубить"). Таким образом, Ч. не представляют исключения среди других грамматических категорий по какой-либо особенной чистоте и однородности своего состава и являются таким же конгломератом первично разнородных частей, как, например, предлоги, суффиксы, имена и т. п.
русское *пячь (ср. лат. nох, nocti-s, старослав. ношть, рус. ночь). Таким образом форма пять не могла возникнуть фонетически ни из индоевропейского *penqe, ни из индоевропейского *penqti-s и может быть объяснена лишь аналогией или морфологической ассимиляцией к порядковому пятый. Такие же случаи представляют и следующие славянские Ч. количественные: шесть (от шестой), седмь, семь (от седьмой, ср. греч. έβδομος, лат. septimus, лит. septimas), восемь, осмь (от осмой). Некоторые Ч., согласно с вышеизложенным, обнаруживают родство с местоимениями. Так, например, одна из индоевропейских форм Ч. количественно 1 образована от несомненно местоименного корня оi-; ср. греко-итало-кельто-германо-балтийско-славянское *oi-no-s (греч. οί - νό - ς "одно очко на игральной кости", лат. unus "один", готск. àin-s, нем. ein, лит. v-ënas, слав. инъ, например в ино-рог = единорог; сюда же санскрит. êna— в значении местоимения "он", первично, вероятно, просто указательного), инд. oi-qo = санскрит. ê-ka-s "один" и т. д. Другие Ч., напротив, могут быть приведены в связь с глагольными корнями. Таково, например, порядковое Ч. для 1: старослав. прьвъ, рус. первый, санскрит. pûrvas "находящийся впереди", греч. πρώτος и т. д., лат. prîmus, лит. pìrmas и др., находящиеся в родстве с глагольным корнем реr-роr-, имеющимся в нашем переть, пороть, паром (собственно, пором), греч. περάω "переправляюсь, двигаюсь вперед" и т. д. Таково же наше Ч. новейшего происхождения раз, тождественное со второй частью слова образ, корнем глагола раз-ить и именем существительным раз, рядом с которыми имеем глагол резать, сохранивший до сих пор основное значение корня. Первичное значение раз было — черта, проведенная острым орудием, нарезка. Во второй части Ч. прилагательных двукратный, трехкратный, наречиях двукраты, трикраты, польск. dwukroć и т. д. имеем также элемент глагольного происхождения, являющийся семасиологической параллелью к раз— (крата = первично черта, от корня qert-, qort— "резать, рубить"). Таким образом, Ч. не представляют исключения среди других грамматических категорий по какой-либо особенной чистоте и однородности своего состава и являются таким же конгломератом первично разнородных частей, как, например, предлоги, суффиксы, имена и т. п.
Литература. Бопп, "Ueber die Zahlwörter im Sanskr., Griech., Lat., Litth., Goth. und Altslaw" ("Abhandlungen" берлинской академии, 1833); Лепсиус, "Ueber den Ursprung und die Verwandtschaft der Zahlwörter in der Indogerm., Semit. und der Koptischen Sprache", в его "Zwei sprachvergleichende Abhandlungen" (Б., 1836); Потт, "Die quinä re und vigesimale Zählmethode bei Völkern aller Welttheile, nebst ausführlichen Bemerkungen über die Zahlwörter Indogermanischen Stammes" (Г алле, 1847); его же, "Die Sprachverschiedenheit in Europa an den Zahlwö rtern nachgewiesen, sowie die quinäre und vigesimale Zählmethode" (т ам же, 1868); Э. Шрадер, "Ueber den Ursprung und die Bedeutung der Zählwörter in der indoeurop. Sprache" (С тендаль, 1854); Zehetmayr, "Verbalbedeutung der Zahlwö rter, als Beitrag zur Beleuchtung des ursprüngl. Verhältnisses der indogerm. Sprachen zum semit. Sprachstamme" (Л ейпциг, 1854); В. Вакернагель, "Ueber Zahl und Ziffern" (Michaelis, "Zeitschr. fü r Stenographie", 1855); Benloew, "Recherches sur l'origine des noms de nombre japhétiques et sémitiques" (Г иссен, 1861); Краузе, "Ueb. den Ursprung und die Bedeutung der Zahlwö rter" ("Zeitschr. f. öster reich. Gymnasien", 1865); И. Шмидт, "Ueber einige numeralia multiplicativa" (Кун, "Zeitschr. f. vergl. Sprachforschung"); Эд. Мюллер, "Sprachvergleichendes üb. die Numeralia" (Флекейзен, "Jahrbücher f. class. Philologie", т. 97); Асколи, "Ueb. eine Gruppe indogermanischer Endungen" ("Kritische Studien"); Шерер, "Zur Geschichte der deutschen Sprache" (2-е изд., стр. 576 и сл.); Остгофф, "Formassociation bei Zahlwörtern" ("Morphologische Untersuchungen", I); Баупак, "Formassociation bei den indogerm. Numeralien etc." (Кун, "Zeitschr. f. vergl. Sprachforschung"); Бругман, "Die Bildung der Zehner und der Hunderter in den idg. Sprachen" ("Morphologische Untersuchungen"); Вундт, "Völkerpsychologie" (т. I, ч. 2, Лейпциг, 1900, стр. 24-31); Фриц Шульце, "Psychologie der Naturvölker" (1900, стр. 56). Сравнительно-грамматическое освещение: Бопп, "Vergleich. Grammatik der indogerm. Sprachen" (т. II, 3); А. Шлейхер, "Compendium der vergleich. Grammatik" (4 изд.); Бругман, "Grundriss der vergleich. Grammatik der indogerm. Sprachen" (т. II, ч. 2, стр. 463-510, Страсбург, 1892), где указана и прочая литература по отдельным индоевропейским языкам.
С. Б-ч.
| "БРОКГАУЗ И ЕФРОН" >> "Ч" >> "ЧИ" >> "ЧИС" |
Статья про "Числительные имена" в словаре Брокгауза и Ефрона была прочитана 1132 раз
| Гороховое пюре |
| Панайпай |
TOP 15
- Волос
- Проно
- Степные животные
- Гимнастика
- Индийский океан
- Архитектура
- Сравнение, в литературе
- Манда
- Клитры
- Колесование
- Испарение
- Травоядные животные
- Оплодотворение у pacтений
- Вредные насекомые
- Электризация тел