


БНБ
"БРОКГАУЗ И ЕФРОН" (121188)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Циссоида
Определение "Циссоида" в словаре Брокгауза и Ефрона
Циссоида — была изобретена Диоклом (см.). Она получается при помощи следующего построения. Представим себе круг, касающейся прямой DBE в точке В. Через точку А, конец диаметра АВ, проведем луч АС до пересечения с прямой DBE в точке С.
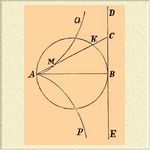
Обозначим буквою К точку пересечения этого луча с окружностью данного круга. Если на АС отложим отрезок АМ = КС, то получим точку X, принадлежащую Ц.
Уравнение этой кривой, отнесенной к прямоугольной системе координат, имеет вид
y2 = x3/(2a — x).
Здесь a — радиус круга АКВ; начало координат взято в точке Α и ось x- ов совпадает с прямою AB.
Точка А есть точка возврата кривой, а de — ее прямолинейная асимптота.
Площадь, ограниченная кривою PAQ и ее асимптотой DE, равна 3 π a2.
Д. С.
| "БРОКГАУЗ И ЕФРОН" >> "Ц" >> "ЦИ" >> "ЦИС" |
Статья про "Циссоида" в словаре Брокгауза и Ефрона была прочитана 1338 раз
| Коптим скумбрию в коробке |
| Английская картошка фри |
TOP 15
- Волос
- Проно
- Степные животные
- Гимнастика
- Индийский океан
- Архитектура
- Сравнение, в литературе
- Манда
- Клитры
- Колесование
- Испарение
- Травоядные животные
- Оплодотворение у pacтений
- Вредные насекомые
- Электризация тел