Хладниевы фигуры

Значение слова "Хладниевы фигуры" в Энциклопедическом словаре Брокгауза и Ефрона

Хладниевы фигуры(см. Хладни) — Образуются такие фигуры на горизонтальных тонких пластинках (стеклянных, металлических и др.), зажатых или прикрепленных посередине (или в другом месте) и посыпанных мелким сухим песком, когда смычком приводят их в поперечные колебания. При этом песок сбрасывается с тех мест, которые находятся в более сильном колебании (так называемый пучности), и располагается в местах, где колебаний нет или они незначительны (именно, по узловым линиям). Полученные таким образом фигуры могут быть очень разнообразны.

Фиг. 3. Способ воспроизведения фигур.

Вид их зависит как от формы пластинки, так и от места ее закрепления, а также и от тех мест, в которых проводят смычком и прикасаются пальцем (для задержания колебания и образования узла).

Фиг. 4. Способ закрепления пластинок.

Кроме того, влияние оказывает и степень нажатия смычка и скорость его движения. На квадратных пластинках наиболее простые фигуры получаются в виде креста, расположенного или параллельно сторонам или по диагоналям (фиг. 1).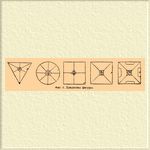

Фиг. 1. Хладниевы фигуры.

Можно получить и более сложные фигуры (фиг. 2).

Фиг. 2. Сложные фигуры на квадратных пластинках.

На круглых пластинках получаются вообще звездообразные фигуры. Каждой фигуре соответствует определенный тон; притом, чем сложнее фигура, тем тон выше. Для прямоугольных пластинок объяснение сводится к образованию двух систем взаимно-перпендикулярных стоячих волн (Витстон — Wheatstone). Теория колебаний пластинок наиболее полно разработана Кирхгофом (Kirchhoff, "Gesammelte Abhandlungen"). Хладни нашел, что при одинаковых материале и форме пластинок и при одном и том же способе возбуждения колебаний в них, частота колебаний т. е. число колебаний в секунду, N, пропорциональна толщине е и обратно пропорциональна поверхности s; след., N = K·(e)/(s). Теория же дает K = k√E/D (где Е модуль упругости, D плотность и k численный коэффициент).

Более обстоятельные сведения по данному вопросу можно почерпнуть, между прочим, в "Курсе физики" О. Д. Хвольсона (II, 57); в "Акустике" Н. П. Слугинова и в других подробных руководствах.

Н. Г.

В Энциклопедическом словаре Брокгауза и Ефрона рядом со словом "Хладниевы фигуры"

Хладни, Эрнст Флоренс Фридрих | Буква "Х" | В начало | Буквосочетание "ХЛ" | Хладноломкость

Статья про слово "Хладниевы фигуры" в Энциклопедическом словаре Брокгауза и Ефрона была прочитана 5 раз

Брокгауз и Ефрон, избраное

Булль-Рон
Голубинский, Дмитрий Федорович
Тегнер Ганс
Шефер, Дитрих

Seafood restaurants in USA - short guide