


БНБ
"БРОКГАУЗ И ЕФРОН" (121188)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Химические равновесия
Определение "Химические равновесия" в словаре Брокгауза и Ефрона
Химические равновесия — Явления химического равновесия охватывают область неполных превращений, т. е. таких случаев, когда химическое превращение материальной системы совершается не до конца, но прекращается после того, как изменению подвергнется часть вещества. В подобных случаях конечным результатом химической реакции является не исчезновение взятых тел и образование новых (одного или нескольких), ранее в системе не заключавшихся, а достижение такого состояния системы, при котором одновременно и совместно существуют и исходные, и образовавшиеся при реакции тела, не испытывая уже дальнейшего превращения. При определенных условиях, такое состояние устанавливается тогда, когда между количествами исходных и полученных тел будет достигнуто определенное отношение, когда будет, как говорят, достигнут предел, и раз этот предел будет достигнут, система способна существовать, не изменяясь, бесконечное время, хотя и будет заключать в себе тела, способные при другом количественном отношении испытывать превращение. Таким образом, в таких системах тела, способные испытывать превращения, остаются без изменения в состоянии равновесия. Общей причиной существования такого равновесия является то обстоятельство, что при одних и тех условиях температуры и давления, химическое превращение может совершаться в двух противоположных направлениях, другими словами, оно обратимо. Система А превращается в систему В, но при этих же условиях и система В превращается в систему А. Очевидно, что ни одно и ни другое превращение не могут совершиться сполна, но должна получиться система, заключающая и А, и B, должно установиться некоторое среднее положение, при котором тела А и В будут находиться в равновесии. Характерным свойством такого химического равновесия будет то, что оно является равновесием устойчивым, так как всякое отклонение от состояния равновесия непременно вызовет в системе реакцию, которая приведет систему к прежнему состоянию равновесия. Оно также будет подвижным равновесием, так как изменение условий равновесия вызовет в системе такие превращения, которые приведут систему к новому состоянию равновесия, тоже устойчивого. Общие законы и характер химических равновесий изложены в статьях Правило фаз и Обратимость химических реакций (см.), здесь же мы познакомимся с количественной стороной вопроса и с приложением термодинамики для решения вопроса о том, как изменяется химическое превращение под влиянием различных условий. При всех химических превращениях состояние равновесия обуславливается тремя величинами: количествами действующих тел, или их массами, температурой и давлением. Самый характер равновесия может быть, в зависимости от числа действующих тел и от числа фаз, троякого рода: или возможно только одно состояние равновесия при совершенно определенных температуре и давлении, или равновесие возможно при различных температурах, причем при каждой температуре возможно только одно состояние равновесия, или, наконец, при каждой температуре существует бесчисленное множество состояний равновесия. Какое из этих трех равновесий приложимо в каждом данном случае — это определяется правилом фаз. Наша задача заключается в том, чтобы определить, как будет изменяться состояние равновесия, т. е. предел реакции, в зависимости от изменения трех переменных: массы действующих тел, температуры и давления.
1) Влияние массы. Ясное и точное представление о влиянии массы на X. равновесие впервые было введено Гульдбергом и Вааге в их знаменитом мемуаре: "Исследование сил X. сродства". В этом сочинении они высказали закон масс, по которому X. действие пропорционально произведению действующих масс. Их идеи вполне подтвердились последующими исследованиями, и в настоящее время их теория является общепринятой, отличаясь только терминологией, так как Гульдберг и Вааге пользовались термином сила сродства, который в настоящее время оставлен. Чтобы показать, в чем заключается их теория, приводим их подлинные слова, заметив только, что под термином действующая масса они подразумевали "количества тела, которые находятся в 1 куб. см целого объема".
"Предположим, что через двойное замещение два тела А и В превращаются в два новые тела A' и В' и что при тех же условиях A' и В' могут превратиться в А и В. Тогда ни образование А' и В', ни обратное образование А и B не будут полными; в конце реакции всегда будем иметь четыре тела A, В, Α ' Β ', и сила, вызывающая образование А' и В', будет уравновешена силою, вызывающей образование А и В".
"Сила, вызывающая образование А' и В' возрастает пропорционально коэффициенту сродства для реакции
А + В = А' + В',
но сверх того она зависит от массы А и B. Мы вывели из наших опытов, что сила пропорциональна произведению действующих масс тел А и В. Обозначим действующие массы тел А и В через p и q и коэффициент сродства через k, — получим, что сила = kpq". "Как мы несколько раз указывали, сила kpq, или сила между А и B, не есть единственная, которая действует во время реакции. Существуют другие силы, которые стремятся ускорить или замедлить образование А' и В'. Однако, предположим, что других сил нет, и посмотрим, как выразятся в этом случае формулы".
"Мы думаем, что изучение этой идеальной реакции, при которой рассматриваются только силы между А и В и между А' и В', даст читателям ясную и точную идею нашей теории".
"Пусть действующие массы тел А' и В' равны p' и q', и коэффициент сродства для реакции
А' + В' = А + В
равен k'; тогда сила, которая производит обратное образование А и В равна k'p'q'. Эта сила уравновешена первой силой, и, следовательно, имеем:
kpq = k'p'q'
Определяя действующие массы p, q, p' и q' из опытов, можно найти отношение между коэффициентами сродства k и k'. С другой стороны, найдя это отношение, можно наперед вычислить результат реакции для любого начального состояния четырех тел". Приведенная выдержка показывает, как определяется на основании закона действия массы состояние равновесия для частного случая — превращения
А + В = А' + В'.
В настоящее время уравнение равновесия может быть выведено для общего случая, когда в реакции участвует несколько тел в различных количествах. При этом, обыкновенно, действующую массу выражают в виде концентрации, которая выражает количества вещества, выраженное в килограмм-молекулах, в одном кубическом метре. Вместо термина сила X. сродства употребляют термин скорость реакции, который выражает количество вещества, подвергающееся превращению в единицу времени, и принимают, что скорость реакции пропорциональна концентрации, если превращению подвергается одно тело, или же она пропорциональна произведению концентраций, если в реакции участвует несколько тел. Самый вывод уравнения равновесия может быть сделан двумя путями: кинетическим и термодинамическим, причем нужно иметь в виду, что все такие выводы приложимы лишь к случаям газообразного состояния или разведенных растворов, при которых имеет место уравнение: PV = RT. При кинетическом способе равновесие рассматривается как результат двух противоположных реакций, совершающихся с одинаковой скоростью. Скорость каждого превращения пропорциональна количеству превращающегося тела в единице объема, т. е. его концентрации, если в превращении участвует одна молекула; если же в реакции участвует несколько частиц, то скорость превращения будет пропорциональна числу ударов и столкновений частиц, участвующих в превращении, и это число при достаточном разведении пропорционально произведению концентраций. В частности, если взять, напр., реакцию образования сложных эфиров: спирт + кислота ↔ эфир + вода, то скорость первого превращения
(dCc)/(dt) = K1CaCs
скорость обратного превращения выразится равенством
(dCc)/(dt) = K2CcCw
отсюда условие равновесия получится в виде выражения: K1CaCs = K2CcCw
где K1 и K2, есть коэффициенты пропорциональности, a Ca, С s, С c и С w есть концентрации спирта, кислоты, эфира и воды в момент равновесия. При термодинамическом выводе уравнения равновесия превращение определенного количества вещества производят при помощи кругового процесса, дозволяющего вычислить работу каждой части превращения, и уравнение равновесия получают на основании того положения термодинамики, что сумма всех работ, совершенных при круговом процессе, при постоянной температуре, должна равняться нулю. Для примера рассмотрим равновесие, которое устанавливается при высокой температуре в системе, заключающей хлор, пары воды, хлористый водород и кислород. Равновесие в этой системе обуславливается двумя превращениями: с одной стороны, хлор и вода превращаются в хлористый водород и кислород, а с другой стороны, хлористый водород и кислород образуют воду и хлор, что и выражается следующим равенством:
2Cl2 + 2H2O ↔ 4ClH + O2.
Задача, следовательно, заключается в том, чтобы найти условие, при котором система, заключающая все четыре тела, будет находиться в состоянии равновесия. Для решения этой задачи предположим, что в двух пространствах, А и B, удерживаемых при постоянной температуре, находятся эти четыре тела, причем концентрации этих тел, а также и количества, после того как установилось равновесие, различны. Обозначим для А концентрацию этих тел символами С Cl2, С H2O, cO2 и CHCl, и для В — символами с Cl2, с H2O, cO2 и cHCl. Совершим превращение над количествами, отвечающими формулам 2Cl 2 + 2Н 2 О, при помощи кругового процесса. Осуществлено это может быть след. образом.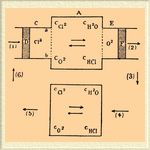
В цилиндре С мы имеем поршень D и перепонку ab, которая проницаема только для хлора. С помощью поршня D и полупроницаемой перепонки ab мы можем ввести в пространство А желаемое количество хлора. Подобным же образом затем мы введем и водяной пар, тогда как кислород и хлористый водород выведем из этого пространства, пользуясь цилиндром E поршнем F и соответственными полупроницаемыми перепонками. Если газы имеют ту же концентрацию, что и в A, то в А ничего не изменится, если произойдет образование кислорода и хлористого водорода, которые затем будут уведены. Теперь выведенные газы О 2 и НCl при той же температуре обратимым процессом будем сжимать или расширять до тех пор, пока не получим такой концентрации, которая имеет место в В, тогда, по предыдущему, произведем обратное превращение и, наконец, полученные продукты приведем к концентрациям, отвечающим А. Так как этот замкнутый цикл совершился при постоянной температуре, то сумма всех работ равна нулю. Следовательно:
(1) + (2) + (3) + (4) + (5) + (6) = 0.
Символ (1) выражает работу, затраченную для того, чтобы ввести хлор и воду; эта работа возвращается, когда эти газы выводятся, так как произведение PV при постоянной температуре для одного и того же количества газа есть величина постоянная. Следовательно
(1) + (5) = 0.
Точно так же и
(2) + (4) = 0,
а следовательно и
(3) + (6) = 0.
Таким образом сумма работ, произведенных при изменении концентрации, равна нулю. Для газов эта работа для килограмм-молекулы в калориях выразится формулой: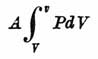
или выражая А при помощи уравнения
APV = 2T,
получим: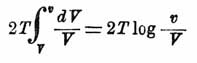
и так как концентрации обратно пропорциональны объему, то
2Tlog(v/V) = 2Tlog(C/c)
Таким образом для выражения (3) найдем
2TLg(CO2/cO2) + 4.2TLg(CHCl/cHCl)
и для выражения (6) получим
2.2TLg(cCl2/CCl2) + 2.2TLg(cH2O/CH2O).
Приравнивая сумму этих двух выражений нулю и произведя сокращение на 2 T, получим:
Lg(CO2/cO2) + 4Lg(CHCl/cHCl) + 2Lg(cCl2/CCl2) + 2Lg(cH2O/CH2O) = 0
Перенося члены, отвечающие пространству А в одну часть, а отвечающие пространству B — в другую, получим:
LgCO2 + 4LgCHCl — 2LgCCl2 — 2LgCH2O = Lgс O2 + 4LgcHCl — 2LgcCl2 — 2LgcH2O
Отсюда видно, что некоторая функция от концентрации есть величина постоянная. Эта функция получается, если помножить логарифмы концентраций каждого тела на число частиц его, участвующих в равновесии, причем члены, отвечающие одному превращению, входят с положительным знаком, а обратному — с отрицательным. Таким образом в общей форме уравнение равновесия примет следующий вид:
Σ nLg C = Const.
где n представляет число молекул каждого тела, а С концентрации их. Выражение это может быть представлено в другой форме, а именно: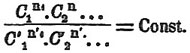
Частным случаем этого выражения является выражение этого закона, данное Гульдбергом и Вааге.
Проверка закона действия масс опытным путем возможна двумя способами: статическим и динамическим. Первый способ заключается в том, что изменяют действующие массы тел и, пользуясь выведенным уравнением, вычисляют, как должен измениться предел реакции. При втором способе определяют количество превращенного вещества до наступления равновесия через определенное время после начала реакции и из полученных данных определяют константу, которая выразится как функция концентрации и времени и которая должна сохранять постоянную величину через различные промежутки времени. Чтобы показать, как применяются эти способы, приведем два примера. Известно, что йодистый водород при нагревании разлагается на водород и йод: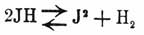
превращение это не идет до конца, так как йод и водород обратно соединяются и дают йодистый водород. Таким образом здесь наступает химическое равновесие, причем в системе одновременно существуют все три тела. Предел этого превращения при постоянной температуре должен зависеть от действующих масс или концентраций этих тел. Применяя к этому случаю общее уравнение равновесия, получим:
LgС J2 + LgС H2 — 2Lgchj = Const.,
или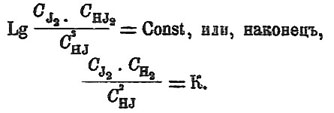
Обозначим через 1 начальное количество водорода (в молекулах), через α начальное количество йода; вследствие реакции образуется 2 γ молекул йодистого водорода. Следовательно, когда наступит равновесие, система будет заключать 2 γ молекул HJ, 1 — γ молекул водорода и α — γ молекул йода. Подставляя эти величины в наше уравнение, получим:
[(1 — γ)(α — γ)]/[4 γ 2] = K,
откуда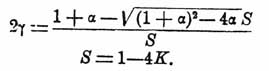
где
S = 1 — 4K.
Если изменять величину α (количество йода), то величина 2γ будет изменяться, и это изменение может быть определено прямым опытом. В нижеследующей таблице приведены данные, относящиеся к 440°С, которые дают эту величину опытную и вычисленную для различных количеств йода; количества водорода, йода и йодистого водорода даны в куб. см, отнесенных к 0°С и 760 мм давления:
| H2 | J2 | J2/H2 = a | HJ опыт. | 2 γ выч. |
| 20,57 | 5,22 | 0,254 | 10,22 | 10,19 |
| 20,6 | 14,45 | 0,702 | 25,72 | 25,54 |
| 20,53 | 25,42 | 1,238 | 34,72 | 34,96 |
| 20,55 | 31,89 | 1,552 | 36,98 | 37,13 |
| 20,41 | 52,80 | 2,538 | 38,68 | 39,01 |
| 20,28 | 67,24 | 3,316 | 39,52 | 39,25 |
| 19,99 | 100,98 | 5,048 | 39,62 | 39,22 |
Последние два столбца в этой таблице показывают, что опыт и вычисление приводят к согласным результатам, и подтверждают справедливость уравнения равновесия. В качестве второго примера мы возьмем действие едкого натра на монохлоруксусно-кислый натрий:
C2H2ClO2Na + NaOH = C2H3O3Na + NaCl.
Реакция эта совершается при 100°С в водном растворе в продолжение 24 часов, и хотя при этих условиях она не обратима и не приводит к X. равновесию, но для нашей цели интересна в том отношении, что показывает справедливость основного закона, что скорость реакции пропорциональна произведению действующих масс; самый опыт производится таким образом, что через определенные промежутки времени определяется титр жидкости, причем между концентрацией действующих масс и титром жидкости существует простое соотношение:
Cn/Tn = C1/T1
где Cn и C1 — концентрации в конце и в начале, а Tn и T1 — титр конечный и начальный жидкости. Согласно закону масс скорость реакции, т. е. скорость исчезновения взятых для реакции тел, выразится следующим образом:
— dC/dt = kC1C2 = kC2
Интегрируя это уравнение, получим:
1/C = kt + Const.
Исключая Const при помощи соотношения
1/C1= Const
и выражая С n через величины Т 1 и Т n пользуясь выше приведенным соотношением, для величины k получаем выражение:
k = [1/(tC1)][(T1 — Tn)/Tn].
Величина эта должна остаться постоянной при изменении t, что вполне подтверждают нижеследующие данные:
| Время в минутах t | Титр жидкости Tn | k |
| 13 | 14,1 | 0,15 |
| 23 | 13,3 | 0,15 |
| 33 | 12,75 | 0,138 |
| 63 | 11,15 | 0,136 |
| 93 | 10 | 0,131 |
| 123 | 8,95 | 0,133 |
| 153 | 8 | 0,138 |
| 183 | 7,3 | 0,138 |
| 258 | 5,95 | 0,141 |
| 318 | 5,15 | 0,144 |
| 378 | 4,55 | 0,145 |
Не останавливаясь на других примерах и доказательствах закона действия массы, укажем только, что строгое применение его к вычислению возможно только в тех случаях, где реакция не нарушается никакими осложняющими явлениями, вот почему наиболее благоприятными случаями для проверки этого закона являются газы и разбавленные растворы, в которых изменение среды вследствие реакции настолько ничтожно, что им можно пренебречь. В тех случаях, где изменение среды достигает значительных размеров, в уравнение равновесия и скорости нужно вводить добавочные члены, что в большинстве случаев представляет большую трудность, а часто даже и невозможно.
Рассмотренные нами до сих пор случаи относились к X. равновесию в однородной среде, т. е. когда имеется только одна фаза. Но этот же закон имеет место и по отношению в равновесию в неоднородной среде, т. е. когда в реакции участвуют две или более фаз. В этом случае условия достижения равновесной системы более ограничены, так как существование ее требует не только того, чтобы в каждой фазе тела находились в равновесии, но и чтобы фазы между собой находились в равновесии. Поэтому при данных условиях температуры и давления из всех возможных для каждой фазы состояний равновесия одновременно могут существовать только некоторые. Правила и законы, сюда относящиеся, формулируются так называемым правилом фаз (см.). Применение закона действия масс во многих частных случаях значительно облегчается. Таковы, напр., случаи диссоциации твердого тела, когда продукты диссоциации являются телами газообразными. Применение закона действия массы в этих случаях крайне просто, потому что действующая масса твердого тела есть величина постоянная. Это положение вытекает из того соображения, что X. взаимодействие совершается только на поверхности твердого тела, а так как оно должно зависеть от концентраций действующих тел — а концентрация твердого тела остается неизменной — то на состояние равновесия может влиять только изменение концентрации газообразных тел. Поэтому основное уравнение равновесия: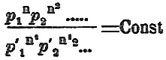
превращается в более простое уравнение: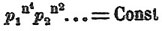
т. е. произведение парциальных давлений, показатели степеней которых равны числу частиц, участвующих в реакции, — величина постоянная. Так, если диссоциация сопровождается образованием одного продукта диссоциации, то условие равновесия будет такое: p = Const., т. е. упругость диссоциации есть величина постоянная, такой случай мы имеем при диссоциации углекислого кальция СаСО 3, при диссоциации кристаллогидратов и т. п. В случае, если продуктов диссоциации несколько, то условие равновесия будет заключаться в постоянстве произведения парциальных давлений, возведенных в соответственные степени; таковы, напр., случаи разложения NH 4 SH и CO(NH 2)ONH4, изученные Горстманом. Диссоциация первого тела происходит по уравнению:
NH4SH = NH3 + H2S
и уравнение равновесия для него будет
р 1.р 2 = Const.
Диссоциация второго тела совершается согласно уравнению:
CO(NH2)ONH2 = CO2 + 2NH3
и для него уравнение равновесия имеет вид:
p1.р 22 = Const.
Справедливость обоих этих уравнений была подтверждена исследованиями Горстмана, определившего парциальные давления продуктов диссоциации этих тел в присутствии избытка одного из продуктов диссоциации. Необходимо при этом иметь в виду, что все вышеприведенные рассуждения справедливы только до тех пор, пока имеет место основное положение о постоянстве действующей массы твердого тела, т. е. до тех пор, пока при диссоциации само твердое тело своих свойств не меняет. Но как только этого нет, то все вышеприведенные правильности уже не применимы в той форме, как это было сделано для разобранных случаев, и тогда уравнение равновесия принимает совершенно другой вид. Это, напр., имеет место в тех случаях, когда твердое тело с продуктами своей диссоциации образует твердые растворы, тогда концентрация твердого тела, а следовательно, и его действующая масса изменяется при изменении концентрации газообразных продуктов, и для таких систем уже не имеет места постоянство произведений парциальных давлений. К случаям такого рода относится, напр., диссоциация водородистого палладия, при которой упругость водорода не остается постоянной при данной температуре, но все время изменяется. Подробности — см. Диссоциация.
Перейдем теперь к рассмотрению вопроса о том, как изменяется состояние равновесия при изменении температуры и давления. Как известно, в этом отношении мы имеем общий закон Ле-Шателье — Вант-Гоффа, согласно которому при изменении температуры и давления в системе развиваются процессы, сопротивляющиеся этим изменениям, т. е. при повышении температуры предел перемещается в том направлении, при котором происходит поглощение теплоты, а при увеличении давления в системе совершаются процессы, сопровождаемые сжатием, и наоборот. Не останавливаясь на качественной проверке этого закона (см. Правило фаз, обратимость химических реакций), мы здесь рассмотрим только количественную сторону.
2) Влияние температуры. В общем уравнении равновесия:
Σ nLgC = Κ
величина K остается постоянной, пока температура остается неизменной. Но с изменением температуры К изменяется, и закон этого изменения можно вывести при помощи термодинамики. Не приводя самого вывода, дадим только окончательный результат:
(dK)/(dT) = q/(2T2),
где q есть теплота, выделяемая при превращении одной грамм-молекулы той системы, которая превращается с выделением теплоты. Это выражение, показывая справедливость общего закона, позволяет делать даже и количественные выводы. Из него также прямо вытекает, что если
q = 0, то (dK)/(dT) = 0,
т. е. изменение температуры не изменяет состояния равновесия. Подобный случай имеет место при этерификации: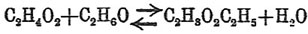
Это превращение сопровождается крайне незначительным тепловым эффектом, и в связи с этим оказывается, что температура почти не влияет на него: при 10°С предел реакции наступает, когда превращению подвергнутся 65,2% смеси кислоты и спирта, а при 220° этот предел = 66,5%.
Для некоторых частных случаев влияние температуры на изменение равновесия может быть выведено при помощи уравнения Клапейрона. Рассмотрим, напр., диссоциацию кристаллогидрата Na 2HPO4.12H2 О. Возьмем уравнение Клапейрона:
AVdP = q(dT/T),
где А = 1/425, V изменение объема при превращении, q теплота испарения грамм-молекулы воды из кристаллогидрата. Пользуясь уравнением:
APV = 2T,
преобразуем его так, чтобы исключить V, тогда получим: (dP)/P = q [(dT)/(dT2).
Интегрируя это уравнение, принимая, что q не зависит от температуры, получим
Lgp = — q/(2T) + Const
и в окончательном виде
Lgp = — q/(4,6T) + Const = В — A/T,
где В и А — постоянные величины. Полученное выражение показывает, как изменяется упругость диссоциации с температурой. Для определения постоянных А и B достаточно двух наблюдений при разных температурах над упругостью диссоциации. Она была определена при 6,8°С и 27°С. В нижеследующей таблице приведены значения для Р, наблюденные при разных температурах и вычисленные с помощью полученного уравнения; из этой таблицы видно, что теория и опыт приводят к совершенно согласным результатам:
| Температура | Ρ набдюден. | Ρ вычисл. |
| 6,80° | 4,606 | (4,606) |
| 10,82° | 6,382 | 6.386 |
| 15,00° | 8,837 | 8,85 |
| 17,28° | 10,531 | 10,55 |
| 20,15° | 13,087 | 13,093 |
| 23,02° | 16,191 | 16,184 |
| 27,00° | 21,575 | (21,575) |
Числа, в скобках, послужили для вычисления постоянных уравнений. Заметим еще, что это же уравнение может служить для вычисления q, так как А= q/4,6 откуда для q найдем 12817 кал., число вполне подтверждается непосредственными калориметрическими опытами. Таким образом, термодинамика дает возможность не только находить зависимость между упругостью диссоциации и температурой, но и позволяет вычислить, на основании упругости диссоциации, теплоту превращения.
3) Влияние давления. Влияние давления на изменения X. равновесия может быть выведено на основании того простого соотношения, которое существует между концентрацией и объемом. Не приводя самого вывода, заметим только, что оно дает возможность точно так же предвидеть не только качественно, но и количественно перемещение равновесия под влиянием давления. При этом, так же как и при изменении температуры, как следствие из общего уравнения, мы получим положение, что на реакции, не сопровождаемые изменением объема, давление не оказывает никакого влияния, что вполне подтверждается непосредственными наблюдениями. Чтобы показать применение формул термодинамики, разберем один частный случай, а именно, изменение температуры перехода ромбической серы в одноклиномерную. При обыкновенном давлении точка перехода лежит при 95,6°, давление должно изменять температуру перехода, и для вычисления этого изменения может служить формула Клаузиуса:
[dT]/[dP] = 10333.([T(σ — τ)]/[425q]),
где q есть теплота превращения, a σ и τ удельные объемы двух разновидностей серы. Теория и опыт и в этом случае приводят к полному согласию, показывая, что увеличение давления на одну атмосферу повышает точку перехода на 0,05°С.
В заключение настоящей статьи укажем, что общая теория X. равновесий может быть выведена на основании начал термодинамики, причем в уравнение, определяющее состояние системы, войдут: абсолютная температура T, давление Р, внутренняя энергия U, объем V и энтропия S. Зависимость между этими величинами дается уравнением:
TdS = dU + PdV.
Анализ этого уравнения — принимая за независимые переменные Т и V — приводит к двум новым уравнениям:
dS/dT = 1/T[dU/dT]
и
dS/dV = 1/T[(dU/dV) + P]
Из последнего уравнения можно определить
P = — [d(U — TS)]/[dV],
или обозначая (U — TS) через F, получим:
P = — (dF)/(dV).
Величину
f = U — TS
Гельмгольц назвал свободной энергией, и эту же величину (при постоянном объеме) Дюгем назвал термодинамическим потенциалом. Учение о свободной энергии и термодинамическом потенциале дает возможность изучать случаи X. равновесия, не прибегая ни к каким гипотезам и допущениям и оставаясь на почве только термодинамических соотношений.
А. Байков.
| "БРОКГАУЗ И ЕФРОН" >> "Х" >> "ХИ" >> "ХИМ" |
Статья про "Химические равновесия" в словаре Брокгауза и Ефрона была прочитана 1907 раз
| Семга на горелке |
| Семга на горелке |
TOP 15
- Волос
- Проно
- Степные животные
- Гимнастика
- Индийский океан
- Архитектура
- Сравнение, в литературе
- Манда
- Клитры
- Колесование
- Испарение
- Травоядные животные
- Оплодотворение у pacтений
- Вредные насекомые
- Электризация тел