


БНБ
"БРОКГАУЗ И ЕФРОН" (121188)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Упругость твердых тел
Определение "Упругость твердых тел" в словаре Брокгауза и Ефрона
Упругость твердых тел — свойство твердых тел восстановлять свою форму при прекращении действия сил, изменяющих форму или размеры тел, если силы эти не превосходят тех пределов, за которыми восстановление формы тела совершается не вполне, так что остаются некоторые деформации, не исчезающие после прекращения действия сил. Учение о равновесии и движении тел, называемое теорией У., составляет, вместе с гидродинамикою, механику сплошных деформируемых тел. О деформациях сплошных тел говорится в статье Деформация. Там уже было сказано, что в теории У. рассматриваются деформации, при которых вокруг каждой точки тела, в ближайшем соседстве ее, относительные деформации однородны и ничтожно малы. Если x, у, z суть координаты какой-либо точки тела до деформации, а х + u, y + v, z + w — координаты той же точки при деформации, то величины u, v, w суть проекции на оси координат перемещения точки. Величины эти будут функциями от x, у, z. Для того, чтобы вполне знать перемещения всех частей тела, надо знать, какие это функции. Проекции перемещения другой точки, отстоящей от первой на весьма малое расстояние и координаты которой до деформации суть x + Δ x, у + Δ y, z + Δ z, будут отличаться от u, v, w на величины: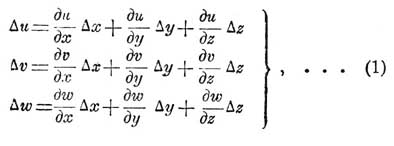
пренебрегая членами, заключающими квадраты и высшие степени величин Δ x, Δ y, Δ z. Сравнив эти равенства с равенствами (F) статьи Деформация, мы видим, что в соседстве каждой точки происходит однородная относительная деформация, предположение же о ничтожной малости ее можно выразить требованием, чтобы Δ u, Δ v, Δ w были ничтожно малы сравнительно с величинами Δ x, Δ y, Δ z; для этого необходимо, чтобы все девять производных, входящие во вторые части равенств (1), были бы ничтожно малыми величинами; тогда в выражениях, заключающих различные степени этих величин, мы имеем право пренебречь членами, заключающими высшие степени этих производных, и должны сохранить только члены с низшею степенью их. Элемент объема, имеющий вид прямоугольного параллелепипеда, ребра которого суть Δ x, Δ y, Δ z, параллельные соответственным осям координат, при однородной деформации обращается в косоугольный параллелепипед, причем ребра получают следующие удлинения на единицу длины:
ε 1 = (дu)/(дх); ε 2 = (дv)/(дy); ε 3 = (дw)/(дz);
первое — удлинение ребер Δ x, второе — ребер Δ y, третье — ребер Δ z. Прямые углы между ребрами прямоугольного параллелепипеда при деформации скашиваются, т. е. перестают быть прямыми. Такое скашивание обуславливается образованием сдвигов при деформации (см. Деформация, Сопрот. материалов). Величина двойного сдвига в плоскости ΥΖ измеряется половиною косинуса угла между направлениями, которые получат ребра Δ y, Δ z после деформации: величина эта выражается так
g1 = 1/2[(дv)/(дz) + (дw)/(дy)]
и называется величиною сдвига в плоскости YZ; подобным образом величины сдвигов в плоскостях ZX и XY выражаются так:
g2 = 1/2[(дw)/(дx) + (дu)/(дz)]
g3 = 1/2[(дu)/(дy) + (дv)/(дx)]
Кубическое расширение (на единицу объема) при деформации измеряется величиною
q = ε 1 + ε 2 + ε 3
Твердое тело, по-видимому, сплошное, состоит, однако, из отдельных молекул, число которых даже в весьма малом элементе огромно. Между молекулами действуют молекулярные силы, подчиняющиеся закону взаимодействия (см.). В статье Напряжение (см.) дано понятие о том, что называется напряжением, действующим на какую-либо площадку. Здесь придется сказать об этом несколько подробнее. Молекулярные силы, действующие между каждою парою молекул, имеют заметную величину только тогда, когда расстояние между ними не превосходит малой величины, называемой радиусом молекулярного взаимодействия. Вследствие этого при рассуждениях относительно напряжений, действующих на какую-либо малую площадку, проведенную где-либо в теле, приходится принимать во внимание только взаимодействия между молекулами, находящимися близ площадки и отстоящими от неё не далее радиуса взаимодействий. Для того, чтобы отличить обе стороны площадки, мы восстановим из середины ее нормаль в одну сторону, и эту сторону площадки назовем переднею, а другую — заднею. Совокупность молекулярных сил, действующих сквозь площадку со стороны молекул, находящихся около задней стороны, на молекулы, находящиеся около передней стороны, есть напряжение, которое мы считаем приложенным к площадке; мы представляем себе его в виде силы, имеющей величину и направление. Если величина площадки равна ω, то величину напряжения означим через F ω, так что F есть величина напряжения, приходящегося на единицу поверхности площадки. Совокупность напряжений от молекул, находящихся с передней стороны, на молекулы, находящиеся с задней стороны, равна и противоположна F ω вследствие начала равенства и противоположности взаимодействий. Проекции F на оси координат мы означим через Хn, Уn, Zn. Когда к телу не приложено никаких внешних сил, ни давлений на его поверхность, то тело находится в естественном, недеформированном состоянии и напряжения на всякую площадку равны нулю. При действии сил и давлений на поверхность тела в нем являются деформации и развиваются напряжения, различные для различных точек тела и площадок, через них проведенных. В одной и той же точке величины Хn, Уn, Zn различны для различных направлений n; так что эти величины суть функции от пяти величин, а именно от трех координат x, у, z той точки тела, через которую проведена площадка, и от двух углов, определяющих направление нормали n к этой площадке. Гук (Robert Hooke) открыл, что напряжения пропорциональны деформациям; это положение служит теперь основным началом в теории упругости, и в силу его Хn, Уn, Zn должны быть линейными выражениями вида
а ε 1 + b ε 2 + с ε 3 + еg1 + hg2 + fg3
относительно шести величин, выражающих деформацию. Напряжения, действующие на площадки, проходящие через одну и ту же точку тела, но различно ориентированные, находятся в некоторой зависимости между собою. Рассматривая условия равновесия элемента объема, имеющего вид бесконечно малого тетраэдра, три грани которого перпендикулярны к осям координат, а нормаль четвертой имеет какое-либо направление n, можно показать следующее: проекция на ось Y-ов напряжения, приложенного к площадке, перпендикулярной к оси Z-ов, равна проекции на ось Z-ов напряжения, приложенного к площадке, перпендикулярной к оси Y-ов. По нашему условному обозначению, это можно выразить так: Yz = Ζ y. Эти равные между собою величины мы означим через T1; точно так же окажется, что Ζ x = Χ z, эти равные величины означим через T2, а через Т3 значим две тоже равные величины Ху = Yx. Таким образом, мы вводим в наши соображения площадки, имеющие нормалями направления, параллельные осям координат, и напряжения, к ним приложенные. Условимся обозначать особыми знаками нормальные составляющие напряжений на такие площадки; так, N1 будет Xx, т. е. проекция на ось Х-ов напряжения, действующего на площадку, имеющую нормаль, параллельную положительному направлению этой оси; подобно этому N2 означает Yу и N3 означает Zz. Кроме того, из уравнений равновесия того же тетраэдра окажется, что существуют следующие зависимости: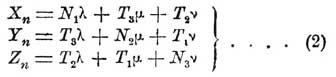
где λ, μ, ν — суть косинусы углов, составляемых направлением нормали n с направлениями положительных осей Х-ов, Y-ов и Z-ов. Таким же равенствам (2) подчиняются напряжения внешних сил, приложенных к элементам наружной поверхности тела; эти наружные напряжения тоже рассчитываются на единицу поверхности. Они уравновешиваются с молекулярными напряжениями, приложенными к задним сторонам элементов поверхности. Нормали к этим элементам считаются проведенными внаружу тела. Кроме наружных напряжений, приложенных к наружной поверхности тела, к нему могут быть приложены еще так называемые объемные силы, приложенные ко всем точкам объема тела; таковы, напр., силы тяжести. Такие объемные силы рассчитываются на единицу массы. Проекции этих сил (действующих на единицу массы) на оси координат мы означим так: Χ, Y, Ζ. Если σ есть плотность вещества тела, то элемент объема, имеющий вид параллелепипеда, ребра которого, параллельные осям координат, имеют величины дх, ду, дz, будет иметь массу σ дхдудz, а проекции на оси координат объемных сил, действующих на этот элемент, будут равны произведениям из величин Χ, Y, Ζ на величину массы элемента. Дифференциальные уравнения движения точек упругого тела могут быть получены из дифференциальных уравнений движения центра инерции вышесказанного элемента объема. Они имеют следующий вид: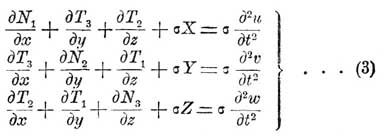
Они могут быть получены, и при том еще вместе с равенствами (2), из начала д'Аламбера, т. е., вернее сказать, из уравнения, выражающего, что работа потерянных сил при виртуальных перемещениях равна нулю. Уравнение это для какой-либо системы материальных точек имеет такой вид:
Σ ([X — m(д2x)/(дt2)] δ x + [Y — m(д2y)/(дt2)] δ y + [Z — m(д2z)/(дt2)] δ z) = 0
При применении к упругому телу, в этом уравнении надо заменить: δ x, δ y, δ z — величинами δ u, δ v, δ w, x, y, z — величинами u, v, w, массу т величиною массы элемента, а проекции приложенных сил — проекциями объемных сил и внешних напряжений, действующих на поверхность тела; кроме того, к первой части уравнения надо еще присоединить виртуальную работу молекулярных сил. Суммирование должно быть заменено интегралом по всему объему тела. Так как по закону Гука напряжения зависят от деформаций, то и потенциал молекулярных сил элемента объема (дхдудz) должен быть функциею величин ε 1, ε 2, ε 3, g1, g2, g3, определяющих деформацию. Ввиду этого Грин (George Green) предположил, что потенциал молекулярных работ всего тела выражается интегралом по всему объему: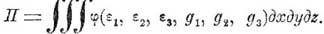
Когда силы имеют потенциал, то виртуальная работа таких сил выражается вариациею потенциала, поэтому виртуальная работа всех молекулярных сил будет равна δ П. Вследствие малости деформаций, можно, разложив функцию φ в ряд по возрастающим степеням величин ε 1, ε 2, ε 3, g1, g2, g3, пренебречь членами ряда, заключающими степени этих величин выше второй. Поступив таким образом, можно из уравнения (4) получить и дифференциальные уравнения (3) и уравнения (2), причем окажется, что напряжения N1, N2, N3 Т1, Т2, T3 выражаются шестичленами, каждый из которых состоит из членов равных произведениям одной из величин ε 1, ε 2, ε 3, g1, g2, g3 на некоторый численный коэффициент. Коэффициенты эти называются коэффициентами У. и число их равно 21. Таков метод Грина для получения зависимости между напряжениями и деформациями. Если строение тела имеет три взаимно-перпендикулярные плоскости симметрии, то число коэффициентов У. уменьшается до девяти. Если вещество обладает полною изотропиею, т. е. строение его по всем возможным направлениям, проведенным из любой точки тела, одинаково, то число коэффициентов У. равно двум; тогда функция φ имеет вид:
2 φ = Β q2 + 2G (ε 12 + ε 22 + ε 32 + 2g12 + 2g22 + g32)... (5)
а выражения шести напряжений таковы: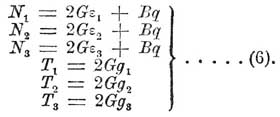
Для объяснения значения этих двух коэффициентов мы рассмотрим следующие случаи:
1) Твердое тело, имеющее какую-либо форму, деформируется таким образом, что
и = ах, v = ay, w = az
тогда ε 1= ε 2= ε 3=а и все три сдвига равны нулю. Значит, линейное расширение по всем направлениям одно и то же и поверхность тела остается подобною первоначальному виду. Кубическое расширение единицы объема q равно 3a. По формулам (6):
N1 = N2 = N3 = (2G + 3B)a
T1 = T2 = T3 = 0.
Если тело не подвержено никаким объемным силам и остается в покое, так что u, v, w от t не зависят, то уравнения (3) будут удовлетворены. Из уравнения же (2) следует, что тогда приложенные к поверхности напряжения должны быть натяжениями, нормальными к поверхности, и величина натяжения P на ед. поверхности должна быть равна N1 = N2 = N3. Отсюда мы видим, что изотропное тело, растягиваемое равномерно распределенным по его поверхности натяжением, расширяется одинаково по всем направлениям и получает на каждую единицу объема куб. расширение [P:(2/3G+B )]. При равномерно распределенном по поверхности давлении P (на един. поверхн.) получается на каждую единицу объема такое же кубическое сжатие. Отношение P к q, т. е. к 3а, называется модулем сжимаемости. Таким образом, 2/3G+B есть модуль сжимаемости.
2) Предположим, что тело деформируется так:
u = 0, v = bx, w = 0,
тогда ε 1 = ε 2 = ε 3 = q1 = 0, g1 = 0, g2 = 0, 2g3 = b. Тело совершает простой сдвиг параллельно оси Y-ов, причем грань, заключающаяся в плоскости YZ, остается неподвижною, а все плоскости, ей параллельные, сдвигаются параллельно оси Y-ов на расстояния, пропорциональные x, причем плоскость, отстоящая на расстояние, равное единице, сдвигается на длину b. По формулам (6) окажется, что только T3 = Gb, a остальные пять напряжений равны нулю. При отсутствии объемных сил и равновесии тела такие напряжения удовлетворяют уравнениям (3). Положим, что тело имеет вид пласта, одна поверхность которого заключается в плоскости YZ и закреплена в ней, другая параллельна этой плоскости, и толщина пласта по оси Х-ов равна единице. Чтобы весь пласт испытал вышесказанный сдвиг, надо к каждой единице второй поверхности приложить тангенциальное напряжение, параллельное оси Y-ов и равное Т3 = Gb. Отношение тангенциального напряжения к величине сдвига называется модулем твердости. Следовательно, G есть модуль твердости.
3) Предположим, что твердое тело имеет вид призмы квадратного сечения, длина которой имеет направление оси Х-ов, стороны квадратов оснований равны единице и параллельны оси Y-ов и оси Z-ов. Тело деформируется так:
и = ах, v = су, w = сz;
поэтому ε 1 = a, ε 2 = ε 3 = с, q = а + 2с, все g1, g2, g3 равны нулю. По формулам (6) все три Т равны нулю, затем
N1 = 2Ga + B(a + 2c).
N2 = N3 = 2Gc + B(a + 2с).
При отсутствии объемных сил и при равновесии тела эти напряжения удовлетворяют уравнениям (3). Из уравнений (2) окажется, что все грани призмы должны подвергаться нормальным напряжениям. Положим, что боковые грани не подвержены вовсе никаким силам, а к основаниям приложены натяжения Р, тогда a и с должны удовлетворять двум равенствам:
P = 2Ga + B(a + 2c)
0 = 2Ge + B(a + 2с).
Второе из них может послужить для определения отношения:
c/a = — B/[2(G + B)];
вычтя же из первого равенства второе, получим
Р = 2G(а — с).
Так как В и G суть величины положительные, то отношение с:а есть величина отрицательная; продольное растяжение сопровождается поперечным сжатием. Означим это отношение через (— μ .). Тогда
Ρ = 2(1 + μ)Ga;
Β (1 — 2 μ) = 2G μ .
Отношение Р к a, как известно, называется Юнговым модулем или модулем У. Означив его через E, найдем, что оба коэффициента G и В выражаются через модуль У. и через величину отношения поперечного сжатия к продольному растяжению след. образом:
G = E/[2(1 + μ)]; B = E μ /[(1 — 2 μ)(1 + μ)].
Краткая история развития теории У. приведена в статье Сопротивление материалов. Наиболее полную и подробную историю этого предмета представляет книга Тодгентера: "A history of the theory of elasticity", дополненная и изданная проф. Pearson (первый том в 1886 г., две части второго — в 1893 г., Cambridge, University Press). Хотя первыми вопросами по сопротивлению балок занимался еще Галилей, но настоящая теория У. началась и стала развиваться преимущественно с 20-х годов XIX стол. Несмотря на такое сравнительно недавнее происхождение, теория У. послужила к решению весьма многих вопросов, напр. о равновесии и колебаниях стержней, пластин, прямых и искривленных, об изгибе и кручении призм, о распространении волнообразных колебаний в упругой среде и проч. В настоящее время имеется весьма большое число трактатов по теории У. Укажем на некоторые из них: Lam é, "Le ç ons sur la theorie math é matique de l' é lasticit é des corps solides" (1862); Clebcsh, "Theorie der Elasticit ä t fester K ö rper" (1862); "Th é orie de l' é lasticit é des corps solides de Clebsch, traduite par Barr é de Saint-Venant et Flamant" (1883); Franz Neumann, "Vorlesungen ü ber die Theorie der Elasticit ä t der festen K ö rper und des Licht ä thers" (1885); Weyrauch, "Theorie elastischer K ö rper" (1884); W. J. Jbbetson, "An elementary treatise on the mathematical theory of perfectly elastic solids", (1887).
Д. Б.
| "БРОКГАУЗ И ЕФРОН" >> "У" >> "УП" |
Статья про "Упругость твердых тел" в словаре Брокгауза и Ефрона была прочитана 1310 раз
| Коптим скумбрию в коробке |
| Гороховое пюре |
TOP 15
- Волос
- Проно
- Степные животные
- Гимнастика
- Индийский океан
- Архитектура
- Сравнение, в литературе
- Манда
- Клитры
- Колесование
- Испарение
- Травоядные животные
- Оплодотворение у pacтений
- Вредные насекомые
- Электризация тел