


БНБ
"БРОКГАУЗ И ЕФРОН" (121188)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Ультраэллиптические интегралы и функции
Определение "Ультраэллиптические интегралы и функции" в словаре Брокгауза и Ефрона
Ультраэллиптические интегралы и функции — Квадратуры вида: 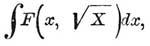 , где Χ есть целый полином степени выше четвертой относительно x, a F — какая-либо рациональная функция от x и √x называются У. или гиперэллиптическими интегралами.
, где Χ есть целый полином степени выше четвертой относительно x, a F — какая-либо рациональная функция от x и √x называются У. или гиперэллиптическими интегралами.
Теорией У. интегралов занимались Абель, Якоби, Гёпель, Розенгайн, Эрмит, Вейерштрассе, Прим, Нейман, Клебш и Гордан, Г. Вебер, Томэ, Брио, Кенигсбергер и др.; у нас, в России, К. А. Поссе, П. М. Покровский, М. А. Тихомандрицкий и др.
Если Χ есть полином 5-й-или 6-й степени, то интегралы называются У. первого класса. С помощью подстановки:
x = (a + by)/(c + fy)
всегда возможно интеграл с полиномом Χ шестой степени относительно x привести к интегралу с полиномом Y пятой степени относительно у.
Те У. интегралы первого класса, которые могут быть приведены к виду: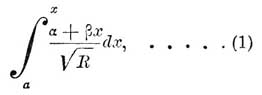
где R = x(1 — x)(1 — χ 2x)(1 — λ 2x)(1 — μ 2x), а величины a, α, β, χ , λ, μ — постоянные, называются ультраэллиптическими интегралами первого класса и первого рода. Они конечны для всех значений переменной х.
Если интеграл 1-го класса приводится к виду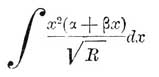
то он называется ультраэллиптическим интегралом второго рода. Он обращается в бесконечность алгебраически при х = ∞. Интеграл, приводящийся к виду: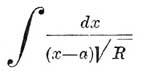
называется ультраэллиптическим интегралом третьего рода; он обращается в бесконечность логарифмически при x=a.
Начало теории ультраэллиптических интегралов было положено в 30-х годах прошлого XIX стол. знаменитою теоремою Абеля о сложении интегралов алгебраических функций. Из этой теоремы между прочим следует, что если имеем систему уравнений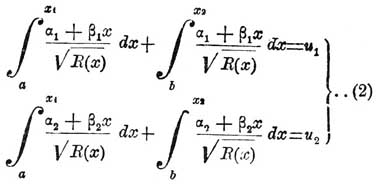
то х1 и x2, как функции от u1 и и2 суть корни квадратного уравнения:
Nx2 + mx + L = 0,
в котором N, М и L суть однозначные функции от и1 и и2.
Якоби показал, что L, M и N суть однозначные функции с четырьмя системами периодов, т. е. что они остаются без изменения, если одновременно заменим и1 и и2 через
и1 + n1A1 + n2B1 + n3C1 + n4D1
и2 + n1A2 + n2B2 + n3C2 + n4D2
где п1, п2, п3, п4 суть какие-либо целые числа, a A1, В1,С1, D1 и А2, В2, С2, D2 периоды двух интегралов в равенствах (2).
Требовалось определить те функции от и1 и и2, которые выражали бы х1 и x2 и соответствующие им значения √R(x1) и √R(x2), удовлетворяющие уравнениям (2).
Эта задача была решена почти одновременно Гёпелем и Розенгайном, которые показали, что для решения ее надо ввести особые функции от двух переменных, названный функциями Θ (тета) от двух аргументов; начало теории таких функций положил Риман.
Функция Θ от двух аргументов и1 и и2 выражается двойным бесконечным рядом.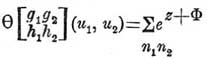
где:
z = 2(n1 + g1/2)(u1 +[h1/2] π i) + 2(n2 + g2/2)(u2 + [h2/2] π i)
Ф = (n1 + g1/2)2 τ 11 + 2(n1 + g1/2)(n2 + g2/2) τ 12 + (n2 + g2/2)2 τ 22
и где, в сумме, целые числа п1 имеют всевозможные величины от —∞ до +∞ и целые числа п2 имеют всевозможные величины от —∞ до +∞. Величины g1, g2, h1, h3, τ 11, τ 12, τ 22 суть постоянные.
Совокупность постоянных g1, g2, h1, h2 называется характеристикою функций Θ. При исследовании свойств этих функций оказывается, что существует только 16 различных функций Θ, а именно соответствующих характеристикам: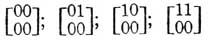
и т. д., при которых g1, g2, h1, h2 суть либо нули, либо единицы.
Функция Θ с характеристикой 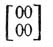 обозначается просто через Θ (u1u2).
обозначается просто через Θ (u1u2).
По изучении свойств этих функций Θ оказалось, что х1 и x2, а также √R(x1) и √R(x2) выражаются рационально в функциях Θ от двух аргументов и1 и u2.
Для знакомства с теориею ультраэллиптических интегралов и функций Θ от двух аргументов нужно обратиться к статьям и сочинениям вышеупомянутых ученых.
Д. Б.
| "БРОКГАУЗ И ЕФРОН" >> "У" >> "УЛ" >> "УЛЬ" |
Статья про "Ультраэллиптические интегралы и функции" в словаре Брокгауза и Ефрона была прочитана 804 раз
| Коптим скумбрию в коробке |
| Гороховое пюре |
TOP 15
- Волос
- Проно
- Степные животные
- Гимнастика
- Индийский океан
- Архитектура
- Сравнение, в литературе
- Манда
- Клитры
- Колесование
- Испарение
- Травоядные животные
- Оплодотворение у pacтений
- Вредные насекомые
- Электризация тел