


БНБ
"БРОКГАУЗ И ЕФРОН" (121188)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Тригональная система
Определение "Тригональная система" в словаре Брокгауза и Ефрона
Тригональная система
Тригональная система*
— одна из кристаллографических систем, характерный признак всех классов которой — присутствие одной тройной оси симметрии (или шестерной оси сложной симметрии), т. е. способность кристаллов принимать прежнее положение в пространстве при повороте на 120° вокруг этой оси. Некоторые классы этой системы стоят в очень близкой связи с гексагональной системой, с которой она и соединялась прежде и только недавно стала рассматриваться как самостоятельная система. В зависимости от того, какие элементы симметрии будут еще присоединяться к тройной оси симметрии, мы получим семь различных классов этой системы (см. далее). Все формы Т. системы могут обозначаться или по системе Браве, или по системе Миллера. Первый принял систему четырех осей, из которых три равных оси (оси а) лежат в горизонтальной плоскости (см. фиг. 1, a и b, первый — вид сверху, второй — в перспективе), пересекаясь под равными углами в 60°, четвертая к ним перпендикулярна (ось с) следовательно, вертикальна, причем величина ее у каждого минерала различна, больше или меньше a, напр., для кварца отношение а: с = 1: 1,099, для турмалина a: с = 1: 0,45181.
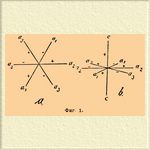
Фиг 1.
Каждая грань каждой формы обозначается символом из четырех цифр, при чем отрезки осей a обозначаются попеременно + и — (как это видно на фигуре), так что, напр., грань основной пирамиды первого рода обозначается (1011), причем порядок, в каком берутся отрезки осей, можно видеть из следующей схемы 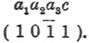 . Сумма трех первых индексов всегда равна = 0. В последнее время обозначение это почти уже не употребляется, так как оно совершенно не отвечает молекулярному строению кристаллов, и для обозначения форм Т. системы пользуются системой Мiller'а. Последний принял систему трех осей, пересекающихся под равными углами одна с другой, причем направлениями этих осей служат ребра основной Т. пирамиды (или ромбоэдра, см. фиг. 2), поэтому для каждого минерала угол между осями — α будет иной, величины же всех трех осей всегда равны. Напр., для турмалинами α = 113°51,5'. При таком обозначении основная положительная Т. пирамида (или ромбоэдр) получает символ {100}, базис {111}, призма {211} и т. д. Все верхние отрезки осей имеют знак +, все три нижние — (см. черт.). Это обозначение является вполне рациональным для всех классов Т. системы. Следует различать следующие семь классов этой системы.
. Сумма трех первых индексов всегда равна = 0. В последнее время обозначение это почти уже не употребляется, так как оно совершенно не отвечает молекулярному строению кристаллов, и для обозначения форм Т. системы пользуются системой Мiller'а. Последний принял систему трех осей, пересекающихся под равными углами одна с другой, причем направлениями этих осей служат ребра основной Т. пирамиды (или ромбоэдра, см. фиг. 2), поэтому для каждого минерала угол между осями — α будет иной, величины же всех трех осей всегда равны. Напр., для турмалинами α = 113°51,5'. При таком обозначении основная положительная Т. пирамида (или ромбоэдр) получает символ {100}, базис {111}, призма {211} и т. д. Все верхние отрезки осей имеют знак +, все три нижние — (см. черт.). Это обозначение является вполне рациональным для всех классов Т. системы. Следует различать следующие семь классов этой системы.
1) Тригонально-пирамидальный класс (гемиморфно-тетартоэдрический или огдоэдрический) — присутствует только тройная ось симметрии. Характерной формой этого класса является Т. пирамида. Представителем этого класса служит йоднокислый натрий.
2) Ромбоэдрический класс (ромбоэдрически-тетартоэдрический класс) имеет тройную ось симметрии, являющуюся в то же время шестерной осью сложной симметрии. Характерной формой служит ромбоэдр (см. фиг. 2).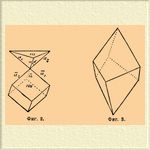
Фиг 2. Фиг 3.
Сюда принадлежат минералы: диоптаз, фенакит и т. д.
3) Тригонально-трапецоэдрический класс (трапецоэдрически-тетартоэдрический класс) — помимо одной тройной оси симметрии имеет еще три двойных оси, расположенных в плоскости, перпендикулярной к тройной оси. Характерной формой служит Т. трапецоэдр (см. фиг. 3). Сюда принадлежат минералы: киноварь, кварц и т. д., а также камфора, виноградный сахар, бензил и т. д.
4) Тригонально-бипирамидальный класс (тригонально-тетартоэдрический класс), помимо тройной оси, также плоскость симметрии, перпендикулярная к ней. Типичной формой является Т. бипирамида (см. фиг. 4). Представителей этого класса еще не найдено.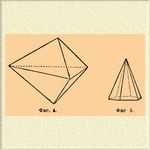
Фиг 4. Фиг 5.
5) Дитригонально-пирамидальный класс (гемиморфно-гемиэдрический) — помимо тройной оси симметрии, еще три параллельных ей плоскости симметрии. Характерная форма — дитригональная пирамида (см. фиг. 5). Сюда принадлежат минералы: турмалин, пираргирит и т. д.
6) Дитригонально-скаленоэдрический класс (ромбоэдрически-гемиэдрический) — помимо тройной оси симметрии еще три параллельных ей плоскости симметрии и три двойных оси симметрии, делящие пополам углы между плоскостями симметрии. Типичной формой является дитригональный скаленоэдр (см. фиг. 6). К этому классу принадлежат очень многие важные минералы: известковый шпат (кальцит), корунд (сапфир, рубин), железный блеск, селитра, железный шпат и т. д.
Фиг 6.
7) Дитригонально-бипирамидальный класс (тригонотипно-гемиэдрический) — помимо тройной оси симметрии — еще три параллельных ей плоскости симметрии и одна плоскость симметрии, перпендикулярная ей. Характерной формой является дитригональная бипирамида (см. фиг. 7).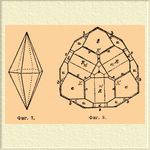
Фиг 7. Фиг 8.
Представителей этого класса еще не найдено. Понятно, что в каждом из этих классов помимо указанной характерной формы наблюдаются еще формы, представляющие частные случаи этой основной формы, напр. в 6-м классе помимо дитригонального скаленоэдра наблюдаются еще: базис, гексагональные призмы первого и второго рода, ромбоэдры, дигексагональные призмы и гексагональные бипирамиды.
Фиг. 8 изображает, напр., кристалл турмалина (пятый класс), на котором наблюдаются: Т. призма (s'), положительные Т. пирамиды (R и R') и отрицательная Т. пирамида (n'). В оптическом отношении все кристаллы Т. системы одноосны. Кристаллы классов первого и третьего вращают плоскость поляризации (см. Поляризация света). Кристаллы обладают дихроизмом (см.). Кристаллы первого, третьего и пятого классов показывают полярное распределение пироэлектричества (см. Пироэлектричество), находящееся в строгой зависимости со степенью симметрии того класса, к какому принадлежит данный минерал. Подробнее см. Groth, "Физическая кристаллография" (1897, 456—498); Е. Федоров, "Курс кристаллографии" (1897, 153—157).
В. В
| "БРОКГАУЗ И ЕФРОН" >> "Т" >> "ТР" >> "ТРИ" >> "ТРИГ" |
Статья про "Тригональная система" в словаре Брокгауза и Ефрона была прочитана 1775 раз
| Пицца в сковороде |
| Жаренный морской черенок |
TOP 15
- Волос
- Проно
- Степные животные
- Гимнастика
- Индийский океан
- Архитектура
- Сравнение, в литературе
- Манда
- Клитры
- Колесование
- Испарение
- Травоядные животные
- Оплодотворение у pacтений
- Вредные насекомые
- Электризация тел