


БНБ
"БРОКГАУЗ И ЕФРОН" (121188)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Термохимия
Определение "Термохимия" в словаре Брокгауза и Ефрона
Термохимия — отдел химии, занимающийся превращениями внутренней энергии тел в тепло при химических процессах. Почти каждая химическая реакция связана с тем или иным тепловым эффектом: химическое превращение сопровождается или выделением, или поглощением тепла. В первом случае реакция называется экзотермической, во втором — эндотермической. Тепловой эффект реакций является мерилом изменения внутренней энергии тел, участвующих в химическом превращении. Взаимные превращения различных видов энергии составляют предмет термодинамики, установившей законы таких превращений; поэтому в основе Т., занимающейся одним из видов таких превращений, лежат законы термодинамики, приложение которых к химическим явлениям и составляет содержание Т. Соответственно этому, дальнейшее изложение разделено на три части: очерк развития Т., приложения I закона и приложения II закона термодинамики.
История термохимии. До Лавуазье тепловой эффект химических реакций объяснялся выделением или поглощением флогистона (см. Флогистон). Лавуазье, показавшему отличие между материей весомой и невесомой, т. е. между тем, что называется теперь веществом, и различными видами энергии, принадлежат и первые термохимические исследования (теплоты горения и теплоты, выделяемой животными), произведенные им совместно с Лапласом с помощью ледяного калориметра. Из теоретических воззрений Лавуазье и Лапласа имеет значение положение, принимавшееся ими за аксиому, что при разложении химического соединения на его составные части затрачивается столько же тепла, сколько его выделяется при образовании этого соединения. Другие исследователи в области Т., работавшие в конце XVIII и начале XIX стол., как то: Крауфорд, Румфорд, Дэви, Дальтон, Дюлонг, Депре, не дали научных оснований для Т. Истинным основателем Т. явился Гесс в своих работах, напечатанных в изданиях Петербургской акад. наук в 1839—1844 гг. Закон постоянства сумм тепла, установленный им в 1840 г. и гласящий, что выделение тепла, сопровождающее химическую реакцию, всегда одно и то же независимо от того, протекает ли реакция сразу, или она разбивается на ряд промежуточных реакций, является основным законом Т. Не останавливаясь на других выводах и обобщениях Гесса, опровергнутых позднейшими исследователями, замечу, что он указал на явление термонейтральности (см. дальше), хотя и дал ему неверное объяснение. Андрюс и Грэм в современных Гессу работах дали кое-какой фактический материал, не давши ничего теоретическому развитию Т.; еще меньшее значение имели работы Ходнева, Абриа, Грасси, Вуда, числовые данные которых крайне неточны, а подчас и прямо неверны. Новый толчок в развитии Т. дали Фавр и Зильберман, 1852—53. Новые методы калориметрических определений (см. Калориметрия) и множество разнообразных химических реакций, тепловые эффекты которых были изучены названными исследователями, обеспечили за ними выдающееся место в среде термохимиков. Менее удачны были их теоретические объяснения наблюденных фактов. Правда, они дали правильное объяснение явлению термонейтральности, зато в других случаях они не могли отрешиться от господствовавших тогда неверных взглядов. Так, общепринято было мнение, что всякая реакция соединения сопровождается выделением тепла, и обратно, — при разложении тепло поглощается. Фавр и Зильберман, первые нашедшие соединения, разлагающиеся с выделением тепла, именно сернистый углерод, закись азота и перекись водорода, старались объяснить такое явление аллотропическим изменением элементов перед образованием соединения и при разложении его, считая, что сама реакция соединения все же идет с выделением тепла. Фавру же и Зильберману принадлежит открытие различных теплот горения для различных аллотропических состояний углерода и серы. Таково было положение Т. до появления работ Томсена, который был первый термохимик, применивший механическую теорию тепла к химическим явлениям. В своей статье, появившейся в 1853 г. ("Grandz ü ge eines thermochemischen Systems", "Poggendorff's Annalen", т. 88), он, исходя из первого закона термодинамики, закона сохранения энергии, следующим образом формулирует основные принципы Т. При этом надо заметить, что терминология Томсена отличается от употребляемой ныне: он говорить "сила" вместо работа или энергия. Интенсивность химической силы (запас химической энергии) одного и того же тела при неизменной температуре есть величина постоянная. При превращении тела в другое, отличающееся от первого термохимически, т. е. обладающее другим запасом химической энергии, развивается некоторая работа. Эта работа может быть измерена: она есть не что иное, как выделяющееся при реакции тепло. Поэтому все количество тепла, образующееся при химической реакции, есть мера развитой процессом химической силы (работы). Алгебраическую сумму количеств тепла выделенных и поглощенных при реакции, причем выделенное тепло принимают за величину положительную, поглощенное — за отрицательную, Томсен назвал тепловым эффектом (Wärmetö nung) реакции. Представляя себе, что запас химической энергии вещества может быть использован целиком, полученное таким образом количество тепла, измеренное в единицах количества тепла (калориях) и отнесенное к эквивалентному весу вещества, Томсен назвал термохимическим эквивалентом. Величина теплового эффекта образования химического соединения есть разница между суммой термохимических эквивалентов веществ, образующих соединение, и термохимическим эквивалентом образовавшегося соединения. Из этого принципа видно, что тепловой эффект реакции не зависит от того, тем или иным путем идет реакция, лишь бы исходные вещества и продукты реакции были одни и те же; а это и есть сущность закона Гесса. Таким образом, Томсен выводит закон Гесса из первого закона термодинамики. В 1854 г. Томсен высказывает следующий принцип: каждый простой или сложный чисто химический процесс сопровождается выделением тепла. Этот принцип гипотетического характера является первой попыткой предсказания при помощи теплового эффекта направления хода химической реакции. Но уже сам Томсен, применяя этот принцип, натолкнулся на противоречащие ему факты. С 1865 г. стали появляться статьи Бертело, в которых он, независимо, по-видимому, от Томсена, выводит основные законы Т. Окончательная форма, в которую вылилось применение первого закона термодинамики к химическим явлениям, выражена им в следующих двух принципах. I. Принцип молекулярных работ: количество тепла, выделенное какой-нибудь реакцией, есть мера совокупности химических и физических работ, совершенных в этой реакции. II. Принцип термической эквивалентности химических превращений, или иначе — принцип начального и конечного состояний: если система простых или сложных тел, взятая в определенных условиях, претерпевает физические или химические превращения, способные привести ее к новому состоянию, не сопровождаясь при этом никаким внешним по отношению к системе механическим эффектом, количество выделенного или поглощенного этими превращениями тепла зависит только от начального и конечного состояний системы; количество тепла одно и то же, каковы бы ни были природа и порядок промежуточных состояний. В своих исследованиях Бертело подробно разрабатывает влияние на тепловой эффект превращений различных факторов, именно влияние агрегатного состояния веществ, участвующих в реакции, влияние внешней механической работы, производимой системой во время превращения и влияние температуры. Последнее, т. е. влияние температуры на тепловой эффект химических реакций, впервые было указано Кирхгоффом уже в 1858 г. На этом заканчивается теоретическое развитие применения закона сохранения энергии в Т. — Томсену и Бертело принадлежит также и заслуга разработки экспериментальной стороны Т. После отдельных экспериментальных исследований, произведенных в пятидесятых годах, Томсен начинает в 1869 г. обширнейшие, по строго систематическому плану, работы, результаты которых собраны в четырех томах, изданных в 1882—1886 гг. ("Thermochemische Untersuchungen"). В 1875 г. Бертело начинает свои исследования и ведет их без перерыва и по настоящее время; числовой материал работ Бертело и его многочисленных учеников публикуется в "Annales de chimie et de physique" и собирается в "Essai de m écanique chimique fondée sur la therm ochimie", 1879, и в "Thermochimie. Donn ées et lois numé riques", 1897 г. Эти исследователи совершенствуют известные и разрабатывают новые калориметрические методы и методы термохимического исследования всевозможных реакций. Взаимная проверка исследователей дает высокую степень точности огромной массе собранного ими материала. При этом надо заметить, что данные Томсена, полученные все при 18°, имеют преимущество в смысле большой сравнимости перед данными Бертело, производившего свои определения в пределах температур между 10° и 20°.
Изучение теплового эффекта химических превращений поставило на очередь вопрос о том, какая из возможных для взятых тел реакций будет иметь место при данных условиях. Выше уже было указано, что Томсен в 1854г. пытался это сделать, говоря, что каждый простой или сложный чисто химический процесс сопровождается выделением тепла. На основании этого положения только экзотермическая реакция идет непосредственно, сама по себе, реакции же эндотермические могут быть воспроизведены лишь окольным путем. Этим же вопросом занялся и Бертело. Подходя к решению его постепенно в первых своих исследованиях по Т., он в 1873 г. окончательно сформулировал свой третий принцип Т., принцип максимальной работы: всякое химическое превращение, совершающееся без участия посторонней энергии, ведет к образованию тела или системы тел, выделяющих наибольшее количество тепла. Этот принцип Бертело кладет в основу химической механики, посвящая, между прочим, его применению второй том своего "Essai de m écanique chimique". Соображения, посредством которых Бертело вывел свой принцип максимальной работы, основаны на законе сохранения энергии. Это можно заключить из следующих его слов: "необходимость этого принципа видна из того, что система, выделившая наибольшее возможное количество тепла, не обладает сама по себе запасом энергии, необходимой для нового превращения. Всякое новое превращение требует затраты работы, не могущей быть произведенной без участия посторонней энергии. Наоборот, система, способная еще выделить тепло при новом превращении, заключает в себе энергию, необходимую для этого превращения безо всякой посторонней помощи". Согласуясь во многих случаях с фактами, принцип максимальной работы оказался неприменимым к целому ряду данных опыта. Уже Томсену пришлось встретиться с такими противоречиями: так, он нашел, что хлористый водород не реагирует с серебром и ртутью, хотя эти реакции должны выделять значительное количество тепла. В других случаях реакции идут с поглощением тепла. Дальнейшие исследования разных ученых указывали все большее и большее число случаев, когда принцип максимальной работы оказывался неприменимым. Все такие противоречия Бертело старался объяснить участием посторонней энергии: света, электричества в виде гальванического тока, тихого разряда или искры, энергии дезагрегации, развиваемой растворением. Работы Сент-Клэр-Девилля и его учеников над диссоциацией при высоких температурах, показавшие, что в этих условиях разлагаются прочнейшие химические соединения, образующиеся с выделением громадных количеств тепла, как, напр., вода и хлористый водород, заставили Бертело причислить к числу внешних энергий и тепло. Этим Бертело отнял у своего принципа его значение: если всякое химическое превращение, совершающееся без участия посторонней энергии, выделяет тепло, то, принимая во внимание, что участие тепла как посторонней энергии выражается поглощением тепла, — мы получим следующее выражение для частного случая применения принципа максимальной работы: всякое химическое превращение, идущее без поглощения тепла, выделяет тепло. Основная ошибка Бертело была та, что он положил в основание своего принципа максимальной работы первый закон термодинамики, закон сохранения энергии. На самом деле этот закон совершенно не касается вопроса о направлении протекающих в природе процессов; вопрос этот составляет содержание второго закона термодинамики. Так, в случае двух тел различной температуры, с помощью теплопроводности обменивающихся теплом, закон сохранения энергии требует только, чтобы количество тепла, отданное одним телом, было равно количеству тепла, принятому вторым; и только II закон указывает, что отдает тепло тело с высшей температурой, а принимает — тело с более низкой температурой. Направление процесса обусловливается изменениями не энергии, а энтропии системы. В то время, когда Бертело разрабатывал свой неверный принцип, появилась в анналах Либиха за 1873 г. статья Горстмана о теории диссоциации. В этой статье в первый раз II закон термодинамики был приложен к химическим явлениям. Выводы Горстмана следующие: при диссоциации равновесие наступает тогда, когда энтропия приняла наибольшую из возможных при данных превращениях величину. Вообще, говорит он, возможно только такое химическое превращение, при котором энтропия увеличивается. Эти положения не были изменены дальнейшими исследованиями. Разработка их повела к более детальному приложению II закона термодинамики к химическим явлениям, выяснению влияния различных факторов на направление химического превращения и к изучению химических равновесий, чем были положены основы современной химической механики. Классическими в этой области явились исследования Гиббса, "On the equilibrium of heterogenous substances" в "Tran s actions of Connecticut Academy" (т. III, 1875) и Гельмгольца, "Zur Thermodynamik chemischer Vorg änge " в "Sitzungsberichte der Berliner Akademie" (1882). Необходимо также указать имена Мутье, Робэна, Вант-Гоффа, Лешателье и Дюгема, внесших свою долю в разработку отдельных сюда относящихся вопросов.
Приложения I закона термодинамики. В предыдущем были указаны принципы, основанные на законе сохранения энергии и применявшиеся в Т. Здесь мы изложим их так, как они применяются в настоящее время — в крайне простом и сжатом виде. Закон сохранения энергии для случая превращения внутренней энергии в тепло и механическую работу выражается уравнением: dU = dQ + dr, где: dU — изменение внутренней энергии системы, dQ — выделенное или поглощенное системой тепло, a dr — внешняя, механическая работа, произведенная системой. Во всех случаях, когда в реакции не участвуют газы, внешняя работа dr может быть опущена благодаря ничтожной величине ее. Уравнение превращается в dU = dQ и после интегрирования получается: U1 — U2 = Q, где U1 — внутренняя энергия начального, а U2 — внутренняя энергия конечного состояния системы, Q — тепловой эффект превращения. В Т. принято считать величину Q положительной, когда превращение совершается с выделением тепла. В более наглядной форме: U1 = U2 + Q выражает, что внутренняя энергия тел до реакции равна внутренней энергии тел после реакции плюс выделенное системой тепло. Это есть простейшее выражение закона Гесса и первых двух принципов Бертело. Определение величины Q производится калориметрически, что описано подробно в статье Калориметрия (см.). Единицы тепла приняты в Т. следующие: 1) малая калория — количество тепла, требуемое для нагрева 1 грамма воды от 0° до 1°, она обозначается cal.; 2) большая калория, введенная Бертело и равная 1000 малым, обозначается Cal. В Германии по предложению Оствальда употребляются 3) новая калория Шюллера и Варта, равная количеству тепла, нужному для нагрева 1 грамма воды от 0° до 100°; она равна 100 малым калориям, соответствующим количеству тепла, необходимому для нагрева 1 грамма воды на 1° при температуре, близкой к 18°, т. е. температуре громадного большинства термохимических определений. Новая, или, как ее часто называют, средняя калория обозначается К; 4) наконец, в 1899 г. Оствальд в своем "Grundriss der allgemeinen Chemie" вводит калорию, основанную на абсолютной системе С. G. S. единиц, именно "джоуль", обозначаемый j; j = 0,2391 cal. = 10 7 эргов. 1 cal. = 4,183 j. Более удобна для практического применения единица, в 1000 раз большая: J = 239,1 cal. = 10 10 эргов. Все термохимические определения относятся к грамм-молекулярным количествам веществ. Для выражения результатов термохимических определений предложены особые приемы. Наиболее употребительны томсеновский и оствальдовский. Томсен ставит химические формулы реагирующих веществ рядом, разделяя их запятыми и заключая все в скобки; знак равенства соединяет это выражение с тепловым эффектом реакции. Так (Н,Сl) = 22001 cal. — обозначает, что соединение 1 грамма водорода с 35,46 граммами хлора выделяет 22001 cal. Оствальдовское обозначение не столь сокращенно, зато представляет больше систематичности и удобства для расчетов. Он употребляет обыкновенно химическое равенство, прибавляя ко второй части тепловой эффект реакции; при этом химические формулы обозначают не только атомные количества, но и запас внутренней энергии соответствующих тел. Для разных агрегатных состояний употребляется различный шрифт: обыкновенный для жидкого, жирный для твердого и курсив для газообразного. Иногда вместо разных шрифтов употребляют разные скобки: формула жидкого вещества заключается в скобки — (), твердого — [], газообразного — {}. В случае, когда тела берутся при другой температуре, чем обычная в 18°, подле формулы в скобках ставится температура. Так, (Н 2O)(0) = [Н 2O](0) + 14,4 К обозначает, что 18 грамм воды, превращаясь при 0° в лед, выделяют 14,4 К. С оствальдовским выражением можно обращаться, как с алгебраическим уравнением, перенося члены из одной части в другую с переменой знака, складывая или вычитая почленно одни уравнения с другими. При всяких обозначениях в реакциях, идущих в растворах при разбавлениях, когда дальнейшая прибавка растворителя не вызывает заметного теплового эффекта, принято растворитель обозначать особым выражением: aq. для воды, alc. для алкоголя и т. д. Так, образование хлористого калия из едкого кали и хлористого водорода, причем все вещества взяты в растворах, пишется — по Томсену: (KOHaq, HClaq) = 13700 cal.; по Оствальду: KOHaq + HClaq = KClaq + Н 2 O + 137 К.
Влияние температуры на тепловой эффект выражается следующим образом: тепловой эффект реакции Qt2 при какой-нибудь температуре t2 равен тепловому эффекту Qt1, определенному при другой температуре t1, увеличенному на произведение разницы сумм молекулярных теплоемкостей веществ до и после реакции, помноженной на разницу температур. Если обозначить через с' теплоемкость, а через m' молекулярный вес каждого вещества, вступающего в реакцию, через с и m те же величины для отдельных продуктов реакции, вышеуказанное положение примет следующий вид:
Qt2 = Qt1 + (Σ m'c' — Σ mc)(t2 — t1).
В случае, если величины теплоемкостей меняются с температурой, то необходимо или брать средние теплоемкости между температурами t1 и t2, или, выражая теплоемкость функцией температуры, заменить каждый член mc(t2 — t1) соответствующим интегралом
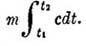
Влияние внешней работы на тепловой эффект. Выше было указано, что, если в реакции не участвуют газообразные вещества, внешняя работа может не приниматься в расчет ввиду ее ничтожной величины. Если же при реакции выделяются или поглощаются газы, то необходимо ввести соответствующую поправку. В обычных условиях, когда реакция ведется при постоянном атмосферном давлении, зависимость между истинным тепловым эффектом реакции Q и наблюденным при постоянном давлении Qp выражается уравнением:
Q = Qp — 2(n' — n)T саl., где T — абсолютная температура реакции; n' и n — число грамм-молекул газа до и после реакции; 2 — константа R уравнения состояния газов pv = RT. Величина внешней работы не зависит от давления, если только во время реакции давление остается постоянным. В тех случаях, когда реакция ведется при постоянном объеме, как это имеет место в калориметрической бомбе Бертело, внешняя работа газа равна нулю и наблюдаемый тепловой эффект равен истинному.
Определения теплового эффекта косвенным путем. Очень часто по тем или иным причинам тепловой эффект реакции не может быть определен непосредственно. В таких случаях его вычисляют из тепловых эффектов, непосредственно определенных для нескольких реакций, подобранных таким образом, чтобы, если бы они были произведены последовательно, то в результате получилось бы то превращение веществ, тепловой эффект которого требуется определить. Для пояснения приведем пример. Теплота образования окиси углерода из элементов не может быть определена непосредственно; известны теплоты горения углерода в углекислоту и окиси углерода в углекислоту. Если сжечь сперва уголь в углекислоту, а затем разложить полученную углекислоту на СО и кислород, то, очевидно, результат этих двух реакций выразится: С + О = СО. Тепловой эффект последней реакции получим, вычтя из теплоты горения углерода в углекислоту теплоту горения окиси углерода в углекислоту, так как последняя имеет ту же величину, но с обратным знаком, как теплота разложения СО 2 на кислород и СО. С помощью Оствальдовского обозначения такие расчеты производятся крайне просто. Написав, что при постоянном объеме:
С + 2O = СО 2 + 97000 cal.
СО + О = СО 2 + 68000 cal.
и вычтя почленно второе уравнение из первого, получим искомый результат: С + О = СО + 29000 cal. Для вычислений тепловых эффектов всевозможных реакций с помощью имеющихся уже термохимических данных пользуются расчетом по теплотам образования сложных веществ из элементов. Расчет производится на основании правила: тепловой эффект реакции равен разности суммы теплот образования продуктов реакции и суммы теплот образования веществ до реакции. Так, подписывая под веществами их теплоты образования, находим для реакции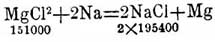
тепловой эффект равным 239800 cal. Для целей таких расчетов в справочных книгах термохимические данные приводятся в виде теплот образования из элементов, причем для каждого вещества даются числа: для твердого, жидкого, газообразного и растворенного (в воде) состояний.
Теплоты растворения и разбавления. Теплота растворения определенного количества (грамм-молекулы) вещества зависит от количества взятого для растворения растворителя, иначе говоря, от концентрации образующегося раствора. При постепенном увеличении количества растворителя теплота растворения достигает некоторой величины, не изменяющейся при дальнейшем прибавлении растворителя. Эта предельная величина называется теплотой растворения при бесконечном разведении, иногда же, что хуже, просто теплотой растворения. Достигается этот предел для разных веществ при различных количествах растворителя; обыкновенно, чем больше величина теплоты растворения, тем дольше лежит предел. Так, для аммиака NH 3, выделяющего при бесконечном разведении 88 K., предел уже достигнут, когда образовался раствор состава NH 3 ·50Н 2 O, для хлористого водорода НСl, выделяющего 174 K., — предел лежит при образовании раствора HCl·200H 2 O, для серной кислоты H 2SO4 при выделении 892 K. предел еще не достигнут при растворе Н 2 SО 4 ·800Н 2 O. В последнее время в химической механике стала употребляться иногда другая величина, теплота растворения до насыщения, соответствующая теплоте растворения вещества в таком количестве растворителя, чтобы образовался насыщенный раствор. Теплота разбавления раствора от большей концентрации к меньшей есть разность теплот растворения при меньшей и при большой концентрациях. Теплота концентрирования раствора есть величина, обратная теплоте разбавления, наблюдаемая при растворении в данном растворе новых количеств растворенного тела, что ведет к увеличению концентрации раствора.
Теплоты растворения газов. При растворении в жидкостях газы распадаются на две резко отличающиеся группы. Газы, следующие закону Генри, т. е. такие, растворимость которых увеличивается пропорционально давлению, дают при растворении столь незначительный тепловой эффект, что он не мог быть еще до сих пор определен. Газы, не следующие закону Генри, имеют значительные положительные величины теплот растворения, превышающие теплоты сжижения их. В следующей таблице приведены теплоты растворения в воде при бесконечном разведении Q некоторых газов и паров при температуре 15—20° и их теплоте сжижения q.
| QK. | qK. | QK. | qK. | QK. | qK. | |||
| Cl2 | 30 | — | HNO3 | 144 | 73 | СН 3 —СО 2H | 76 | 73 |
| Br2 | 83 | 72 | SO2 | 77 | 62 | СН 3 —СОН | 89 | 60 |
| НСl | 174 | — | Сl 2O | 94 | — | СН 3 —СН 2 OН | 124 | 98 |
| HBr | 200 | — | СО 2 | 58 | 61 | (C2H5)2O | 126 | 67 |
| HJ | 194 | — | COCl2 | 580 | — | CH3—CO2(C2H5) | 140 | 109 |
| H2S | 47 | — | COS | 68 | — | (C2O4)(C2H5)2 | 337 | 106 |
| NH3 | 88 | 44 | HCN | 61 | 57 | CHCl3 | 95 | 73 |
| NO2 | 78 | 43 | HCO2H | 57 | 56 | ССl 3 —СОН | 199 | 80 |
Поглощение газов твердыми телами также сопровождается положительным тепловым эффектом. В случае пористых, обладающих большой поверхностью твердых тел, при значительном объеме поглощенного газа выделяются значительные количества тепла, в большинстве случаев превосходящие теплоты сжижения. Так, 100 г платиновой черни, поглощая 0,1 г водорода, выделяют 414 К. При поглощении углем более плотные сорта угля, поглощая меньше газа, чем менее плотные сорта, выделяют на одно и то же количество газа большие количества тепла. Первые порции поглощенных газов выделяют больше тепла, чем последние.
| Газы | Выделенное тепло | ||
| при различных условиях | до насыщения | Теплота сжижения | |
| NH3 | 49—88 К. | 84 К. | 44 К. |
| HCl | 92—102 | 100 | — |
| HBr | — | 155 | — |
| HJ | — | 220 | — |
| SO2 | 10—110 | 108 | 56 |
| СО 2 | 66—78 | 70 | 61 |
| N2O | 72—76 | 74 | 44 |
Теплоты растворения жидкостей друг в друге имеют обыкновенно положительные величины. В случае растворения в воде органических веществ тепловой эффект бывает незначителен; сильные неорганические кислоты, наоборот, дают гораздо большие величины.
В следующей таблице приведены некоторые относящиеся сюда данные для теплот растворения при бесконечном разведении.
| QK | |
| CH3—OH | 20 |
| C2H5—OH | 25 |
| C3H7 —OH н. | 31 |
| C3H7 —OH изо. | 35 |
| C4 Н 9 —ОН изо. | 29 |
| С 5H11 —ОН изо. | 28 |
| C3H5(OH)3 | 15 |
| (CH3)2CO | 25 |
| СН 2 =СН—СН 2 —ОН | 21 |
| C2H5—COH | 40 |
| CH3—COH | 36 |
| ССl 3 —СОН | 119 |
| (C2H5)2 Ο | 59 |
| ΝΟ 3(C2 Η 5) | 10 |
| СН 3 —СО 2(C2 Н 5) | 31 |
| (С 2O4)(C2H5)2 | 31 |
| НСО 2H | 1 |
| CH3—CO2H | 4 |
| C3H7—CO2H | 10 |
| С 4H9 —СО 2H | 8 |
| HCN | 4 |
| HNO3 | 72 |
| H2SO4 | 89 |
Для азотной и серной кислот Томсен дал эмпирические формулы для теплот растворения
(Н 2SO4, nН 2O) = [n/(n + 1,798)]178,6 К.; формула годна для n от 0 до 20.
(HNO3, nН 2O) = [n/(n + 1,737)]89,74 К.;
формула годна для n от 0 до 5.
Теплоты разбавления неорганических сильных кислот уменьшаются по мере увеличения содержания воды в разбавляемом растворе. Для азотной кислоты теплота разбавления, будучи сперва положительной, уменьшаясь, меняет знак и становится отрицательной, т. е. разведение слабых растворов HNO 3 идет с поглощением тепла. Для теплот разбавления растворов галоидоводородных кислот имеются эмпирические формулы:
(НСlnН 2O, aq) = 119,8/n К.
(НВrnН 2O, aq) = [(120,6/n) — 2] К. до n = 40;
при n > 40, Q = 120,6/n К.
(HJnН 2O, aq) = [(1174/n) — 5] К. до п = 20;
при n > 20, Q = 19,57/n К.
Крайне своеобразно изменение теплот растворения этилового алкоголя в воде с повышением температуры. Теплоты растворения грамм-молекулы C 2H5 OH в таких количествах воды, чтобы образовался раствор с содержанием р % алкоголя, следующие:
| р %. | Q.K. | p %. | Q.K |
| 90 | 0,787 | 30 | 14,71 |
| 80 | 1,435 | 20 | 20,22 |
| 60 | 4,18 | 10 | 24,55 |
| 40 | 10,32 |
При повышении температуры теплоты растворения понижаются пропорционально их величинам так, что при температурах кипения спирто-водных растворов теплоты образования этих последних из жидких воды и алкоголя становятся равными нулю.
Теплота растворения твердых тел. Наиболее важным фактором, влияющим здесь на величину теплового эффекта, является способность растворенного вещества образовать соединения с растворителем, в случае растворения в воде — способность образовать кристаллогидраты. Вещества, не образующие кристаллогидратов, стойких при обыкновенной температуре, при которой производится определение теплоты их растворения, растворяясь в воде, почти без исключения поглощают тепло. Как примеры можно привести:
| (KCl, aq) | = —44,4 К. |
| (NaCl, aq) | = —11,8 К. |
| (KNO3, aq) | = —85,2 К. |
| (K2SO4, aq) | = —31 К. |
| [(NH4)2SO4, aq] | = —12 К. |
| (KClO3, aq) | = —100 К. |
| (NaClO3, aq) | = —56 К. |
| (KClO4, aq) | = —121 К. |
| (KMnO4, aq) | = —104 К. |
Сюда же относится целый ряд органических соединений.
Соединения, образующие кристаллогидраты, будучи в безводном состоянии, в большинстве случаев выделяют тепло. Растворение соответствующего безводному веществу кристаллогидрата сопровождается всегда меньшим выделением тепла, очень часто даже — поглощением. Теплота растворения для веществ, способных образовать несколько кристаллогидратов, тем меньше, чем больше содержание воды в растворяемом кристаллогидрате. Ряд нижеследующих примеров наглядно поясняет эти положения:
| (KHO, aq) | = 124,6 К. | |||||||
| (KНО·H 2 O, аq) | = 36 К. | |||||||
| (NaНО·2H 2 O, аq) | = —0,3 К. | |||||||
| (NaHO, aq) | = 97,8 К. | |||||||
| (NaHO·H2O, aq) | = 65 К. | |||||||
| (Ba(OH)2, aq) | = 102 К. | |||||||
| (Ва(OH) 2·9H2 O, аq) | = —142 К. | |||||||
| (Sr(ОН) 2, aq) | = 96 К. | |||||||
| (Sr(ОН) 2·9H2O, aq) | = 150 К. | |||||||
| (NaBr, aq) | = —2 К. | |||||||
| (NaBr·2H2O, aq) | = —47 К. | |||||||
| (CaCl2, aq) | = 174,1 К. | |||||||
Статья про "Термохимия" в словаре Брокгауза и Ефрона была прочитана 5521 раз |
TOP 15
|
|||||||