


БНБ
"БРОКГАУЗ И ЕФРОН" (121188)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Теория вероятностей
Определение "Теория вероятностей" в словаре Брокгауза и Ефрона
Теория вероятностей — есть часть математики, изучающая зависимости между вероятностями (см. Вероятность и Статистика) различных событий. Перечислим важнейшие теоремы, относящиеся к этой науке. Вероятность появления одного из нескольких несовместных событий равняется сумме вероятностей этих событий. Приведем пример. Вероятность вынуть туза из полной колоды карт равна 4/52, или 1/13, так как всего карт 52 и из них 4 туза; вероятность вынуть короля тоже равна 1/13. Вероятность вынуть туза или короля будет 1/13+1/13 = 2/13. Рассматриваемые события несовместны, так как появление одного из событий исключает появление другого. Вероятность вынуть туза или трефовую карту не равна 1/13 + 1/4, так как вынутый туз мог бы оказаться трефовой масти. В этом случае события нельзя назвать несовместными и потому нельзя прилагать высказанной теоремы, вероятность появления событий Е и F равна вероятности Е, умноженной на вероятность F, вычисленную в том предположении, что Е случилось. Например, вероятность вынуть два туза из полной колоды карт равна (4/52)∙(3/51), так как после появления туза в колоде останется 51 карта и в том числе 3 туза. Если же вынимать карты последовательно и вынутую карту возвратить в колоду, то вероятность вынуть 2 туза равна (4/52) 2. Предположим, что при повторении испытаний вероятность появиться событию Е постоянно остается равною р. В таком случае вероятность того, что при п испытаниях событие Е появится т раз, будет
1.2.3...n
1.2.3...(n — m)k(1 — p)n—m , где k = pm.
Если п и т очень велики, то Лаплас доказал, что интеграл 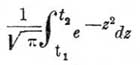 есть приближенное выражение вероятности того, что т заключается между
есть приближенное выражение вероятности того, что т заключается между 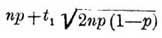 и
и 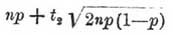 . Отсюда легко выводится следующая теорема Якова Бернулли. С вероятностью, сколь угодно близкою к достоверности, можно утверждать, что при достаточно большом п численное значениe разности (m/n — р) сколь угодно мало. Предположим, что вероятность события Е меняется при каждом испытании и что при n испытаниях эта вероятность принимала значения p1, p2,... рп. Если т обозначает число появлений события Е при п испытаниях, то при достаточно большом п имеет место теорема Пуассона. С вероятностью, сколь угодно близкою к достоверности, можно утверждать, что численное значение разности m/n = (p1+p2+...+pn)/n сколь угодно мало.
. Отсюда легко выводится следующая теорема Якова Бернулли. С вероятностью, сколь угодно близкою к достоверности, можно утверждать, что при достаточно большом п численное значениe разности (m/n — р) сколь угодно мало. Предположим, что вероятность события Е меняется при каждом испытании и что при n испытаниях эта вероятность принимала значения p1, p2,... рп. Если т обозначает число появлений события Е при п испытаниях, то при достаточно большом п имеет место теорема Пуассона. С вероятностью, сколь угодно близкою к достоверности, можно утверждать, что численное значение разности m/n = (p1+p2+...+pn)/n сколь угодно мало.
Если величина х может принимать значения x1, x2,...x п , вероятности которых суть p1, p2,... рп, то число x1p1+x2p2+...+xnpn называется математическим ожиданием величины х.
Если а, b, с,...k математические ожидания независимых величин x, y, z,... и, а а 1, b1, c1,...k1 математические ожидания квадратов этих величин, то с вероятностью большей чем 1 —1/t2 можно утверждать, что x+y+ z+...+u принимает значение, лежащее между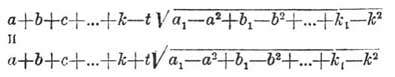
В этом состоит теорема Чебышева.
В случае большого числа величин х, у, z,...u Лаплас доказал, что интеграл 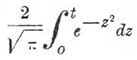 есть приближенное выражение вероятности того, что x+y+z+...+u принимает значение, лежащее между
есть приближенное выражение вероятности того, что x+y+z+...+u принимает значение, лежащее между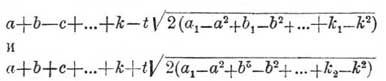
Предположим, что а, b, с,...k больше некоторого положительного числа А, а каждое из чисел a1, b1, с 1...k1 не превышает числа B. Если n, число величин х, y, z,... u, может быть сколько угодно велико, то с вероятностью, сколь угодно близкою к достоверности, можно утверждать, что сумма х+у +z+...+u превзойдет любое данное число. На основании этой теоремы определяется выгодность или убыточность предприятия. Если математическое ожидание прибыли от какого-нибудь предприятия число положительное, то такое предприятие выгодное. Хотя и возможны убытки, но с вероятностью, сколь угодно близкой к достоверности, прибыль будет сколь угодно велика, если продолжать участие в предприятии.
Литература. В. Я. Буняковский, "Основания математической теории вероятностей" (СПб., 1846); В. П. Ермаков, "Teopия вероятностей" (Киев, 1879); П. А Некрасов, "Teopия вероятностей" (М., 1896); Н. А. Забудский, "Теория вероятностей и применение ее к стрельбе и пристрелке" (СПб., 1898); М. А. Тихомандрицкий, "Курс теории вероятностей" (Харьков, 1898); А. А. Марков, "Исчисление вероятностей" (СПб. 1900); Laplace, "Th éorie analytique des probabilité s" (П., 1820); Poisson, "Recherches sur la probabilit é des jugements en matière criminelle et en matiè re civile" (П., 1837); Poisson, "Lehrbuch der Wahrscheinlichkeitsrechnung und deren wichtigsten Anwendungen" (нем. перев. Schnuse, Брауншвейг, 1841); Lacroix, "Trait é élémentaire du calcul des probabilité s" (4-е изд. Пар., 1864); Todhunter, "A history of the mathematical theory of probability..." (Кембридж и Лонд., 1865); Lauren t, "Traité du calcul des probabilité s" (П., 1873); A. Meyer, "Calcul des probabilit é s" (Льеж, 1874); Liagre, "Calcul des probabilit é s" (Брюссель, 1879); Hagen, "Grundz ü ge der Wahrscheinlichkeitsrechnung" (Б., 1882); J. Bertrand, "Calcul des probabilit és" (П., 1889); Bobek, "Lehrbuch der Wahrscheinlichkeitsrechnung" (Штутгарт, 1891); P. Poincare, "Calcul des probabilit é s" (П., 1896); Jakob Bernoulli, "Ars conjectandi" (1713; нем. перев., Haussner, Лпц., 1899); Ostwald's "Klassiker der exacten Wissenschaften" №№ 107 и 108.
Д. С.
| "БРОКГАУЗ И ЕФРОН" >> "Т" >> "ТЕ" >> "ТЕО" |
Статья про "Теория вероятностей" в словаре Брокгауза и Ефрона была прочитана 1327 раз
| Коптим скумбрию в коробке |
| Каракатица на гриле |
TOP 15
- Волос
- Проно
- Степные животные
- Гимнастика
- Индийский океан
- Архитектура
- Сравнение, в литературе
- Манда
- Клитры
- Колесование
- Испарение
- Травоядные животные
- Оплодотворение у pacтений
- Вредные насекомые
- Электризация тел