


БНБ
"БРОКГАУЗ И ЕФРОН" (121188)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Средние величины в метеорологии
Определение "Средние величины в метеорологии" в словаре Брокгауза и Ефрона
Средние величины в метеорологии — Представим себе, что изменения некоторого метеорологического элемента наблюдаются непрерывно, или, по крайней мере, настолько часто, что по полученным числам можно проследить их малейшие колебания за данный промежуток времени.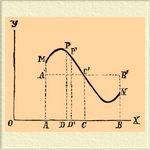
Отложим в прямолинейной, прямоугольной системе координат по оси абсцисс OX промежутки времени, по оси ординат OY — наблюденные нами величины элемента. За промежуток времени, охваченный нашими наблюдениями, наблюдаемый элемент может быть изображен тогда кривой MC'N, проведенной через нанесенные нами точки. Через некоторую точку С' проведем прямую A'С'В', параллельную оси OX; если точка С' выбрана таким образом, чтобы площадь прямоугольника AA'B'B была точно равна площади AMNB, ограниченной кривой MN, ординатами AM и BN и отрезком AB оси ОХ, то ординату СС' и называют средней из всех ординат от AM до BN. При этом условии площади отрезков МА'C и NB'C' равны. Таким образом, согласно этому определению, С. для некоторого рода наблюденных величин есть, строго говоря, ордината прямоугольника, равновеликого площади, которая ограниченна кривой, изображающей непрерывный ход изменений наблюдаемого элемента, осью абсцисс и двумя ординатами, соответствующими началу и концу избранного для наблюдений промежутка времени; при этом сумма положительных отклонений элемента от средней всегда строго равна сумме отрицательных его отклонений. Из сказанного видно, что среднюю величину для данного элемента найти легко, если мы имеем его непрерывный ход за избранный промежуток времени; для этого стоит только измерить планиметром площадь AMNB и разделить ее на длину отрезка AB. Но то же может быть достигнуто и более простыми способами. Разбивая площадь AMNB ординатами на весьма малые отрезки, например DPP'D', и полагая, что от P до P' кривая может считаться за весьма малый отрезок прямой, легко определить площадь DPPD' как площадь трапеции. Суммируя все такие весьма малые площади, найдем величину площади AMNB. Эта последняя величина определена будет тем точнее, чем меньше промежутки РР' и, следовательно, чем чаще взяты значения ординат DP, D'P'. Можно для измерения площади AMNB применить и другие методы, но метод трапеций наиболее прост и дает даже при сравнительно больших промежутках настолько удовлетворительные результаты, что в метеорологии исключительно им и пользуются для получения С. Применяя ее, например, к выводу суточной средней для различных метеорологических элементов, не трудно убедиться, что уже при 24 наблюдениях в сутки, разделенных часовыми промежутками, среднюю суточную величину данного элемента мы получим с такой точностью, которая далеко превосходит возможные ошибки наблюдений. Если обозначить величины, полученные ежечасными наблюдениями для данного элемента цифрами I, II, III, IV...XXIV, причем часы, как это принято в метеорологии, будут считаться от полуночи до полуночи, то, согласно сказанному, средняя суточная равна:
[I + II + III + IV +...+ (XXIV' + XXIV")/2]/24;
здесь XXIV' будет наблюдение в полночь, начинающую данные сутки, XXIV" — наблюдение в полночь, те же сутки заканчивающую. Совершенно аналогично этому можно найти среднюю за месяц величину данного элемента, суммируя все суточные С. и деля их сумму на число дней месяца; как среднюю из ежемесячных С., можно вычислить С. годовую. Можно далее искать С. для известного момента, суммируя все наблюдения, произведенные в этот момент, и деля сумму на число слагаемых. Наконец, имея наблюдения за большое число лет, можно искать из С. для каждого отдельного года среднюю многолетнюю или, как ее принято называть, среднюю нормальную, если число лет достаточно велико для того, чтобы средняя нормальная не меняла заметно своей величины, каковы бы ни были отдельные отклонения от нее. Получаемые таким образом С. представляют собой те нормы, около которых происходили за данный промежуток времени все колебания данного метеорологического элемента. Уклонения рассматриваемого элемента от средней могут быть очень велики; но средняя величина потому и является такой характерной, что сумма положительных от нее отклонений рассматриваемого элемента за некоторый промежуток времени всегда будет равна сумме его отрицательных от средней отклонений. Здесь приведены за каждый месяц и за год средние температуры для СПб., где имеется длинный ряд вполне надежных наблюдений, — а именно с 1743 г.; кроме того, приведены еще и наивысшие, и наинизшие С. за весь период наблюдений для каждого месяца и года, и величины отклонений для этих наивысших и наинизших от С.
| С.-Петербург — Температуры | |||||||
| За месяцы | Средняя температура | Наивысшая с 1743 г. | Отклонение от средней | Год | Наинизшая с 1743 г. | Отклонение от средней | Год |
| Январь Февраль Март Апрель Май Июнь Июль Август Сентябрь Октябрь Ноябрь Декабрь Год | —9,3° —8,5° —4,7° 2,1° 8,7° 14,8° 17,6° 16,0° 10,8° 4,5° —1,5° —6,5° 3,7° | —1,4° —1,1° 1,5° 7,5° 16,2° 19,7° 23,2° 19,7° 14,5° 9,3° 4,2° —0,3° 6,3° | +7,9° +7,4° +6,2° +5,4° +7,5° +4,9° +5,6° +3,7° +3,7° +4,8° +5,7° +6,2° +2,4° | 1882 1793 1836 1827 1897 1774 1757 1775 1775 1775 1772, 1877 1826 1826 | —21,4° —19,5° —10,8° —3,7° 2,1° 11,1° 14,0° 12,6° 7,1° —0,5° —10,0° —18,4° 1,1° | —12,1° —11,0° —6,1° —5,8° —6,6° —3,7° —3,6° —3,4° —3,7° —4,0° —8,5° —11,9° —2,6° | 1814 1871 1809 1790 1867 1810 1878 1835, 1856 1894 1880 1774 1788 1809 |
Средняя величина, будучи получена для некоторого элемента за определенный промежуток времени, является для той части метеорологии, которая изучает ход метеорологических элементов и их распределение по земной поверхности, — для климатологии — могущественным средством исследования. Сравнивая С. величины за отдельные промежутки времени между собой, метеорология получает возможность количественно оценивать изменения метеорологических элементов как в пространстве, так и во времени. Но этим значение С. величин для метеорологии не исчерпывается: в них эта наука имеет надежнейшее средство для отделения правильных, периодических изменений элементов погоды от изменений случайных, непериодических. Когда приходится иметь дело с таким сложным явлением как погода, в которой на изменения периодических элементов накладывается целый ряд изменений непериодических, то первой задачей должно явиться отделение периодических изменений от случайных, подведение тех и других под некоторые нормы — словом, необходимо дать для тех и других некоторые численные, количественные выражения. Но когда мы имеем дело с явлением, совершающим крайне неправильные колебания около некоторой нормы, то чем больше сделано наблюдений над изучаемым явлением для определения этой нормы, тем больше будет вероятность, что каждое резкое отклонение в одну какую-либо сторону будет уравновешено такой же величины отклонением или, по крайней мере, их рядом, но в сторону, обратную предшествующему. В этом накоплении наблюдений состоит закон больших чисел, применяемый теорией вероятности к случаям, подобным здесь рассматриваемому. В теории вероятностей выводится формула, данная Гауссом, для определения вероятной погрешности, которую может содержать некоторая средняя, выведенная из наблюдений, повторенных известное число раз. По этой формуле, если назовем через v отклонения (или резкости) для каждого наблюдения от средней, вероятная погрешность F найденной средней будет:
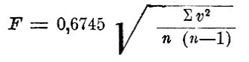
где Σ v2 будет обозначать сумму квадратов всех отклонений v отдельных наблюдений от средней. Если n очень велико, формула может быть еще упрощена и, по Фехнеру, в этом случае:
Эти формулы дают ответ на поставленный вопрос и позволяют определить, какое число лет нужно для получения нормальной средней с определенной степенью надежности. Если применить формулу Фехнера, например, к приведенным уже выше наблюдениям для СПб., то для определения нормальной средней температуры каждого месяца и нормальной С. за год с точностью до 0,1° Ц. нужно, по Вильду ("О температурах воздуха Российской Империи", СПб., 1878), не менее следующего числа лет наблюдений: для января 717 лет, для февраля 604 года, для марта 376 лет, для апреля 188 лет, для мая 168 лет, для июня 129 лет, для июля 153 года, для августа 127 лет, сентября 114 лет, октября 159 лет, ноября 265 лет, декабря 685 лет, для годовой 41 год.
Г. Любославский.
| "БРОКГАУЗ И ЕФРОН" >> "С" >> "СР" |
Статья про "Средние величины в метеорологии" в словаре Брокгауза и Ефрона была прочитана 1248 раз
| Бургер двойного помола |
| Яйца в кляре |
TOP 15
- Волос
- Проно
- Степные животные
- Гимнастика
- Индийский океан
- Архитектура
- Сравнение, в литературе
- Манда
- Клитры
- Колесование
- Испарение
- Травоядные животные
- Оплодотворение у pacтений
- Вредные насекомые
- Электризация тел