


БНБ
"БРОКГАУЗ И ЕФРОН" (121188)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Сопротивление материалов
Определение "Сопротивление материалов" в словаре Брокгауза и Ефрона
Сопротивление материалов
Сопротивление материалов*
— Когда, при составлении проекта сооружения или машины, форма, главные размеры частей и силы, которым они будут подвержены, уже определены на основании требований задания, данных механики и технологии, приходится еще определять остальные размеры так, чтобы эти части оказались прочными. Это определение и составляет главный предмет современного учения о С. материалов. Древние не оставили никаких данных относительно способов, которыми их зодчие определяли прочные размеры своих сооружений. Постройки древних отличались массивностью, им не было надобности соблюдать экономию в материале, и они могли довольствоваться примерами прежних построек. Строители средневековых готических храмов, с их легкими сводами и контрфорсами, вероятно, делали опыты и расчеты, но сведений о том, как это делалось, до нас не дошло. Первые основания научного исследования законов С. материалов положены Галилеем в 1638 г. Он установил, что наибольший груз, поддерживаемый брусом, свободно лежащим на двух опорах, пропорционален ширине и квадрату вышины и обратно пропорционален длине. Гук, в 1678 г., нашел, что упругие растяжения пропорциональны силам. Затем Мариотт, выработавший представление о нейтральном слое в изгибающемся бруске, заметил, что он находится на средине высоты бруса симметричного сечения, но сделал ошибки в дальнейшем выводе формул. В течение столетия после этого многие ученые без успеха затрагивали тот же вопрос, и только в 1807 году Юнг решил его для случая "простого гнутия" бруса симметричного сечения, введя в первый раз понятие "о модуле упругости", а в 1824 г. Навье дал уже полное решение. Дальнейшее развитие, как теоретическое, так и экспериментальное, учения о С. материалов пошло очень быстро, так как им были заинтересованы почти все выдающиеся представители инженерного дела и физики. В настоящее время разработано для целей практических учение о С. материалов и, независимо от него, научная теория упругости. Приемы первой заведомо логически неправильны: в ней формулы метода бесконечно малых применяются к малым, но конечным изменениям формы. Поэтому все выводы получаются лишь приблизительными, но требования практики, как увидим, так поставлены, что достигаемое приближение вполне достаточно, тем более, что результаты таких вычислений было многократно проверены опытом, и вне пределов этой проверки не применяются.
При рассмотрении условий равновесия сил, приложенных к фиктивному "неизменяемому телу", две равные силы, действующие в обратные стороны вдоль одной прямой, взаимно уравновешиваются, независимо от того, действуют ли они в одной и той же точке или в двух разных. Когда же рассматривается действительное тело, одаренное упругостью, дело усложняется: частицы, к которым непосредственно приложена внешняя сила, изменяют настолько свое положение относительно других, что развивающиеся вследствие этого междучастичные силы упругости уравновесят ее; вместе с тем упругое противодействие от частицы к частице передает усилие до точек приложения сил, уравновешивающих первую. При этом изменяются и размеры, и форма самого тела. Опыт показал, что пока изменения эти очень малы, они исчезают, как только силы, их производящие, перестают действовать, а величины этих изменений, при равных прочих условиях, оказываются пропорциональными действующим силам. Когда же силы и производимые ими изменения постепенно возрастают, сначала изменения эти перестают исчезать вполне, когда силы прекращают свое действие, а затем достигается и такая нагрузка, что тело разрушается. Наименьшая нагрузка, оставляющая после себя "остаточную деформацию, соответствует "пределу упругости", а вторая, "пределу прочности" рассматриваемого материала. Нагрузки, которые входят в формулы С. материалов, никогда не доходят до предела упругости; поэтому-то производимые ими конечные, но очень малые изменения размеров можно считать как бы бесконечно малыми и применять к выводу соответственных формул методы дифференциального и интегрального исчисления, а также закон независимости действия сил. Относительно этого закона вопрос поставлен следующим образом: целью учения о С. материалов служит вычисление "прочных" размеров тел, данной формы, сделанных из известных материалов и подверженных данным силам, а для этого обыкновенно необходима неизменяемость формы такого рода тел, под влиянием сил на них действующих. Исключение составляют лишь пружины (см.), а немногие гибкие части машин, веревки ремни и т. п. тоже выбираются так, чтобы их длина не изменялась заметно. Поэтому-то можно сначала рассмотреть простейшие элементарные случаи деформации вещества твердого тела: растяжение, сжатие, сдвиг, гнутие (изгиб) и кручение, а все более сложные деформации рассматривать, как сложившиеся из простых. Так, если действуют две растягивающие силы, окончательное растяжение можно считать суммой растяжений, которые произвела бы каждая сила, действуя в отдельности. Этот способ рассуждения, очевидно, неточен: ведь по закону действия упругих сил от действия второй силы возрастет и первоначальная длина тела, и ее приращение, вызванное первой силой. Однако, при очень малых приращениях, приращение приращения будет практически ничтожно. Для практики обыкновенно не требуется даже знать величину деформации, нужна лишь уверенность, что при вычисленных размерах предмет не разрушится под влиянием предполагаемых сил. Опыт показал, что для этого необходимо, чтобы ни в какой точке внутренний натяжении не превосходили той величины, которая соответствует пределу упругости; смотря по роду материала и сооружения, принято допускать лишь нагрузки, ни в каком случае не превышающие половины этой величины. Такой "запас прочности" вполне покрывает погрешности, допускаемые при вычислениях. Для решения практических вопросов о С. материалов нужны и формулы, и знание свойств употребительных материалов, полученное из опыта. Так как постановка этих опытов приноровлена к формулам, служащим для вычисления их результатов, то необходимо познакомиться сначала с формулами. Рассмотрим элементарные деформации, на которые можно разлагать более сложные деформации.
1) Растяжение или сжатие под влиянием равномерно распределенной нагрузки. В таких условиях находится, например, проволока или прут, на котором висит груз, стены парового котла, камень в стене и т. п., в частях, достаточно удаленных от точек приложения внешних сил или от скреплений. В таком случае, если назвать поперечное сечение (в кв. стм) буквой S, a силу, действующую на него в нормальном направлении (в кг), буквой Р, нагрузка на кв. стм, T, получится от разделения P на S. Опыты показали, что растяжение оказывается пропорциональным длине L (стм), если рассматриваемая часть имеет по всей своей длине одинаковое сечение и однородное строение материала. Коэффициент этой пропорциональности определяется обыкновенно "модулем упругости" (введенным в науку Юнгом), обозначаемым обыкновенно буквой E; величина эта тем больше, чем материал упруже, поэтому удлинение
l = L[P/(ES)].
Значит, удлинение пропорционально длине, отношению силы к поверхности сечения, на которую они действуют, и обратно пропорционально числу E, характеризующему материал. Формула эта одинаково применяется и для малых растяжений, и для малых сжатий, вызываемых сравнительно небольшими нагрузками на каждый квадратный стм поверхности сечения. Если бы применимость этой формулы не ограничивалась очень малыми растяжениями l, то E равнялось бы нагрузке на кв. стм Т = Р:S, производящей растяжение l = L, длине растягиваемого тела. На деле E вычисляют, измерив очень маленькое растяжение l и соответствующие ему L, P и S; получаются обыкновенно очень большие числа, имеющие вышеуказанный смысл [К. Бах вводит вместо E величину обратную: коэффициент удлинения α, т. е. удлинение каждого сантиметра тела сечения 1 кв. стм от нагрузки в 1 кг]. Опыты показали, что, при последовательном увеличении нагрузки T доходят до такой ее величины T е , при которой тело уже не возвращается к своей первоначальной длине L, когда усилие перестает действовать. Эту нагрузку Те считают мерой "предела упругости" рассматриваемого вещества. Если после получения "остаточной деформации" снова нагрузить то же тело до степени, не превышающей Те, то новой остаточной деформации не получается, а коэффициент упругости, отнесенный к начальной длине, остается почти без изменении (слегка возрастая). При дальнейшем увеличении нагрузки, для материалов хрупких, явление идет тем же порядком до предела прочности — нагрузки Т r, — при которой сразу происходит разрыв или разрушение от сжатия. Для тел же вязких, типом которых может служить мягкая сталь, раньше разрыва начинается сильное растяжение или сжатие, сопровождаемое обратным изменением поперечного сечения, продолжающееся без остановки и прибавки нагрузки, до полного разрушения. Условием прочности будет в этих двух случаях требование, чтобы нагрузка не превышала не только предела прочности, но даже предела упругости материала. Обыкновенно допускают нагрузку Т кг на кв. стм лишь в половину "предела упругости", или, что почти то же, в одну четверть "предела прочности" материала; но во многих частных случаях, особенно когда нагрузка не постоянная, а переменная, или когда она быстро, периодически меняет свое направление, приходится допускать еще меньшие нагрузки, установленные специальными опытами.
2) Сдвиг, производится срезывающим усилием, когда на два параллельных между собой сечения тела действуют две равные, параллельные между собой силы противоположного направления, заключенные в плоскостях соответственных сечений. Срезывающему усилию подвергаются, напр., заклепки, соединяющие наложенный один на другой края листов парового котла или части балки (см.). На фиктивное "неизменяемое твердое тело" такие две силы производили бы одно только вращательное усилие, действовали бы лишь как "пара сил"; будучи же приложены к действительному телу, подверженному упругим частичным изменениям, они, сверх того, производят сдвиг одних слоев частиц относительно других.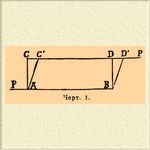
Черт. 1.
Наглядное представление о роде такого перемещения частиц можно получить следующим путем: представим себе еще не перелистанную, брошюрованную и обрезанную книгу (черт. 1), лежащую на столе: ее сечение ABCD, нормальное к длине корешка, представит прямоугольник. Если же мы, задерживая нижнюю поверхность книги этой на столе, потянем за верхний лист обложки, по направлению СР, перпендикулярному к корешку и параллельному поверхности стола, то книга скосится, ее сечение из прямоугольника обратится в параллелограмм ABC'D', причем расстояние между двух длинных сторон не изменится. Листки книги при этом будут равномерно сдвинуты один относительно другого. Мерой сдвига будет служить тангенс угла САС' между стороной начального прямоугольника и наклонной стороной параллелограмма, в которую она перешла, или равное ему отношение перемещения СС' к расстоянию АС плоскостей приложения сил Р, Р. Сдвиг, растяжение и сжатие постоянно сопровождают друг друга: когда параллельно одной плоскости совершается сдвиг, в других плоскостях происходят сжатия и растяжения. Так, при переходе прямоугольника ABCD в параллелограмм, диагональ AD удлинилась, а ВС укоротилась; при сжатии, в сечении, нормальном к направлению силы, происходит одно лишь сжатие, а в каждом наклонном сечении относительное перемещение частиц будет сложено из сжатия и скольжения, вследствие чего при разрушении от сжатия получаются наклонные трещины и тело распадается на неправильные клинообразные куски. При сдвиге, зависимость между нагрузкой и производимым ею сдвигом частиц подобна зависимости при растяжении: модуль сдвига, G = 2/5E модуля упругости, а предельная нагрузка, производящая разрыв при срезывании, равна 4/5 соответственной нагрузки при растяжении.
3) Простое гнутие. Когда прямой брусок AB (черт. 2) закреплен одним концом, а на другой действует сила Р, направленная перпендикулярно к длине бруска, сила эта производит одновременно и сгибающее усилие, и срезывающее.
Черт 2.
Действительно, в произвольно выбранной точке можно приложить взаимно уничтожающиеся силы P и — Р; данные силы + Р и — P образуют пару сил, стремящуюся повернуть часть ВС относительно части СА, тогда как сила P будет производить срезывающее усилие в сечении, проходящем через С. Под влиянием этих сил развиваются соответственные силы упругости, и наступит равновесие или излом, смотря по тому, будет ли где-либо превзойдено прочное сопротивление или нет. Можно выбрать такое распределение внешних сил, что в некоторой части бруска срезывающее усилие будет равно нулю, а сгибающий момент станет постоянным во всех точках: тогда осуществится "простое гнутие". Для этого следует положить брусок на подставки А и B (черт. 3), на расстоянии АВ = l, и нагрузить свешивающиеся концы равными грузами P на равных расстояниях а от опор.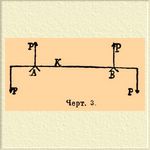
Черт. 3.
В таком случае, на брусок будут действовать две пары сил, с моментом Ра, стремящиеся повернуть концы бруска в противоположные стороны и сгибающие его, вызывая противодействующие упругие силы, уравновешивающие сгибающий момент. При этом в верхней части бруска будет происходить растяжение, а в нижних сжатие; где-то посредине его поперечного сечения будет место слоя, где нет ни растяжения, ни сжатия: это будет "нейтральный слой". Никакого срезывающего усилия в части бруска между точками опоры не будет: обе силы P гнут в одну сторону; самый же момент этих сил в части AB будет постоянным. Если сечение бруска и его строение тоже постоянно, то и гнутие будет постоянным во всех точках, т. е. прямой брусок изогнется по дуге круга. В этом случае нетрудно вычислить, какие силы упругости разовьются в каждом произвольно выбранном нормальном сечении бруска и уравновесят гнущий момент внешних сил. Если рассматривать сначала продольное, вертикальное сечение бруска между опорами А и В (черт. 4), то окажется, что прямолинейные слои стали дугами концентрических кругов.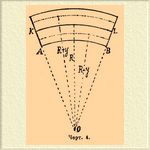
Черт. 4.
Назвав (обыкновенно очень большой) радиус нейтрального слоя буквой R, можно будет обозначать через R+ у или R—у радиус каждого слоя, находящегося на у выше или ниже нейтрального. До сгибания все эти слои, заключавшиеся между двумя вертикальными параллельными сечениями бруска, были равной длины, после сгибания каждый из них стал дугой круга, соответствующей одному и тому же углу, но разного радиуса; значит, по сравнению с нейтральным слоем радиуса R, каждый получил ± приращение длины пропорциональное своему расстоянию у от нейтрального слоя, так как дуги, соответствующие тому же углу, пропорциональны своим радиусам. Мы назвали уже буквой Е коэффициент упругости: нагрузку на единицу поверхности, которая уравновесила бы упругие силы, вызванные удвоением длины, если бы такое растяжение было возможно — значит, упругие силы T, развивающиеся на единицу поверхности в слое на расстоянии у от нейтрального, будут удовлетворять пропорции: Т: Е = у:R.
Рассмотрим теперь поперечное сечение бруска между его опорами, нормальное к его длине; на него, как было уже указано, действует лишь сгибающий момент, постоянный для всех точек, а равнодействующая всех внешних сил равна нулю во всех точках. После простого изгиба каждое из этих сечений, оставаясь плоским, так повернется, что станет проходить чрез общий центр кривизны, о, всех изогнутых слоев бруска. До нагрузки правая и левая часть были связаны силами сцепления; после изгиба в верхней части развиваются силы, притягивающие обе половины одну к другой, а в нижней — силы, их отталкивающие. Суммы всех этих вновь развившихся сил должны быть равны нулю, когда наступило равновесие, потому что сумма всех внешних сил равна нулю. Это условие позволяет определить положение нейтрального слоя, при посредстве обыкновенного приема исчисления бесконечно малых. Представим себе (черт. 5), что все поперечное сечение разделено на бесконечно узкие полоски высотой в Δ y, a шириной b, во все сечение.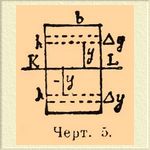
Черт. 5.
Так как эта полоска поверхности на расстоянии у от нейтрального слоя, то натяжение на единицу поверхности в ней будет g = Еу /R, а натяжение на поверхность полоски будет [(Еу)/R]b Δ y. Если взять сумму всех таких выражений для всей поверхности поперечного сечения, принимая во внимание знаки у, должно получиться выражение равное нулю: (E/R) Σ by Δ y = 0. Но известно, что эта сумма равна нулю, если линия, от которой считаются координаты у, проходит через центр тяжести: этим признаком ведь определяется положение центра тяжести плоской фигуры. Поэтому "нейтральная ось, при простом гнуmuu, проходит через центр тяжести нормального поперечного сечения".
Те же упругие силы уравновешивают и сгибающий момент Ра относительно линии KL, проходящей через нейтральный слой. Если сила, действующая на элемент поверхности, b Δ у равна (E/R) уΔ у, то ее момент равен (E/R) у 2b Δ у, а для всего сечения (E/R) Σ у 2b Δ у, т.е.
Pа = (E/R) Σ у 2b Δ у = (E/R)J
если назвать буквой J "момент инерции" сечения бруса относительно горизонтальной оси, проходящей чрез его центр тяжести (см. соотв. статью).
Отношение Е: Е можно заменить отношением T:y.
Рa = (TJ)/y
Для прочности Т не должно превышать предела упругости, разделенного на коэффициент, выражающий "запас прочности", для слоя наибольше удаленного от центра тяжести. Назвав наибольшее значение у чрез h (в зависимости от формы сечения оно может быть направлено и вниз, и вверх от центра тяжести), получим: P = (TJ)/(ha).
4) Кручение. В этом случае происходит лишь сдвиг одних частиц относительно других, только величина этого сдвига неодинакова для разных мест одного и того же сечения. Представим себе (черт. 6), что цилиндр длиною l закреплен с одного конца и что к другому его концу, в плоскости, перпендикулярной к оси, приложен скручивающий момент М, повернувший эту плоскость на дугу θ . Выделим мысленно трубчатый цилиндр, концентрический с данным, той же длины, но радиуса r, с ничтожной толщиной стенок Δ r, и развернем этот цилиндр в плоскость. До скручивания он представил бы прямоугольник (см. черт. 7), длиной AB и шириной 2π r; после скручивания он обратится в параллелограмм, мерой сдвига будет служить BAB = (r θ)/l.
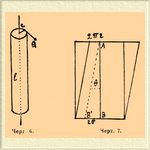
Черт. 6. Черт. 7.
Назвав модуль сдвига G, получим для срезывающего усилия на единицу поверхности: F = (Gr θ)/l, а для пластинки сечения 2π r Δ r, момент
Δ M = 2 π r Δ rG[(r θ r)/l] = [(2 π G θ)/l]r3 Δ r.
Чтобы найти момент для сплошного цилиндра радиуса r, надо взять сумму всех таких выражений для трубчатых цилиндров с радиусами, уменьшающимися на Δ r от R до 0. Это делается по правилам интегрального исчисления, заменяя конечное приращение Δ r дифференциалом r. Так как силы упругости уравновешивает момент внешних сил, то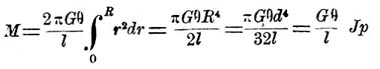
где d = 2R, Jp — полярный момент инерции сечения цилиндра. Отсюда можно вывести:
θ = (Ml)/(JpG) и G = (Ml)/(Jp θ).
Модуль упругости сдвига G обыкновенно определяется из опыта посредством наблюдения угла кручения и момента сил его производящего. Равенство: G = 2/5E выведено на основании теоретических соображений для тела однородного строения; опыт дает для реальных тел другие отношения, но довольно близкие к теоретическому. Для прочности, натяжение на единицу поверхности, F, не должно ни для одного места превосходить предела упругости, разделенного на принятый коэффициент прочности. Наибольший сдвиг будет, очевидно, на поверхности цилиндра, когда r = R; будем искать, какая сила Р, приложенная на самую поверхность цилиндра, произведет в этом месте наибольшее допустимое напряжение Т. В таком случае момент М = РR = G (θ /l)Jp, но напряжение на единицу поверхности F = G(θ /l)r, для нашего случая, обратится в Т = (G θ /l)R; из этих двух формул, исключив G θ /l, получим:
G θ /l = PR/Jp = T/R; P = TJp/R2.
Учение о С. материалов доказывает некоторые общие теоремы, имеющие приложения. Так: два геометрически подобных тела, из одного и того же материала, подверженные действию подобно расположенных сил, пропорциональных квадратам сходственных измерений, оказывают одинаковую прочность. Этим правилом можно руководствоваться, чтобы по модели сделать соображения о действии настоящей машины или ее части. Надо, однако, помнить, что собственный вес не принимается тут в соображение; когда же он значителен по сравнению с внешними силами, — правило не применимо, так как вес возрастает пропорционально кубам сходственных измерений, т. е. в k раз быстрее, чем предполагается, и большой, тяжелый предмет менее прочен, чем ему подобный меньший. В такой же мере превысит прочность и центробежная сила предмета в k раз большего, делающего то же число оборотов в минуту.
В действительных случаях обыкновенно нагрузки действуют так, что происходят единовременно разные простые деформации; чтобы вычислить окончательную деформацию, надо, как было указано выше, вычислить простые деформации отдельно и затем сложить их по правилам сложения единовременных перемещений. Но вычисление наибольшей допустимой нагрузки делается обыкновенно гораздо проще: оказалось обыкновенно, что наибольшие деформации разных родов происходят в разных местах тела; напр., при гнутии силой, действующей на конце заделанной балки, наибольшее растяжение в верхнем слое, наибольшее сжатие в нижнем, а наибольшее скольжение в нейтральном слое, где ни сжатия, ни растяжения не происходит. Поэтому, вычислив наибольшие напряжения разного рода, остается лишь выбрать размеры, удовлетворяющие наибольшему из них. На основании такого рода соображений вычислена прилагаемая таблица нескольких самых обыкновенных случаев.
Моменты инерции и поверхности употребительных форм сечений балок (J момент инерции относительно горизонтальной линии, проходящей через центр тяжести фигуры. Jp полярный момент инерции относительно оси, проходящей чрез центр тяжести; h наибольшее вертикальное расстояние центра тяжести от окружности сечения; все размеры в стм).
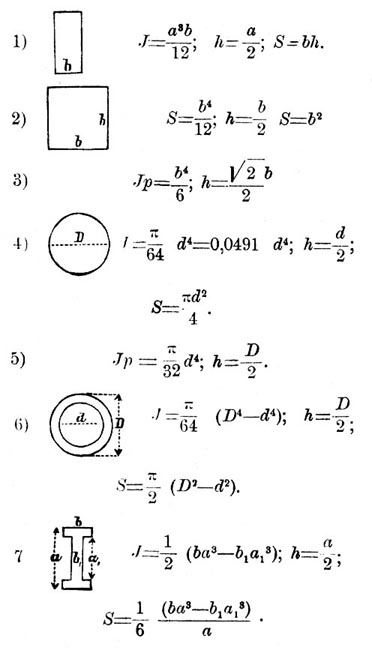
Часто встречающиеся случаи нагрузок балки равномерного сечения (Длина l стм, груз Р кг в одной точке или P = ql кг, распределенным равномерно по всей длине l, момент инерции J, расстояние центра тяжести h стм, прочная нагрузка Т кг на 1 кв. стм, момент груза М, полярный момент инерции Jp).
1) Балка заделана одним концом, груз P на свободном конце: М = Рl, Р = (TJ)/(lh); опасное сечение у заделки.
2) Тот же случай, но груз распределен равномерно: М = Рl /2 , Р = 2(TJ)/(lh); опасное сечение там же.
3) Балка свободно лежит обоими концами на опорах, груз на середине: М = Рl /4 ; Р = (4TJ)/(lh); опасное сечение на средине.
4) Тот же случай, но груз распределен равномерно: М = Рl /8, Р = (8TJ)/(lh); опасное сечение на средине.
5) Тот же случай, но груз на расстояниях с и c1 от концов:
M = (Pcc1)/l; P = [l/(cc1)][(TJ)/(lh)]; опасное сечение в точке приложения груза.
6) Балка, заделанная обоими концами, груз на средине: M = (Pl)/8; Р = (8TJ)/(lh); опасное сечение на заделанных концах.
7) Тот же случай, но груз распределен равномерно по всей длине: M = (Pl)/12; Р = (12TJ)/(lh); опасное сечение на концах.
8) Балка опирается в двух точках и нагружена двумя грузами P на свободных концах, свешивающихся на равные длины а (случай равномерного, простого сгибания). М = Рa, для всех точек между опорами, Р = (TJ)/(ah); опасным сечением может считаться всякое сечение между опорами.
9) Балка, закрепленная одним концом, подвержена на свободном конце скручивающему моменту PR. Усилие: P = (TJp)/(hR); угол скручивания Δ = (PRl)/(JpG) = (T/G)(l/h); опасное сечение может считаться безразлично всякое (G означает модуль сдвига).
10) Подпорные столбы круглого сечения вычисляются, как подверженные одному сжатию, когда их длина не превышает диаметр более чем 10 раз для чугуна, в 24 раза для железа, и в 11,5 раз для дерева; концы предполагаются незакрепленными. Когда же столб более тонок — пользуются приблизительной, проверенной опытами формулой, выведенной в предположении, что столб уже изогнулся по дуге круга: Р = (π 2/k)(JE/l2) (Е модуль скорости). Запас прочности, 1/k, берут от 1/6 до 1/4, для чугуна и железа, и от 1/12 до 1/10 для дерева.
Таблица допускаемых нагрузок Т в кг на 1 кв. стм, по Баху (а — постоянная нагрузка, b — переменная, с — меняющая свое направление).
| Растяжение | Сжатие | Изгиб | Кручение | |||||||||
| а | b | с | а | b | с | а | b | с | а | b | с | |
| Железо сварочное | 900 | 600 | 300 | 900 | 600 | 300 | 900 | 600 | 300 | 360 | 240 | 120 |
| Железо литое | до 1200 | 800 | 400 | 1200 | 800 | 400 | 1200 | 800 | 400 | 840 | 560 | 80 |
| Сталь литая, мягкая | до 1500 | 1000 | 500 | 1500 | 1000 | 500 | 1500 | 1000 | 500 | 1200 | 800 | 400 |
| Чугун *) | 300 | 200 | 100 | 900 | 600 | 300 | от 435 до 615 | 200 410 | 145 205 | — | — | — |
| Сосновое дерево | 100 | — | — | 60 | — | — | — | — | — | — | — | — |
| Дубовое дерево | 100 | — | — | 80 | — | — | — | — | — | — | — | — |
| Кирпичная кладка | — | — | — | 7 | — | — | — | — | — | — | — | — |
| Кирпичная на цементе | — | — | — | 12 до 14 | — | — | — | — | — | — | — | — |
| Бетон | — | — | — | 12 | — | — | — | — | — | — | — | — |
*) Для чугуна числа наибольшие, когда литейная кора снята и сечение круг; наименьшая для неотделанных брусьев ребристого сечения. Для разных сортов Т меняется в отношении 1:4.
Опыты и численные данные. Для успешного пользования формулами С. матер. надо было узнать на основании опыта свойства употребительных материалов, какие коэффициенты прочности необходимо брать в разных случаях, какие прочные нагрузки выдерживают различные, употребительные материалы. Практика показала, что размеры, определяемые по правилам С. материалов, оказываются обыкновенно правильными для крупных сооружений и машинных частей, а для очень малых частей размеры эти выходят слабыми, и их необходимо увеличивать по соображению. Это происходит вследствие влияния посторонних, случайных усилий, не принимаемых во внимание при расчете, но часто превосходящих усилия, полагаемые в его основание, когда они малы. Свойства разных продажных сортов материала того же наименования оказываются очень различными, так что при сооружениях, подверженных большим нагрузкам, где невозможно допустить большой запас прочности, приходится определять прочное С. из опытов, сделанных над пробами того самого материала, который идет в дело. Для этой цели существует много типов машин, постоянно применяемых при постройках мостов и механизмов, а также на металлургических заводах. Свойства строительных материалов так разнообразны, что еще далеко не вполне исследованы в наше время; всего важнее знать прочную нагрузку, предел упругости и удлинение при растяжении и сжатии. Непосредственное определение соответственных величин для сдвига делается сравнительно редко, потому что значительному сдвигу частиц подвергаются лишь заклепки и валы (см.), передающие рабочую силу в фабричных трансмиссиях и на пароходах; в других же случаях главные деформации сводятся к растяжениям и сжатиям. Коэффициент прочности в одну четверть предела прочности признается вполне достаточным для металла, когда нагрузка постоянна или изменяется плавно. Но бывают части машин, нагрузка которых при каждом обороте некоторого вала много раз в минуту возрастает на некоторую величину и опять уменьшается, или же переменяет свое направление; в первом случае допускают лишь одну шестую, во втором — одну двенадцатую предела прочности. В этих случаях материал пластический, способный сильно вытягиваться до разрыва, допускает меньший запас, чем материал разрывающийся без большого растяжения. Однако, при тех же размерах, материал более хрупкий, но имеющий значительно больший предел прочности, может оказаться абсолютно более прочным. Для дерева, подверженного гниению, берут десятерной или восьмерной запас прочности, а для камня — не менее десятерного, потому что материал этот очень неравномерного строения. На предел прочного С. очень влияет время и температура. Давно известно, что нагрузка, при продолжительном действия разрушающая нагруженный предмет, не произведет порчи, действуя лишь непродолжительное время, вследствие чего для временных сооружений допускается половинный запас прочности. Это частный случай явления, называемого в физике "упругим последействием" (см.) и заключающегося в том, что упругие деформации требуют времени, чтобы совершиться вполне. Явление это особенно заметно на материалах органического происхождения, шелке, шерсти, каучуке, дереве и т. п. Строительные материалы тоже ему подвержены, но в малой степени; однако, при возвышенной температуре, действие больше. Так, цинк с течением времени сильно деформируется, если он подогрет, а закаленная стальная пружина постепенно все больше и больше поддается действию одной и той же небольшой нагрузки, при температурах от 100° до 300°C, соответствующих разной степени "отпускания" (см.) и, не теряя своей закалки, сохраняет после этого остаточные изменения формы. При нагревании незакаленной мягкой стали и железа (по опытам Лешателье), сначала их предел прочности изменяется мало, около 200°C он начинает быстро возрастать, а с 300°C опять сильно понижается. Но уже с 50°С начинает уменьшаться растяжимость железа и стали и только к 300°С получает опять величину, близкую к прежней. Если растяжение, переходящее за предел упругости, действует продолжительное время или много раз повторяется, то оно ведет к разрушению, но однократное растяжение, немного переходящее за предел упругости, лишь увеличивает несколько предел прочности тягучего материала, уменьшая при этом степень его тягучести. Свойство это много облегчает сборку частей, особенно грубо пригнанных и соединенных заклепками: во многих местах получаются чрезмерные напряжения, которые сами собой сглаживаются, потому что нагрузка в этих местах превосходит предел упругости и материал понемногу подается, вследствие чего напряжения уменьшаются. От продолжительного действия большой нагрузки, переменной и сопровождаемой толчками, металлические части "устают" и предел их прочности значительно понижается. Это замечается особенно на осях вагонов. Правильное отжигание восстановляет прежние свойства металла; есть даже указание, требующее подтверждения, что усталый материал может отдохнуть и от одного лежания вновь получить прежние свойства: один американский практик пишет, что лезвие очень хорошего зубила стало быстро тупиться от ударов в его руках после очень продолжительной непрерывной работы, но прежнее качество лезвия восстановилось через несколько дней, когда он дал этому зубилу отдохнуть, по совету старого мастера. Машины для пробы материалов, по существу своего назначения должны содержать орган, производящий усилие, средство для измерения этого усилия и приспособления для соответственного опыту закрепления исследуемого образца. К этому присоединяются часто самозаписывающий прибор и приспособления для точного измерения деформаций во время опыта. Для целей практических, опыт должен совершаться скоро и легко, а для разных научных целей требовались многоразличные усложнения; поэтому в настоя
| "БРОКГАУЗ И ЕФРОН" >> "С" >> "СО" >> "СОП" |
Статья про "Сопротивление материалов" в словаре Брокгауза и Ефрона была прочитана 1816 раз
| Креветки с газировкой |
| Креветки с газировкой |
TOP 15
- Волос
- Проно
- Степные животные
- Гимнастика
- Индийский океан
- Архитектура
- Сравнение, в литературе
- Манда
- Клитры
- Колесование
- Испарение
- Травоядные животные
- Оплодотворение у pacтений
- Вредные насекомые
- Электризация тел