


БНБ
"БРОКГАУЗ И ЕФРОН" (121188)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Солнечная радиация
Определение "Солнечная радиация" в словаре Брокгауза и Ефрона
Солнечная радиация
Солнечная радиация
— Все процессы на поверхности земного шара, — каковы бы они ни были, — имеют своим источником солнечную энергию. Изучаются ли процессы чисто механические, процессы химические в воздухе, воде, почве, процессы ли физиологические или какие бы то ни было вообще, — первичной причиной всех их без исключения оказывается Солнце. Во всех этих процессах происходит только одно из превращений той начальной энергии, которую посылает на Землю в виде своих лучей это центральное светило нашей планетной системы. В сравнении с этим основным источником энергии, потребляемой земным шаром, другие ее источники: излучение звезд, собственная теплота Земли, различные космические процессы, — все они величины бесконечно малые. Поэтому вопрос о количестве энергии, проникающей на земную поверхность от Солнца, есть основной вопрос всей физики земного шара, — метеорологии. Вся эта наука — не что иное, как изучение и подсчет прихода и расхода, актива и пассива энергии, получаемой Землей от Солнца. Под термином "солнечная радиация" и разумеют обыкновенно ту энергию, которую излучает Солнце и которая, будучи перехвачена земным шаром, и является на этом последнем первичным источником, — primum mobile, — всех явлений и процессов неорганического и животного миров. — Не будь земная поверхность защищена от непосредственного действия солнечных лучей воздушной оболочкой, облекающею ее мощным слоем до нескольких сот километров толщиной, изучение той части С. радиации, которая приходится на долю Земли, было бы делом очень несложным. Измерив раз только в определенный момент и в определенном месте напряженность С. радиации, мы могли бы уже затем при помощи элементарно простых формул предвычислить количество энергии в любой момент и в какой угодно точке земного шара. Присутствие атмосферы, обладающей свойством поглощать в весьма заметной степени солнечные лучи, — и притом различные лучи весьма неодинаково, — значительно усложняет дело. Допустим сначала, что атмосфера обладает совершенною прозрачностью и что, следовательно, до земной поверхности доходит целиком вся та энергия, которая перехватывается земным шаром. Так как количество энергии, получаемое данной поверхностью, пропорционально синусу угла, составляемого падающим пучком лучей с принимающей поверхностью, то основным элементом, определяющим интенсивность радиации на земной поверхности для любого пункта, будет высота Солнца над горизонтом; ею определится не только напряжение лучей в данный момент, но и вся сумма энергии, полученная единицей земной поверхности за определенный промежуток времени, может быть вычислена по высотам Солнца. Соответственно изменению высоты Солнца над горизонтом в течение суток, суточный ход С. радиации будет весьма прост. От момента восхода Солнца радиация быстро возрастает с поднятием светила над горизонтом; затем, достигнув довольно значительной величины, она начинает меняться более медленно, пока около полудня не достигнет максимума. После полудня кривая радиации совершенно симметрично опускается сначала медленно, затем ближе к закату Солнца весьма быстро. Так как с изменением широты места для одного и того же дня будут изменяться полуденные высоты Солнца и продолжительность дня, то получаемое в течение суток количество энергии зависит от широты места. Количество получаемой от источника данной поверхностью энергии будет, далее, обратно пропорционально квадратам расстояний этой поверхности от источника. Поэтому годовой ход С. радиации для одного и того же места определится не только полуденными высотами Солнца и продолжительностью дня, изменяющимися в зависимости от времени года, но еще и расстоянием Земли от Солнца. На экваторе продолжительность дня и ночи в течение всего года одна и та же; количество энергии, получаемое единицей земной поверхности за сутки, будет здесь наибольшее в равноденствия, когда полуденное Солнце стоит в зените места, наименьшее в солнцестояния, когда высоты Солнца в полдень уменьшаются до 66°33'. Так как, сверх того, расстояние Земли от Солнца в перигелии и афелии не одинаковы, то в годовом ходе радиации здесь будут два минимума неодинаковой величины в солнцестояния и два максимума в равноденствия. Июньский минимум, соответствующий наибольшему расстоянию Земли от Солнца, будет значительнее, нежели декабрьский, падающий на ближайшее расстояние между Солнцем и Землей. Можно было бы, соответственно этому, думать, что количества энергии, получаемые Землей от сентябрьского до мартовского равноденствия будет больше, нежели получаемое от мартовского до сентябрьского равноденствия. Однако, это — не так: большее удаление Земли от Солнца в афелии (март — сентябрь) уравновешивается большей его продолжительностью (от мартовского до сентябрьского равноденствия — 186 дней), тогда как другое полугодие, соответствующею меньшему расстоянию между Землей и Солнцем, короче (между сентябрьским и мартовским равноденствиями — 179 дней). Количества энергии, получаемые Землей за оба полугодия, оказываются таким образом близко равными. При удалении от экватора к северу нетрудно убедиться, что декабрьский минимум будет все более и более углубляться по мере уменьшения полуденных высот Солнца и продолжительности дня, а июньский минимум постепенно будет делаться все менее и менее заметным; максимумы от моментов равноденствия будут сближаться между собой, пока не сольются в один общий, приходящийся на июнь. При этом оказывается; что по вычислениям количество энергии, получаемое в летний день единицей поверхности Земли за сутки, будет по мере удаления от экватора возрастать; это является, впрочем, совершенно понятным, так как с удалением от экватора возрастает и продолжительность летнего дня. На полюсе, наконец, где Солнце в течение целых шести месяцев остается над горизонтом, количество энергии, получаемой единицей земной поверхности в летний день, будет наибольшее, так как Солнце светит здесь все 24 часа. Кривая годового хода С. радиации от момента весеннего равноденствия будет здесь быстро возрастать до летнего солнцестояния и затем столь же быстро падать с приближением к осеннему равноденствию. То же самое, — только с обратным расположением максимумов и минимумов, — будет иметь место в годовом ходе и для южного полушария. Если, теперь, от сделанного допущения о полной прозрачности атмосферы для солнечных лучей перейти к действительности, то из наблюдений оказывается, что до земной поверхности доходит только некоторая часть той энергии, которая приносится лучами на пределы атмосферы; остальное поглощается самой атмосферой. Если обозначить через 1 все количество энергии, приносимой солнечными лучами, то до земной поверхности только в наилучшем случае дойдет часть, не превосходящая 0,8. Принято вообще отношение количества энергии, дошедшей до земной поверхности, к тому количеству, которое в действительности падает на пределы атмосферы, называть коэффициентом прозрачности атмосферы. Количество энергии, поглощаемое атмосферой, будет зависеть от массы воздуха, пройденной лучом; а эта последняя будет тем больше, чем длиннее путь, проходимый лучами в атмосфере и чем плотнее слои проходимого воздуха. Следовательно, поглощение лучей атмосферой будет тем больше, чем меньше высота Солнца над горизонтом. Масса воздуха, проходимая лучами, может быть вычислена по формуле Ламберта:
е = √h 2 + 2rh + r2Cos2z — rCosz,
где е — длина пути, проходимого солнечным лучом в атмосфере, h — высота атмосферы, которая может быть принята за единицу, r — длина радиуса земного шара и z — зенитное расстояние Солнца. Когда масса воздуха, встречаемого лучом, или, — что то же, — длина его пути известна, количество лучей, дошедшее до поверхности Земли, определится по закону Бугера (Bouguer), по которому "для среды с известным коэффициентом прозрачности количества прошедшей через нее энергии убывают в прогрессии геометрической, тогда как массы проходимой лучом среды возрастают в прогрессии арифметической". Если обозначить через i — количество энергии у поверхности Земли, чрез J — то же количество у предела атмосферы, d — коэффициент прозрачности атмосферы и е — массу атмосферы, то, по закону Бугера
i = Jpe
На основании этого закона, зная р, можно вычислить, каков будет ход С. радиации в присутствии атмосферы. При p — 0,75, — величина, близкая к той, которую дают наблюдения, при самой большой прозрачности воздуха, пунктирные кривые на фигуре 1 дают понятие о тех изменениях, который получатся в годовом ходе солнечной радиации под влиянием атмосферы.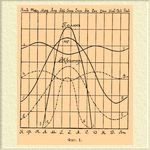
Фиг. 1.
Непосредственные измерения показывают, однако, что в действительности явление получается еще сложнее. В атмосфере имеется всегда некоторое количество водяных паров, сильно поглощающих солнечные лучи. Количество паров в данном объеме или данной массе воздуха есть величина переменная, зависящая от температуры и от степени насыщения воздуха. Поэтому предвычислить влияние паров на поглощение солнечной энергии в атмосфере очень затруднительно. Наблюдения Савельева в Киеве, Крова в Монпелье, Колли и Мышкина в Петровско-Разумовском, близ Москвы, значительно осветили влияние этого фактора на солнечную радиацию и показали, что только в ясные, безоблачные зимние дни, когда количество паров в атмосфере очень невелико, кривая суточного хода радиации приближается к своему теоретическому виду (кривая aa'a на фиг. 2. В летние дни на той же кривой около полудня появляется второстепенный минимум (кривая bb'b), благодаря тому, что с возрастанием температуры к полудню увеличивается, вследствие испарения, и количество паров в воздух; поглощение лучей атмосферой также растет с увеличением паров; вследствие этого кривая к полудню и падает.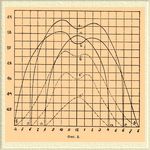
Фиг. 2.
Наибольшее количество энергии получается земной поверхностью в ясный весенний день (кривая сс'с); но и здесь уже второстепенный минимум около полудня ясно заметен. Нечто подобное получается и в годовом ходе радиации по непосредственным наблюдениям в Киеве. Кривая годового хода, быстро возрастая от зимы к весне и лету, достигает своего максимума не во время солнцестояния, а в мае месяце, после чего она обнаруживает слабый второстепенный минимум, зависящий от возрастания количества паров в воздухе. В сентябре наблюдается вторичный, более слабый максимум. Количество энергии, приносимой солнечными лучами на земную поверхность, сделалось предметом точных изменений только в последнее время, когда были выработаны методы для его изучения. При измерениях энергия солнечных лучей поглощается зачерненной поверхностью, покрытой обыкновенно сажей, и переводится вся таким образом в теплоту, которая и тратится на нагревание этой поверхности; это-то нагревание собственно и измеряется. Поверхность для полной определенности и сравнимости всех наблюдений ставится всегда перпендикулярно к падающим на нее лучам. Результаты измерения выражаются обыкновенно количеством малых калорий, поглощенных поверхностью в 1 кв. стм в течение 1 минуты. Основанные на этих началах приборы, известные под названием актинометров и пиргелиометров, были уже описаны в соответственных местах (см. соотв. статью). При актинометрических измерениях получается всегда интенсивность радиации на пластинку, поставленную нормально к падающему на нее лучу; поэтому непосредственные измерения дают в ясный, солнечный день величины, большие изображенных на фиг. 2 пунктиром; получаемые при непосредственных наблюдениях данные изображены на той же фиг. сплошными линиями. Для получения из этих чисел энергии, приходящейся на единицу горизонтальной земной поверхности, приходится результаты наблюдений умножить на синусы высот Солнца, что и дает пунктирные кривые. Производимые систематически или записываемые самими приборами автоматически наблюдения над С. радиацией дали возможность определить с достаточной вероятностью факторы, входящие в уравнение, выражающее закон Бугера. Для величины J, т. е. для интенсивности С. радиации на пределе атмосферы, называемой обыкновенно солнечной постоянной, наиболее вероятные значения, по наблюдениям Лэнглея, Крова и Савельева, колеблются между 3,0 и 3,5 калорий на см 2 в мин.; для p — коэффициента прозрачности атмосферы, значения колеблются между 0,8 и 0,5, в зависимости от различных обстоятельств, — главнейшим образом от содержания в воздухе паров и пыли. Здесь, конечно, разумеются ясные дни. При пасмурной погоде эти величины очень малы, об этом см. также — Лучистая теплота. Измерения при помощи актинометров и пиргелиометров достаточно сложны для обыкновенных метеорологических станций. Поэтому наблюдатели этих последних, для составления себе грубого представления о ходе С. радиации, пользуются гелиографами (см.). Этот прибор измеряет, собственно говоря, даже и не интенсивность С. радиации, а только продолжительность сияния Солнца в течение суток. Но даже и эти данные представляют значение для науки и жизни. Помимо того, что воздух сам поглощает лучи Солнца, плавающие в нем облака, становясь на пути лучей, заграждают им доступ к земной поверхности. Эти-то облака и записывает гелиограф. Зная по нему время, когда Солнце светило беспрепятственно на Землю, можно, хотя только с очень грубым приближением, составить себе понятие о С. радиации в течение суток.
Для ознакомления с современным состоянием вопроса о С. радиации — см. курсы Augot, "Trait é élémentaire de Mété orologie" (Пар., 1899); Лачинов, "Основы метеорологии и климатологии" (СПб. 1895).
Г. Любославский.
| "БРОКГАУЗ И ЕФРОН" >> "С" >> "СО" >> "СОЛ" >> "СОЛН" |
Статья про "Солнечная радиация" в словаре Брокгауза и Ефрона была прочитана 1771 раз
| Английское куриное карри |
| Английское куриное карри |
TOP 15
- Волос
- Проно
- Степные животные
- Гимнастика
- Индийский океан
- Архитектура
- Сравнение, в литературе
- Манда
- Клитры
- Колесование
- Испарение
- Травоядные животные
- Оплодотворение у pacтений
- Вредные насекомые
- Электризация тел