


БНБ
"БРОКГАУЗ И ЕФРОН" (121188)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Растворы
Определение "Растворы" в словаре Брокгауза и Ефрона
Растворы
Растворы*
Содержание: Понятие о Р. — Однородность Р. — Растворимость. Насыщение и пересыщение Р. — Замерзание Р. Криогидраты. — Упругость пара Р. — Удельные веca слабых Р. солей. — Осмотическое давление и физико-механическая теория Р. — Цвет водных Р. солей. — Химизм Р. Физико-химическая теория Р. — Образование Р.
Жидкости в природе всегда представляют растворы. "Ключевая", "речная", "морская", "метеорная" воды — все это Р. При исследованиях химических превращений тел, при разного рода химических операциях, применяемых в заводском деле и обыденной жизни, приходится также иметь дело по преимуществу с растворами. Их изучение представляет большой практический и теоретический интерес: здесь связующее звено между химией и физикой и главное содержание физико-химии. Образование Р. часто сопровождается внешними признаками химического соединения, причем, однако, процесс не связан с определенными, постоянными отношениями. Состав Р., количества тел, образующих Р., могут непрерывно варьировать — или беспредельно, или в определенных границах без нарушения однородности Р.; непрерывные изменения состава и свойств Р. открывают здесь широкое поле для применения физических методов исследования. Под именем Р. разумеют обыкновенно жидкие тела непрерывно-переменного состава, но в последнее время именем Р. стали называть и твердые тела, если они при видимой однородности представляют непрерывные изменения состава. К этой категории "твердых Р." относят сплавы, стекла, изоморфные смеси, явления акклюзии (см. это слово). Наконец, именем Р. газообразных предложено также называть смеси газов, так как в газовых смесях по мере увеличения их плотности и по мере приближения их к критической температуре наблюдаются значительные уклонения от простых законов для газовых смесей. Так, наблюдается, что количество вещества, которое может находиться в данном объеме в форме пара, различно, смотря по тому, находятся ли в том же пространстве другие газы и под каким давлением или нет. Напр., при испарении брома в пространство, наполненное сжатым до 300 атмосфер кислородом, количество брома в парах раз в 6 больше, чем при испарении в пустоту; увеличение плотности насыщенного пара брома ясно заметно уже при давлении кислорода в 5 атмосфер. Сжатый кислород "растворяет" бром. Болотный газ и этилен в газообразном состоянии, при значительном давлении подобным же образом "растворяют многие органические соединения не только низкокипящие, но и такие, как парафин, стеариновая кислота, камфора" (Вилляр). Сжатые газы, не превращаясь в жидкость, обнаруживают свойство жидкости — способность растворять тела. С другой стороны, взяв жидкий Р. и прибавляя все большие и большие количества одной из его составных частей, мы приводим другую в состояние разрежения, характерное для газа, т. е. получаем возможность осуществить в жидком состоянии как бы переход к газообразному состоянию. Если и на почве явлений растворения устанавливается связь между тремя состояниями тел, то все же в наиболее полной, типической форме представлены Р. в жидкой среде. Эти "жидкие Р.", за которыми установилось название Р., и составят предмет настоящей статьи.
Однородность Р. — Гей-Люссак показал, что однородность Р. не нарушается при продолжительном хранении Р. при постоянной температуре, хотя бы образующие Р. тела представляли значительную разницу в удельном весе. Позднее указывали (Бишоф), что при этом происходит нарушение однородности Р. так, что внизу раствор делается богаче той составной частью, которая имеет больший удельный вес. Но опыты Соре показали, что такое нарушение однородности Р. происходит лишь при неодинаковости температуры Р.: если поддерживать продолжительное время в верхних частях Р. солей более высокую температуру, чем в низших, то Р. делается неоднородным, в верхних частях количество соли уменьшается, а в нижних (холодных) увеличивается (см. Осмос). Теоретические соображения указывают необходимость нарушения однородности Р. под влиянием разницы в удельных весах составных частей и при отсутствии различия в температуре Р., но приводит к столь незначительным различиям в составе, какие при доступных опытной проверке условиях не могут быть обнаружены.
Растворимость. Насыщенные и пересыщенные Р. Весьма часто растворение прекращается, когда достигнута определенная величина "крепости", или концентрации, Р., т. е. определенное весовое количество растворяемого тела в единице объема или в единице веса Р., при которой дальнейшее растворение данного тела при данных условиях не происходит; такой Р. называется насыщенным. Насыщенные Р. представляют частный случай подвижного (химического) равновесия при неоднородности среды. Независимо от тех или иных представлений о природе Р. можно установить ряд общих положений относительно изменяемости величин растворимости — положений, применимых как для перемены физического состояния, так и для перемен, связанных с изменением химического состава, если эти перемены характеризуются обратимостью (см.). Насыщенный Р. представляет систему тел, способную испытывать обратимые перемены. Изменения температуры и давления вызывают непрерывные изменения крепости насыщенного Р., соприкасающегося с избытком растворяемого тела, а по восстановлении первоначальных температуры и давления крепость Р. тоже возвращается к первоначальной величине. Зависимость между температурой, давлением и растворимостью подчинена поэтому прежде всего правилу фаз (см.), согласно которому: если система при n компонентах представляет n +2 фаз (т. е. однородных частей), то все три величины, температура, давление и состояние веществ в фазах (в данном случае концентрации веществ в Р.), вполне определены (система нонвариантная); если n+1 фаз, то две величины вполне определены при определенной третьей; при n фаз одна вполне определена при определенном значении двух остальных и т. д. С помощью этого правила разбор вопросов растворимости упрощается. Необходимо при этом иметь в виду, что знание числа "компонентов" вовсе не требует никаких определенных предположений о состоянии тел внутри Р. Компоненты системы — это тела, способные переходить из фазы в фазу обратимым путем. Весь остаток за вычетом этих компонентов из состава данной фазы составляет один компонент, хотя бы это и был весьма сложный комплекс химических тел [Ненасыщенный водный Р. солей, напр., представляет систему двух фаз: жидкую (Р.) и пар. В этой системе два компонента: вода, способная переходить из одной фазы в другую обратимым путем, и весь комплекс солей, находящихся в Р. Как только Р. сделается насыщенным для одной из солей и она появится вне Р., прибавляется одна фаза и вместе с тем один компонент. В правиле фаз мы имеем дело с "компонентами системы", а не с компонентами Р. в том смысле, как мы говорим о компонентах газовой смеси. Немало имеется попыток для подобного же расчленения и Р. на компоненты, их слагающие, о чем будет речь далее. Правило фаз приводит к выводам, основанным прежде всего на данных относительно состояний тел вне Р., т. е. таких состояний, которые образуют отдельные фазы.]. Если Р. насыщен и сверх того имеется избыток растворяемого тела, то различают прежде всего три случая, смотря по тому, находится ли избыток растворяемого тела в газообразной, жидкой или твердой фазе. Этому соответствуют выражения: растворимость газов, жидкостей и твердых тел. Особенности явлений, при этом наблюдаемые, вовсе не указывают на необходимость допущения, что и внутри Р. тела сохраняют то состояние, в каком они соприкасаются с Р. При растворении газа в момент насыщения Р. мы имеем всего две фазы (жидкую и газообразную), т. е. мы имеем систему дивариантную, с числом фаз n (две фазы при двух компонентах): и температура и давление в такой системе могут изменяться независимо, и возможен ряд равновесий с непрерывно меняющимися температурами и непрерывно меняющимися давлениями. Чтобы установить величину растворимости, нужно относить ее всякий раз к условно избранным температуре и давлению. Принято считать растворимостью газа при данной температуре то его количество (выраженное объемом), которое растворяется при 760 мм давления в 1 или в 100 об. жидкости. Когда избыток растворяемого тела находится в жидкой или твердой фазе, тогда (предполагая, что опыт производится в пустоте) система представит n +1 фаз (при двух компонентах три фазы: твердую, жидкую и газообразную, или две жидких и газообразную). В такой системе и давление, и температура могут меняться только одновременно, и, чтобы определить состояние системы, нужно условно установить только одну из этих величин, ибо другая при этом неизбежно должна также иметь определенное значение. Отсюда особенности Р. твердых и жидких тел: величина растворимости может быть определена в зависимости только от температуры, и при данной температуре состав насыщенного Р. и давление его пара представляют определенные величины. Насыщенные Р. твердых и жидких тел при перегонке показывают постоянную температуру кипения (см. Кипение) до тех пор, пока имеются налицо все три фазы. Если из этой системы удалить одну из фаз, то степень подвижности системы увеличится на единицу и мы будем наблюдать те же соотношения, что и при растворах газов. Если, напр., исключить газообразную фазу и производить наблюдения так, чтобы пространство сосуда было сполна заполнено двумя фазами (жидкой и твердой, или двумя жидкими), то в таком случае растворимость будет зависеть не только от температуры, но и от давления. Эта зависимость подчинена общему для обратимых процессов закону: если растворение (превращение) связано с уменьшением объема, т. е. если объем Р. меньше суммы объемов до растворения (отнесенных к одному и тому же давлению), то увеличение давления увеличивает растворимость, и наоборот. Изменения объема при растворении твердых и жидких тел незначительны, а потому и изменения растворимости с давлением незначительны; но все же справедливость этого положения и в данном случае подтверждена прямыми опытами: при сжатии, напр., насыщенного при 20° Р. нашатыря давлением в 160 атмосфер наблюдается уменьшение содержания соли в Р. на 1%, a при сжатии насыщенных Р., напр. NaCl или CuSO 4 — наблюдается увеличение растворимости для NaCl на 1/250, a для CuSO 45H2 O на 1/33 при давлении в 100 атмосфер (Сорби); в первом случае — уменьшение объема при выделении тела из Р., во втором и третьем — наоборот. Если насыщение Р. происходит при участии двух фаз, из коих одна газообразная, то здесь растворение, переход из газообразной фазы в жидкую, неизбежно должно быть связано с громадным уменьшением или объема, или давления; поэтому растворимость газов чрезвычайно сильно увеличивается с увеличением давления. Для случаев сравнительно малой растворимости газов имеет место закон Генри-Дальтона: растворимость газа возрастает пропорционально его давлению, а при смеси газов растворимость каждого представляет ту же величину, какую он представил бы, если бы находился один под давлением, равным его парциальному давлению в смеси [Согласно этому закону, напр., воздух, растворенный в воде, должен иметь состав, близкий к отношению 2 об. азота на 1 об. кислорода, ибо растворимости азота и кислорода относятся друг к другу приблизительно как 1:2 (при 0°—2 и 4,1 объемов в 100 об. воды. при 20° — 1,4 и 2,8), а парциальные давления как 4:1, следовательно, объемы азота и кислорода, растворенные в воде, соприкасающейся с воздухом, будут относиться, как 4х1: 1х2 = 2:1]. Влияние температуры на величины растворимости определяется также общим для обратимых процессов законом: если растворение сопровождается поглощением тепла, то повышение температуры вызывает увеличение растворимости, и наоборот. Поглощение тепла наблюдается почти всегда при растворении твердых тел, ибо здесь растворение сопровождается переменой состояния, поглощающей тепло, а при растворении газов происходит выделение тепла. Растворимость газов уменьшается при нагревании, а растворимость твердых тел почти всегда увеличивается при нагревании [Образчиками различий в величинах растворимости твердых тел при разных температурах могут служить следующие примеры:
| Тело | Растворимость в 100 вес. частях воды при температурах | |||
| 0° | 25° | 50° | 100° | |
| NaCl | 35,52 | 36,13 | 86,96 | 39,61 |
| K2SO4 | 8,3 | 11,7 | 17,3 | 25,9 |
| KNO3 | 13,32 | 38,34 | 97,9 | 246,0 |
Формулу для выражения зависимости между растворимостью и температурой см. в ст. Химические равновесия.]. Р. жидкостей занимают среднее положение и представляют случаи и увеличения, и уменьшения растворимости при нагревании: иногда насыщенный Р. жидкостей мутится при нагревании, иногда при охлаждении. При достаточном повышении температуры растворимость жидкостей стремится к безграничной, т. е. смешение происходит, как в газах, при всех пропорциях. Это происходит, когда состав обеих жидких фаз сделается одинаковым: при неполной растворимости жидкостей оба тела находятся в двух жидких фазах, но в разном количественном отношении a/b и c/d; при повышении температуры a/b и c/d стремятся сделаться равными, и, когда этот момент наступает, различие между фазами исчезает, Р. делается однородным и растворимость делается безграничной. Наступление полной растворимости жидкостей аналогично появлению критического состояния в системах из жидкости и пара (О. Массон). Общие положения, выражающие зависимость между растворимостью, температурой и давлением, приложимы при наличности тех фаз и того их числа, к каким они относятся. Если из системы удалить одну из фаз, то в остающихся фазах изменения температуры и давления не вызывают непременно те же перемены, какие имели место при наличности удаленной фазы. Точно так же если одну из фаз заменить новой фазой тех же тел, то сохранение равновесия необязательно. Эти соображения должны быть прежде всего приняты во внимание при обсуждении вопроса пересыщенных Р. Если насыщенный нагретый Р. твердого тела — напр. соли — охладить с прибавкой избытка твердого тела, то по охлаждении часть этого тела выделится и в Р. останется такое его количество, какое соответствует растворимости тела при данной температуре. Но если охлаждение Р. производить без твердой фазы, то выделение твердого тела весьма часто не происходит и Р. по охлаждении остается "пересыщенным". Его состав неопределен и зависит от способа приготовления. В данном случае охлаждение применено к системе из двух фаз, и, как при явлениях растворимости газов, каждой температуре может отвечать целый ряд растворов разного состава. Только когда мы введем третью фазу, состав Р. должен выразиться определенной величиной при определенной температуре. Пересыщенный Р. неизбежно выделяет избыток соли, если мы введем весьма малое количество твердой фазы, т. е. крупинку готового кристалла соли. Твердые тела представляют многочисленные случаи полиморфизма, а также многочисленные формы соединений с водой. Если все такие видоизменения растворимы в воде, то все они при растворении будут представлять фазы данного тела. Кристалл каждой из этих разностей, будучи брошен в пересыщенный Р., вызовет выделение тела в той же фазе, т. е. в той же форме, какая уже соприкасается с раствором; наступит состояние равновесия, Р. становится насыщенным, причем растворимость при данной температуре представляет одну и ту же величину, если твердая фаза одна и та же, и разные величины при замене одной твердой фазы другой [Образчиками paзличий в величинах растворимости одного и того же тела при различии его фаз могут служить следующие данные для растворимости углекислого натрия:
| 0° | 10° | 20° | |
| Na2CO310H2O | 7,0 | 12,1 | 21,7 |
| Na2 СO 37H2 O (квадратн.) | 20,4 | 26,8 | 38,6 |
| Na2 СO 37H2 O (ромбоэдр.) | 81,3 | 37,9 | 45,8 |
Р., насыщенный в отношении последней фазы, будет сильно пересыщен в отношении двух первых; Р., насыщенный для второй фазы, будет пересыщен для первой и ненасыщен для третьей. Приготовляя Р. с помощью любой из этих фаз, мы получим одни и те же свойства Р. при одинаковой концентрации: различие в величинах растворимости зависит в данном случае от различия состояний вещества вне Р., а не внутри Р.]. При таких условиях одновременное образование из пересыщенного Р. двух твердых фаз невозможно, и если при кристаллизации опустить в Р. одновременно две разности, то та, которой отвечает большая растворимость, исчезает и тело кристаллизуется в разности, которой соответствует меньшая растворимость. Одновременное присутствие в Р. двух твердых фаз дает систему с n +2 фазами (при двух компонентах — четыре фазы: две твердые, жидкая и газообразная). Это система нонвариантая: все четыре фазы наблюдаются при определенных температуре и давлении. Ни нагревание, ни охлаждение не вызывают изменения температуры системы, а лишь исчезание одной из твердых фаз, и, когда одна из твердых фаз исчезнет, наблюдают обычные изменения Р. при одной твердой фазе. Такой случай представляет напр. нагретая до 33° глауберова соль Na 2SO4 10Н 2 O, образующая при этом Р., Na 2SO4 и водяной пар. Все эти четыре фазы могут быть наблюдаемы в одной системе только при 33°; охлаждением системы Na 2SO4 превращает при неизменной температуре в Na 2SO410H2 O, a нагреванием Na 2SO410H2 O в Na 2SO4 при той же температуре (подробности см. Правила фаз). Нонвариантные системы называются также "переходной точкой". В явлениях растворимости "переходная точка" обнаруживается резкой переменой в ходе растворимости, переломом кривой, выражающей зависимость растворимости от температуры, причем каждая из ветвей кривой отвечает особой фазе. Следствием этого может явиться максимум растворимости, если сопоставлять величины растворимости, соответствующие разным фазам. Примером могут служить растворимости глауберовой соли и хлора в воде. Выражением наблюдаемых здесь соотношений может служить прилагаемый схематический чертеж. Здесь максимум растворимости наблюдается потому, что ab отвечает растворимости твердых гидратов (Na 2SO410H2 O) и Сl 210H2 O), образующих Р. с поглощением тепла (восходящая кривая), а bс — отвечает растворимости хлора и Na 2SO4, образующих Р. с выделением тепла (падающая кривая).
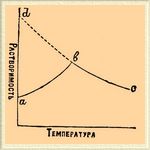
Обозначенная пунктиром ветвь bd соответствует растворам, пересыщенным для гидратов и насыщенным для безводных тел. Вне "переходной точки" при данной температуре столько величин растворимости, сколько фаз для данного тела. Кроме возможности появления тела в нескольких твердых фазах, необходимо принять во внимание и возможность появления тела в жидкой фазе в виде переохлажденной жидкости при температуре гораздо ниже температуры плавления тела. Выделение из Р. твердых тел при обыкновенной температуре в жидком состоянии наблюдается не только для таких легкоплавких тел, как фосфор и сера. Вызывая образование осадков солей под микроскопом, Линк убеждался, что мелкая муть в первый момент состоит из жидких капель, сливающихся друг с другом и затем принимающих кристаллическую форму. Выделению тела в жидкой фазе соответствует образование пересыщенных Р., весьма неустойчивых, в которых кристаллизация происходит или сама собой, или от трения о стенки сосуда, или толчка. Если же тело образует несколько твердых фаз, то пересыщенные его Р. часто представляют такую устойчивость, что без прикосновения с готовым кристаллом тела [Или тела, с ним изоморфного. Кристаллизация пересыщенных Р. от соприкосновения с воздухом обусловливается присутствием в воздухе кристаллической пыли.] сохраняются неопределенное время. При разложении Р. на жидкие фазы явления пересыщения не наблюдаются. На этом основан простой метод определения растворимости жидкости (Алексеева), основанный на наблюдениях температуры появления мути в Р. жидкостей известного состава. Определение растворимости твердых тел сложнее, требует тщательного перемешивания Р. с исследуемой твердой фазой, отделения Р. при той же температуре и затем анализа Р. В газах явления пересыщения происходят также при отсутствии газообразной фазы, т. е. отсутствии свободной поверхности, оттого Р. газа выделяет его при медленном нагревании в виде пузырьков на поверхности сосуда, при чем в массе жидкости Р. остается долгое время пересыщенным, утрачивая это состояние медленно, путем диффузии к поверхности. Встряхивание Р. или всыпание какого-либо порошка вызывает в таком пресыщенном P. газа явление, подобное кипению. Определения растворимости газов производятся большей частью наблюдением изменений объема и давления газа, помещенного в одном колене манометра, после прикосновения газа с данной жидкостью. Численные данные для величин растворимости см. Таблицы коэффициентов.
Замерзание Р. Криогидраты. Если водный Р. охладить ниже 0° и бросить кристалл льда, то при достаточном охлаждении Р. выделит новые количества льда, наступит равновесие, причем Р. будет насыщен в отношении твердой фазы одного из компонентов Р., именно воды. Такие явления кристаллизации из Р. при температурах, близких к температуре замерзания данного тела в чистом виде, называются замерзанием Р. и представляют частный случай образования из Р. твердых фаз, определяющих величину растворимости. Здесь также наблюдается переохлаждение, т. е. пересыщение Р.: не раствор замерзает, а из него "вымерзает" один из компонентов в чистом виде [Оба компонента содержатся непременно в твердой фазе, если тела изоморфны или вообще если они способам образовать "твердый Р."]. Особенное название для этого явления сохраняется потому, что цель таких наблюдений — сравнение температуры кристаллизации из Р. с температурой замерзания данного тела в чистом виде. Температура кристаллизации тела из Р. всегда ниже температуры замерзания тела в чистом виде; разность этих температур назыв. депрессией, или понижением температуры замерзания. Величины депрессии темп. замерзания служат основанием для важных выводов, в особенности в приложении к слабым Р. В таких Р., согласно закону Благдена, величина депрессии пропорциональна крепости Р., т. е. пропорциональна концентрации находящегося в Р. тела: депрессия, производимая единицей веса, или специфическая депрессия, представляет, следовательно, в слабых Р. постоянную величину, не зависящую от концентрации Р. и характерную для растворенного тела. Исследования Рауля показали, что при одном и том же растворителе специфические депрессии для ряда тел представляют величины, обратно пропорциональные частичному весу этих тел, или депрессии, производимые количествами тел, пропорциональными их частичным весам, так наз. молекулярные депрессии темп. замерзания, представляют величины постоянные. Закон Рауля имеет место также для слабых Р. Молекулярная депрессия получается делением величины депрессии для Р. данной крепости на величину концентрации и умножением на молекулярный вес. Некоторые тела показывают величины молекулярной депрессии аномальные, большие или меньшие, чем нормальная молекулярная дeпрессия, наблюдаемая для ряда тела. Эти аномалии объясняются образованием более сложных частиц или диссоциаций. Нормальные молекулярные депрессии D = md/p представляют, напр., для нижепоименованных растворителей след. (средние) величины: вода — 18,5, бензол — 49, уксусная кислота — 39, бромистый этилен — 117. Здесь m — молекулярный вес растворенного тела, d — депрессия, производимая при растворении p весовых частей тела в 100 част. растворителя. Величины нормальных молекулярных депрессий тем больше, чем больше молекулярный вес растворителя. Точной пропорциональности здесь нет; особенно выделяется вода; молекулярная депрессия в водных Р. гораздо больше, чем можно было бы ждать по величине молекулярного веса воды, что принимается за указание большей сложности частиц воды в жидком состоянии, чем у других жидкостей (см. ассоциация в статье Жидкости). При замерзании крепких Р. особый интерес представляют те случаи, когда обе составные части Р. кристаллизуются одновременно и Р. замерзает целиком. Если такое полное замерзание Р. не сопровождается изменением его состава, то полученная твердая масса называется криогидратом (см.). Криогидрат образуется из Р. определенного состава, расплавляется и замерзает нацело при постоянной температуре. Эти свойства криогидратов характерны и для химических соединений определенного состава, и для нонвариантных систем с числом фаз равным n+2. Криогидраты отвечают этому последнему условию, так как их состав не выражается простыми частичными формулами. Нонвариантной система будет в данном случае, если криогидрат представляет смесь двух твердых фаз (льда и соли) и при плавлении или замерзании криогидрата будет при двух компонентах четыре фазы: пар, раствор и две твердых фазы. Это определение не решает, однако, вопроса о состоянии тел в твердой фазе: криогидрат будет представлять две твердых фазы и в том случае, если, напр., почти вся масса воды будет образовывать соединение с солью определенного состава и в твердой массе будет заключаться лишь незначительное количество льда.
Упругость пара Р. представляет наиболее простые соотношения в том случае, когда в пар переходит одна из составных частей раствора. Система представляет те же особенности, что и Р. газа. Как и при замерзании Р., исследование направлено и здесь на изучение депрессий, именно разностей между упругостью пара чистого растворителя и упругостью пара Р. Упругость пара Р. меньше, температура кипения выше, чем для чистого растворителя (см. Кипение). Депрессии упругости пара обнаруживают в слабых Р. законности, аналогичные тем, которые указаны при замерзании Р.: при данном растворителе и данной температуре депрессии упр. пара пропорциональны концентрации (Вюльнер) и обратно пропорциональны молекулярному весу растворенного тела (Рауль). Эти величины с температурой возрастают, согласно Бабо, так, что отношение (p—p1)/p остается постоянным (здесь p и p1 — упругости пара растворителя и Р.). Необходимость связи между депрессией темп. замерзания и депрессией упругости пара указана теоретически Гульдбергом и Колачевским на основании положения: при температуре замерзания упругость пара, выделяемого льдом (или вообще твердой фазой), и жидкостью, в которой лед находится, должны быть равны. Пользуясь данными механич. теории тепла и предполагая законы Вюльнера и Бабо справедливыми, т. е. предполагая, что (p—p1)/p = α C, где С — концентрация Р., а α — постоянная величина, получим формулу для водных растворов: d = 105 α C, где d — депрессия температуры замерзания. Формула приближенная; она наглядно показывает связь между обеими депрессиями. Величины молекулярных депрессий упругости пара, т. е. величины [ (p—p1)/ С ]M, где M молекулярный вес растворенного тела, можно освободить от влияния температуры, пользуясь законом Бабо: (p—p1)/p = const. Тогда, как показал Рауль, получается для слабых Р. весьма простое выражение: (p—p1)/p
n/N, где n — число частиц растворенного тела, N — число частиц растворителя, т. е. если составить раствор в такой напр. пропорции, чтобы на 100 частиц растворителя приходилась бы 1 част. растворенного нелетучего тела, то упругость пара Р. будет на 1% меньше упругости пара чистого растворителя. Этот закон, так же как и соответствующий закон замерзания Р., может служить для определения молекулярного веса тел, пользуясь растворением, взамен испарения тел (см. Газы). Кроме небольших отступлений, приписываемых приближенности закона, здесь также наблюдаются аномальные величины молекулярных депрессий, служащие основанием для таких же предположений, какие указаны при замерзании Р. [Об упругостях пара Р. при летучести обоих составных частей см. Кипение.].
Удельные веса слабых водных Р. солей подчинены, согласно наблюдениям Вальсона, простому закону, именно правилу модулей, т. е. правилу постоянных разностей. Если сравнивать Р. различных солей при содержании эквивалента соли (в граммах) в литре Р., то оказывается, что разность уд. веса для солей разных кислот будет одна и та же, каков бы ни был металл соли, а для солей разных металлов — одна и та же, какова бы ни была кислота. Таким образом, уд. вес Р. соли может быть вычислен, прибавляя к уд. весу какого-нибудь условно выбранного Р. (Вальсон брал уд. вес Р. нашатыря) 2 постоянные величины разностей (модулей). Увеличение уд. веса воды от растворения в ней соли может быть, таким образом, представлено суммой двух величин, одной — постоянной для данного металла, другой — постоянной для данной кислоты. Тот же способ выражения суммой двух величин предложен Кольраушем для электропроводности (или гальванопроводности) солей в слабых Р. Возможность вычисления величины молекулярной электропроводности при бесконечном разведении сложением величин "подвижностей" ионов служит одним из главных аргументов в пользу физико-механической теории Р. (см. Гальванопроводность).
Осмотическое давление и физико-механическая теория Р. Для слабых Р. уже указан ряд правильностей, аналогичных законам газообразного состояния. Одинакова не только форма зависимости свойств от концентрации как в газах, так и в слабых Р.: но кроме того, и влияние природы растворенного вещества здесь по отношению к депрессиям температур замерзания и упругости пара может быть сведено к величине молекулярного веса, как это имеет место по отношению к плотностям газов. Эта аналогия между состоянием веществ в слабых Р. и в газообразном состоянии доведена до высокой степени наглядности путем анализа величины осмотического давления (см. Осмос). Когда Р. заключен в оболочку, проницаемую только для растворителя, и погружен в растворитель, то состояние равновесия наблюдается только в том случае, когда Р. сжат и когда величина производимого на оболочку "осмотического давления" представляет определенную величину; в противном случае крепость Р. или уменьшается, или увеличивается от проницания растворителя к Р. или из Р. Величина этого давления, как показали расчеты Вант-Гоффа, близка к величине газового давления, т. е. к величине давления, которое обнаруживало бы растворенное вещество, если бы оно в том же количестве и в том же объеме находилось в состоянии газа (см. Осмос). Отношение этих величин обозначается через i. Вант-Гофф показал, что i близко к единице, когда растворенное тело обнаруживает нормальные величины "депрессий". Необходимость такого соотношения может быть наглядно показана следующим образом (Аррениус). На фиг. А — сосуд с полупроницаемым (проницаемым только для растворителя) дном b, наполненный раствором, В — сосуд с растворителем.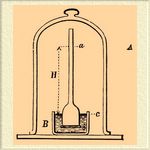
Растворенное тело нелетуче, и пространство, в котором находится прибор, наполнено парами растворителя. Требуется определить, какая разница уровней H отвечает состоянию равновесия. В этом состоянии ни через дно b не будет движения растворителя путем осмоса, ни на поверхноcти а — путем испарения. В самом деле, выбрав надлежащий столб Р. H, мы уравновесим осмос, и если при этом мы не уравновесили бы испарения, то получился бы род perpetuum mobile — постоянное движение пара от одного сосуда к другому. Давление пара на поверхности с больше, чем на поверхности b, на величину веса столба пара высотою H. Этот вес дает меру депрессии упругости пара на поверхности Р. (а). С другой стороны, высота H определяет вес столба Р., уравновешивающего осмотическое давление. Предполагая известной величину осмотического давления, можно, следовательно, вычислить депрессию упругости пара и наоборот. Предполагая, что взят Р. столь слабый, что удельный вес его можно принять равным удельному весу растворителя, что пар обладает при данной упругости нормальной плотностью, т. е. соответствующей моллекулярному весу растворителя, и произведя соответствующие расчеты, получим, что при нормальном осмотическом давлении, т. е. при i = 1, депрессия упругости пара будет представлять нормальную величину соответственно закону Рауля: (p—p1)/p = n/N. Если i <> 1= k, то и (p—p1)/p = k(n/N). Раньше была указана возможность вывода отношения между депрессиями замерзания и упругости пара с помощью механической теории тепла. Этот вывод требует знания скрытой теплоты плавления растворителя. Пользуясь приемом осмотического давления и законами термодинамики, Вант-Гофф нашел зависимость между величиной молекулярной депрессии температуры замерзания, скрытой теплотой плавления растворителя и величиной i. Если i = 1,, то молекулярная депрессия темп. зам. D = 0,02(T2 /W), где W — скрытая теплота плавления, а T — температура плавления растворителя в абсолютных градусах. Напр., для воды W = 79, Т = 273, следовательно, D = 18,9, а по Раулю нормальная молекулярная депрессия температуры замерзания водных Р. — 18,5. Такое же согласие найдено и для других растворителей. Зная скрытую теплоту замерзания растворителя, мы можем, следовательно, заранее вычислить нормальную величину молекулярной депрессии температуры замерзания. Такая величина, вместе с тем, соответствует нормальной величине осмотического давления, т. е. i = 1. Эти выводы основаны на законах механической теории тепла и теории Р. не заключают. Возникшая на почве этих соотношений физико-механическая теория Р. начинается со следующих положений: 1) состояние вещества в разбавленном Р. вполне аналогично состоянию газа; 2) в нормальных случаях молекула растворенного вещества в разбавленном Р. одинакова с молекулой того же вещества в газообразном состоянии; 3) "аномалии" при достаточном разведении Р. происходят исключительно или от увеличения, или от уменьшения числа молекул растворимого тела, т. е. или от диссоциации растворенного тела, или от соединения его молекул в более крупные агрегаты. Особенно важное место в этой теории принадлежит истолкованию явлений электропроводности растворов. Аномально большие величины i наблюдаются иногда в таких случаях, когда предположить явления обычной диссоциации невозможно. Так, для растворов НСl i близко к двум, между тем никаких признаков свободного хлора и водорода, притом в состоянии свободных атомов, Р. не обнаруживает [Такая же величина i наблюдается, напр., и для КСl, но там аномалию можно объяснять увеличением числа частиц путем гидрализа: КСl + Н 2 О = КНO + НСl]. Такие аномалии привели к предположению о существовании особой диссоциации — электролитической, результатом которой являю
| "БРОКГАУЗ И ЕФРОН" >> "Р" >> "РА" >> "РАС" >> "РАСТ" |
Статья про "Растворы" в словаре Брокгауза и Ефрона была прочитана 2187 раз
| Салат с Кальмарами |
| Луковый соус |
TOP 15
- Волос
- Проно
- Степные животные
- Гимнастика
- Индийский океан
- Архитектура
- Сравнение, в литературе
- Манда
- Клитры
- Колесование
- Испарение
- Травоядные животные
- Оплодотворение у pacтений
- Вредные насекомые
- Электризация тел