


БНБ
"БРОКГАУЗ И ЕФРОН" (121188)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Правильная система
Определение "Правильная система" в словаре Брокгауза и Ефрона
Правильная система
Правильная система*
(кубическая, тессеральная) — обнимает собой совокупность кристаллов, в которой имеются три единственных в своем роде взаимно перпендикулярных между собой равных направления, проходящих через центр кристалла. Эти три линии соединяют три пары взаимно противоположных одинаковых элементов огранения, которые находятся в кристалле только в количестве трех пар. Указанные направления являются в то же время осями симметрии 4-го или 2-го порядков (смотря по степени симметрии). Совместив с ними координатные оси и приняв их отрезки, внутри простых форм лежащие, за кристаллические оси, можно сказать, что П. система характеризуется тремя равными взаимно-перпендикулярными кристаллическими осями. У всех у них имеется четыре оси симметрии 3-го порядка. Кроме общих черт гоометрического характера, кристаллы П. системы обладают еще и многими другими сходными признаками; так, они являются изотропными в оптическом отношении (за немногими исключениями, как это будет указано ниже), в отношении теплопроводности и электропроводности и нек. др. Кристаллы П. системы являются весьма распространенными как среди минералов, так и искусственных соединений. Большей частью это суть вещества в химическом отношении весьма простые: почти все элементы металлического характера — золото, серебро, платина, железо, медь, ртуть и др., также углерод в виде алмаза. Далее галоидные соединения, напр., хлористый натрий (каменная соль, поваренная соль), хлористый калий (сильвин), хлористое серебро; бромистый и йодистый калий и натрий; фтористый кальций (плавик); некоторые окислы, напр., закись меди (куприт); особенно много в этой системе кристаллизуется сернистых соединений; из минералов укажем: серебряный блеск (Аg 2 S), свинцовый блеск (PbS), цинковая обманка (ZnS), серный колчедан (пирит), кобальтовый блеск (CoASS), никелевый блеск (NiSbS), блеклые руды и др. В этой же системе кристаллизуется обширная группа шпинелей, состав которых может быть представлен RO.R 2O3. Среди силикатов П. система пользуется меньшим распространением: сюда относятся, напр., гранаты. Степень симметрии у кристаллов П. системы различна: они отличаются друг от друга числом плоскостей симметрии, числом и характером осей симметрии, присутствием или отсутствием центра симметрии. В этом отношении они легко разбиваются на пять групп, называемых также классами, для которых существуют различные названия. В настоящее время классы называют именем простой формы, грани которой делают различные отрезки по координатным осям.
I-й класс, обладающий наибольшей степенью симметрии не только среди кристаллов П. системы, но и всех других систем, называется классом сорокавосьмигранника (гексакис-октаэдра). В кристаллах, сюда относящихся, имеются: центр симметрии (С), три оси симметрии 4-го порядка (3L 4), четыре оси 3-го порядка (4L 3), шесть осей 2-го порядка (6L 2) и девять плоскостей симметрии (9Р), из которых три равнозначных проходят через оси симметрии 4-го порядков. Простые формы (т. е. кристаллы, ограниченные одинаковыми в геометрическом и в физическом отношениях плоскостями), возможные для данной степени симметрии, имеют следующий вид и наименования: 1) сорокавосьмигранник (иксагис-октаэдр) общий представитель всего класса; его символ (обозначение) [hkl]. На фиг. 1 изображен сорокавосьмигранник символа [632]. 2) Икоситетраэдр, или трапецоэдр; символ [hkk]. Фиг. 2 изображает трапецоэдр, символ которого [211].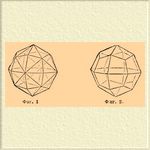
Фиг. 1. Фиг. 2.
3) Пирамидальный октаэдр (триакис-октаэдр); символ [hhl]; изображен на фиг. 3; символ [221]. 4) Пирамидальный куб (тетракис-гексаэдр); символ [hko]; изображен на фиг. 4.
Фиг. 3. Фиг. 4.
5) Куб (гексаэдр, фиг. 5); символ [100]. 6) Октаэдр (фиг. 6); символ [111].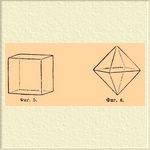
Фиг. 5. Фиг. 6.
7) Ромбический додекаэдр (гранатоэдр; фиг. 7); символ (110). Указанные формы обыкновенно встречаются в комбинациях друг с другом; например фиг. 8 изображает комбинацию октаэдра с ромбическим додекаэдром. В этом классе кристаллизуются, например, квасцы, плавиковый шпат, гранаты, шпинели и др.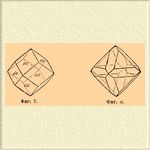
Фиг. 7. Фиг. 8.
II. Второй класс характеризуется присутствием только осей симметрии, таких же и в том же количестве, как и в предыдущем классе: 3L 4, 4L3, 6L2. Он называется классом гироэдра, или пентагонального икоситетраэдра, который и служит представителем. Возможны два гироэдра, с одними и теми же индексами в символе и с гранями одинакового вида и размеров, но расположенными таким образом, что эти гироэдры не могут друг с другом совместиться; они являются зеркальным изображением один другого, подобно правой и левой руке, правому и левому глазу. Таким формам дают название эпаншиоморфных, и различают правый (фиг. 9) и левый гироэдр (фиг. 10); для первого символ [khl], а для второго — [hkl].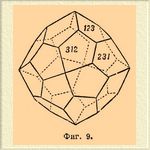
Фиг. 9.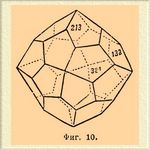
Фиг. 10.
Кроме гироэдра к этому же классу относятся еще шесть простых форм, которые по наружному виду ничем не отличаются от таких же форм первого класса (2, 3, 4, 5, 6 и 7). Их настоящая действительная симметрия обнаруживается только при изучении внутреннего строения, для чего наичаще пользуются так называемыми фигурами вытравления. В настоящее время заведомо известно только одно вещество, кристаллы которого принадлежат данному классу — это нашатырь или сальмиак (NH 4Cl).
III. Класс преломленного пентагонального додекаэдра (диакис-додекаэдра). Величина симметрии С, 3L 2, 4L3, 3Р. Сюда принадлежат: 1) преломленный пентагоналный додекаэдр — представитель класса символ [hkl] (фиг. 11); 2) Пентагональный додекаэдр; символ [hko] (фиг. 12).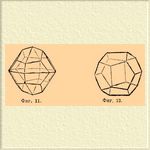
Фиг. 11. Фиг. 12.
Сверх того, сюда относятся формы по наружному виду тожественные с 2, 3, 5,6 и 7 первого класса, но отличающиеся своей внутренней симметрией, которая может быть обнаружена вытравлением. К этому классу принадлежат: серный колчедан, кобальтовый блеск и другие колчеданы.
IV. Класс преломленного пирамидального тетраэдра (иксакис-тетраэдра). Величина симметрии 3L 2, 4L3, 6Р. Представитель класса: 1) преломленный пирамидальный тетраэдр (фиг. 13); символ [khl]. К этому же классу принадлежат 2) пирамидальный тетраэдр (триакис-тетраэдр; фиг. 14); символ [hkk]; 3) дельтоэдр, (дельтоидный додекаэдр; фиг. 15); символ [hhl]; 4) тетраэдр (фиг. 16); символ [111].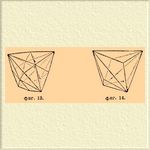
Фиг. 13. Фиг. 14.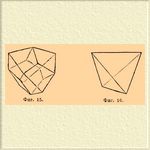
Фиг. 15. Фиг. 16.
В этом же классе встречаются: куб, пирамидальный куб и ромбический додекаэдр, отличающиеся от таковых же других классов своей внутренней симметрией. Характерной особенностью этого класса является полярность осей симметрии 3-го порядка — противоположные концы их не равнозначны, что особенно видно на пироэлектрических явлениях, которые наблюдаются в этом классе: один конец указанных направлений электризуется положительно, другой отрицательно (см. Пироэлектричество). У тетраэдра, пирамидального тетраэдра, дельтоэдра и преломленного пирамидального тетраэдра оси симметрии 3-го порядка, являются полярными и в геометрическом отношении: концы их соединяют неодинаковые точки; у тетраэдра, напр., один конец такой оси упирается в вершину трехгранного угла, а другой в середину грани кристалла. Для этого класса известны: блеклые руды, цинковая обманка, алмаз и др.
V-й класс, с наименьшей степенью симметрии в П. системе, называется классом тетартоэдра (тетраэдрического пентагонального додекаэдра). Степень симметрии выражается присутствием: 8L 2 и 4L 3. Представитель — тетартоэдр, подобно гироэдру, может быть правый (фиг. 17), в таком случае его символ [khl], и левый (фиг. 18) — символ его [bkl].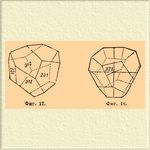
Фиг. 17. Фиг. 18.
Кроме тетартоэдра к этому классу принадлежат и другие формы, как-то: пентагональный додекаэдр, дельтоэдр, пирамидальный тетраэдр, тетраэдр, куб и ромбический додекаэдр, которые отличаются от таких же форм других классов симметрией внутреннего строения. Подобно предыдущему классу, оси симметрии 3-го порядка отличаются здесь полярностью. Сверх сего характерной особенностью данного класса служит отношение к поляризованному свету: некоторые кристаллы, сюда относящиеся, действуют на поляризованный свет, вращая плоскость его поляризации, причем те кристаллы, у которых находятся правые (в геометрическом смысле) формы, вращают плоскость поляризации вправо, а у которых левые — влево. Лучшим примером в этом отношении является хлорноватокислый натрий N aClO3, дающий правые и левые кристаллы (подробности см. в описании этой соли). Кроме названной соли к этому же классу принадлежат азотнокислые соли бария, стронция, свинца Ba(NO3)2, Sr(NO3)2, Pb(NO3)2 и нек. другие.
П. З.
| "БРОКГАУЗ И ЕФРОН" >> "П" >> "ПР" >> "ПРА" >> "ПРАВ" |
Статья про "Правильная система" в словаре Брокгауза и Ефрона была прочитана 1180 раз
| Пицца в сковороде |
| Салат тофу |
TOP 15
- Волос
- Проно
- Степные животные
- Гимнастика
- Индийский океан
- Архитектура
- Сравнение, в литературе
- Манда
- Клитры
- Колесование
- Испарение
- Травоядные животные
- Оплодотворение у pacтений
- Вредные насекомые
- Электризация тел