


БНБ
"БРОКГАУЗ И ЕФРОН" (121188)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Пар физ.-хим.
Определение "Пар физ.-хим." в словаре Брокгауза и Ефрона
Пар физ.-хим.
Пар (физ.-хим.)*
— Обыкновенно под словом П. понимают лишь газообразное состояние тела при температурах ниже критической, называя это состояние при температурах выше критической — газом этого тела. Парообразование совершается с поверхности не только жидких, но и твердых тел; так, напр., снег и лед сильно испаряются даже при весьма низких температурах; существует даже целый ряд тел (камфара, нашатырь), которые всецело переходят в П. — возгоняются, совершенно не переходя из твердого состояния в жидкое (объяснение этого явления см. Испарение). Обыкновенно же парообразование, незаметное в твердом теле, усиливается при переходе тела в жидкое состояние и в последнем сильно возрастает при повышении температуры. Механизм этого явления см. Испарение; там же см. Явления, сопровождающие испарение. При некоторой определенной температуре — темп. кипения (см.), зависящей от внешнего давления на тело, парообразование начинается во всей массе тела и при достаточном притоке тепла извне к телу продолжается до тех пор, пока все тело не перейдет в П. Увеличивая внешнее давление, можно повышать температуру кипения, но лишь до определенного предела — критической температуры (см.), выше которой тело при всяком давлении может существовать лишь в газообразном виде. Если поместить вещество в замкнутом пространстве при постоянной температуре, то образующийся из него П. будет мало-помалу заполнять пространство и, представляя газообразное тело, будет производить определенное давление на стенки сосуда и на вещество; это давление будет, согласно закону Дальтона, прилагаться к тому давлению, которое производят уже находящиеся в названной замкнутой оболочке другие газы, напр. воздух. По мере увеличения количества выделившегося П будет расти и производимое им давление, а следовательно, и его упругость, но лишь до известного предела, после которого дальнейшее выделение П. прекращается (но не парообразование, см. Испарение). Опыты показали, что при данной температуре выделение П. прекращается, независимо от сосуда и других наполняющих его газов, тогда, когда упругость П. достигла определенной величины, которую называют упругостью П. данного вещества, насыщающего пространство при данной температуре, или, сокращенно, упругостью насыщенного П. данного вещества при данной температуре. Разные вещества при одной и той же температуре имеют различнейшие упругости П., насыщающего и пространство, как видно из следующей таблицы:
Упругость паров, насыщающих пространство (в миллиметрах ртутного столбца), для температуры 20°С
| Ртуть | 0,0013 |
| Вода | 17,36 |
| Алкоголь | ,0 |
| Хлороформ | 160,5 |
| Сернистый углерод | 198,5 |
| Эфир | 442,4 |
| Сернистая кислота (SO 2) жидкая | 2162 (3,24 атм.) |
| Хлор жидкий | 5798 (7,63 ") |
| Аммиак жидкий | 6384 (8,4 ") |
| Углекислота жидкая | 44688 (58,8 ") |
От упругости П. зависит "летучесть" данного вещества при данной температуре и скорость его испарения. Зависимость упругости П. от температуры у разных тел различная, но у всех упругость растет с температурой, как видно, напр., из следующей таблицы:
Изменение упругости нас. П. с температурой (упругости даны в миллиметрах ртутного столба).
I — Серный эфир, II — аммиак жидкий в атм.
| Темп. | Ртуть | Вода | I | II |
| 0 | 0,00019 | 4,569 | 184,9 | 4,19 |
| 25 | 0,0020 | 23,517 | 361,0 | 9,84 |
| 50 | 0,013 | 91,978 | 1276,0 | 19,95 |
| 75 | 0,071 | 288,764 | 2991 (80°C) | 36,35 |
| 100 | 0,285 | 760,000 | 4859 | 61,32 |
| 125 | 1,10 | 1743,88 | 7495 (120°C) | — |
| 150 | 2,93 | 3581,23 | 13281 | — |
Особенный интерес представляет упругость насыщенных П. воды, так как содержание П. воды определяет степень влажности (см.) окружающего воздуха, и так как эти П. применяются в паровых машинах. Вопрос о зависимости упругости П. воды от температуры изучен был в особенности Магнусом (1844) и Реньо (1843) и привел к результатам (по Реньо), помещенным в таблице в ст. Вода.
Кирхгоф показал в 1858 г. теоретически, что при температуре перехода тела из твердого состояния в жидкое, упругость П. твердого тела и жидкого должна быть одинаковой; так, напр., при 0° упругость П. воды и льда равны 4,60 мм. Позже (1882) Герц указал на то, что у переохлажденной жидкости (т. е. у жидкости, искусственно охлажденной ниже ее температуры замерзания) упругость П. всегда должна быть больше, чем у твердого тела (застывшей жидкости) при той же температуре; это было вполне подтверждено опытами Рамзая и Юнга (1887), Фишера (1886) и Юдина (1893) над упругостью П. воды и льда. Так, напр., при 10° упругость П. переохлажденной воды (по Юлину) = 2,191 мм, а льда = 1,997 мм.
Некоторые соображения и опыты дают возможность предполагать, что и у твердых тел существует упругость П., насыщающих пространство, растущая с температурой. Этот вопрос, однако, еще весьма мало разработан; определенные данные существуют лишь для камфары (Рамзай и Юнг, 1887).
Упругость паров камфары (по Рамзаю и Юнгу) в мм ртутного столба.
| Темп. | Упругость |
| 41° 2 | 1,7 |
| 48,9 | 7,2 |
| 92,4 | 15,4 |
| 101,0 | 27,2 |
| 109,4 | 35,0 |
| 127,4 | 66,3 |
| 136,3 | 92,8 |
| 140, 3 | 105,0 |
| 147,0 | 155,1 |
| 154,3 | 197,6 |
| 168,0 | 297,8 |
Температура кипения жидкости — та температура, при которой упругость П. ее, насыщающего пространство, равна внешнему давлению (см. Кипение). Отсюда мы заключаем, что темп. кипения зависит от внешнего давления [О влиянии нa температуру кипения стенок сосуда — см. Кипение.] и что, напр., вода кипит при 100° лишь при давлении барометра в 760 мм, так как при 100° упругость П. ее равна 760 мм. Температура кипения воды при различных давлениях между 700 и 800 мм, а следовательно, и упругость П. воды при этих температурах даны в следующей таблице.
Температура кипения воды при давлениях от 700 до 800 мм рт. столба.
| Давл. | Темп. | Давл. | Темп. | Давл. | Темп. | Давл. | Темп. |
| 700 | 97,72 | 701 | 76 | 702 | 80 | 703 | 84 |
| 704 | 88 | 705 | 92 | 706 | 96 | 707 | 99 |
| 708 | 98,03 | 709 | 07 | 710 | 11 | 711 | 15 |
| 712 | 19 | 713 | 23 | 714 | 27 | 715 | 31 |
| 716 | 34 | 717 | 38 | 718 | 42 | 719 | 46 |
| 720 | 50 | 721 | 54 | 722 | 57 | 723 | 61 |
| 724 | 65 | 725 | 69 | 726 | 98,73 | 727 | 77 |
| 728 | 80 | 729 | 84 | 730 | 88 | 731 | 92 |
| 732 | 96 | 733 | 99 | 734 | 99,03 | 735 | 07 |
| 736 | 11 | 737 | 14 | 738 | 18 | 739 | 22 |
| 740 | 26 | 741 | 30 | 742 | 33 | 743 | 37 |
| 744 | 41 | 745 | 44 | 746 | 48 | 747 | 52 |
| 748 | 56 | 749 | 59 | 750 | 63 | 751 | 67 |
| 752 | 99,73 | 753 | 74 | 754 | 78 | 755 | 82 |
| 756 | 85 | 757 | 89 | 758 | 93 | 759 | 96 |
| 760 | 100,00 | 761 | 04 | 762 | 07 | 763 | 11 |
| 764 | 15 | 765 | 18 | 766 | 22 | 767 | 26 |
| 768 | 29 | 769 | 33 | 770 | 36 | 771 | 40 |
| 772 | 44 | 773 | 47 | 774 | 51 | 775 | 55 |
| 776 | 58 | 777 | 62 | 778 | 100,65 | 779 | 69 |
| 780 | 73 | 781 | 76 | 782 | 80 | 783 | 83 |
| 784 | 87 | 785 | 90 | 786 | 94 | 787 | 98 |
| 788 | 101,01 | 789 | 05 | 790 | 08 | 791 | 12 |
| 792 | 15 | 793 | 19 | 794 | 22 | 795 | 26 |
| 796 | 30 | 797 | 33 | 798 | 37 | 799 | 40 |
| 800 | 44 | 801 | 47 | 802 | 50 | 803 | 53 |
Нижеследующая таблица дает температуры кипения при давлении барометра в 760 мм для некоторых веществ.
Температуры кипения.
| Эфир | 84,9°C |
| Сернистый углерод | 46,2° |
| Алкоголь | 78,4° |
| Бензол | 80,4° |
| Вода | 100° |
| Тол | 175° |
| Анилин | 184° |
| Фосфор | 213° |
| Ртуть | 357° |
| Сера | 447,5° |
| Цинк | 930° |
Под весьма сильными давлениями можно нагреть жидкость значительно выше ее нормальной температуры кипения; напр., под давлением в 10 атмосфер вода закипает лишь при температуре в 180°, а под давлением в 20 атмосфер лишь при 215°. По причине этого вода в паровых котлах обыкновенно перегрета выше 100°; на этом же основано устройство Цапинового котла (см.). Увеличивая давление, мы можем довести вещество в жидком состоянии до критической температуры, при которой оно внезапно все превратится в газ, так как выше ее возможно существование данного вещества лишь в виде газа.
Из сказанного следует, что для определения упругости П., насыщающих пространство при данной температуре, можно: 1) либо определять давление, под которым при данной темпер. жидкость кипит, либо 2) дать образоваться в замкнутом пространстве при данной темп. насыщающему это пространство количеству П. данной жидкости и измерить манометром избыток давления, производимые им исследования, произведенные по этим двум методам, показали: 1) что определенной закономерной зависимости между температурой и соответствующей ей упругостью нас. П. для всех жидкостей найти при настоящем положении науки нельзя. Посему ограничиваются составлением на основании результатов опытов эмпирических формул, связующих темп. с упругостью насыщенного П. Так, напр., для воды дан был целый ряд формул Августом (1828), Реньо (1843) и другими. Формула Августа, дающая в пределах 0°—100° результаты весьма близкие к результатам опыта, следующая: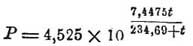
Приводим еще (по Цейнеру) формулы для упругости П. эфира, хлороформа и ртути: если выражать температуру t в градусах Цельсия, а упругость Р в мм ртутного столба то ход изменения Р можно выразить формулой
logP = a + b α t + c β t
Для эфира logP = 5,0286298 — bα t + c β t
где log(bα t) = 0,4414317 — 0,0031223t
log(c β t) = 0,6502970 — 4 + 0,0145775t
Для хлороформа logP = 5,2253893 — bα t — c β t
где log(bα t) = 0,5219943 — 0,0025856t
log(c β t) = 0,888617 — 1 — 0,0131824t
Для ртути logP = 5,6640459 — bα t + c β t
где log(bα t) = 0,890208 — 0,0012438t
log(c β t) = 0,5820395 — 1 — 0,0119062t
Подробные данные об упругости паров воды при разных температурах и плотности и удельном объеме водяных паров см. Zeuner, "Technische Thermodynamik" (т. II).
2) Упругость насыщенного П. сильно зависит от чистоты жидкости; небольшая примесь растворенного в ней другого тела заметно влияет на упругость насыщенного П. Это явление изучено особенно внимательно для растворов солей. Приводимая таблица дает, как пример, упругости П. растворов едкого кали в воде для нескольких концентраций и нескольких температур.
Содержание едкого кали в растворе в %.
| Темп.°С | 0% | 10% | 20% | 30% | 40% | 49% |
| 10° | 9,17 | 8,62 | 8,01 | 7,31 | 6,50 | 5,62 |
| 16° | 13,54 | 12,74 | 11,85 | 10,82 | 9,62 | 8,33 |
| 21° | 18,50 | 17,42 | 16,22 | 14,82 | 13,20 | 11,44 |
| 26° | 24,99 | 23,55 | 21,94 | 20,07 | 17,89 | 15,53 |
| 31° | 33,41 | 31,51 | 29,38 | 26,91 | 24,03 | 20,91 |
| 33° | 37,41 | 35,30 | 32,93 | 30,18 | 26,97 | 23,50 |
Новейшая теория растворов (см.) дали возможность теоретически вывести замечательную зависимость между упругостью насыщенного П. растворителя р 0 и раствора р для слабых растворов тел, не имеющих заметной упругости П. Если на 100 молекул растворителя приходится N молекул растворенного вещества, то, как показал Рауль (1888),
(p0 — p)/p0 — KN,
где K должно, по теории, равняться 0,01 и не должно зависеть от вещества растворителя. Опыты показали, что эта зависимость подтверждается при слабых растворах для большинства растворенных тел — не солей; для солей же K больше, что зависит от разложения соли в растворе (на ионы; см. Растворы). Упругость П. смеси двух жидкостей (р), имеющих каждая свою упругость насыщенного П. (p1 и р 2), обыкновенно (но не всегда) лежит между p1 и р 1; смеси жидкостей изучены были в этом отношении особенно подробно Д. П. Коноваловым (см. Кипение). Теоретические исследования на почве механической теории тепла показали, что упругость насыщенных П. должна зависеть еще от некоторых обстоятельств, а именно: 1) от формы поверхности, над которой П. образуется. Томсон (1871) первый показал, что над выпуклой поверхностью упругость П. всегда должна быть больше, чем над плоской, над вогнутой меньше; этот вывод был подтвержден опытами Винкельмана. Разница эта весьма невелика; напр. над каплей воды в 0,1 мм радиусом упругость П. лишь на 0,01 мм ртутного столба больше нормальной. Несмотря на эту небольшую разницу, явление это играет, по-видимому, значительную роль в природе; оно объясняет конденсацию мельчайшей водяной пыли в большие капли дождя. 2) От электризации поверхности жидкости упругость П. над ней понижается (весьма незначительно). Это явление может послужить для объяснения большого размера дождевых капель из грозовых облаков. Эти указанные два случая изменения упругости насыщенных П. являются, как показал проф. П. А. Шиллер (1895), частными случаями, подчиненными общему закону, гласящему, что упругость насыщенного П. увеличивается, когда на поверхность раздела жидкости и П. прилагается давление, направленное вовнутрь жидкости, и уменьшается, когда это давление направлено вовнутрь П.; по той же причине, как показал проф. Шиллер, упругость насыщенного П. жидкости, находящейся в среде газа под большим давлением, больше нормальной (в пустоте); таким образом, давление, приложенное к поверхности раздела П. и жидкости, как бы выдавливает из последней пары.
Если некоторый объем, насыщенный при данной температуре паром, нагреть, то П. будет перегретый и не насыщающий пространство, потому что при более высокой температуре для насыщения данного объема потребовалось бы большее количество П. То же самое произойдет, если при постоянной температуре увеличить объем, занимаемый П; его будет недостаточно для насыщения пространства, кроме того, он будет при более высокой температуре, чем та, при которой то же количество П. могло бы насытить этот больший объем, а следовательно, может быть назван перегретым. Чем больше П. перегрет и не насыщает пространство, тем больше он подобен газу и тем больше следует основным законам газов — закону Бойля-Мариотта и закону Гей-Люссака; наоборот, по мере приближения к условиям насыщения, отступления П. от следования указанным законам будут делаться все заметнее, а именно: произведение из давления на объем не будет величина постоянная, но будет непрерывно уменьшаться по мере приближения к насыщению, а коэффициент расширения (при постоянном давлении; см. Газы), равный в сильно перегретом П. коэффициенту расширения газа (0,00366), по мере приближения к насыщению П. будет быстро расти. В приводимой ниже таблице даны средние коэффициенты расширения водяного пара в различных температурных пределах.
Средние коэффициенты расширения (при пост. давлении) водяного пара.
| От 0° до 118° | 0,004187 |
| " 0° " 141° | 0,004189 |
| " 0° " 162° | 0,004071 |
| " 0° " 200° | 0,003938 |
| " 0° " 246° | 0,003799 |
(коэффициент расширения газов равен 0,00366).
Плотностью П. сильно перегретых и не насыщающих пространство, подобно плотности газов, называется отношение веса некоторого объема данного П. к весу одинакового объема воздуха, находящегося при тех же условиях температуры и давления, что и П.; плотность ненасыщенного П. может считаться не зависящей от температуры и упругости настолько, насколько П. эти следуют законам Бойля-Мариотта и Гей-Люссака и насколько они при этом не претерпевают химических изменений. По мере приближения к условиям насыщения пространства плотность П. растет и при насыщении достигает наибольшей величины, называемой плотностью насыщенного П. В нижеследующей таблице даны плотности П., далеких от насыщения, для некоторых тел.
Плотность паров различных веществ (отнесены к воздуху при тех же условиях).
| Хлор | 2,45 |
| Йод (250°— 600°) | 8,78 |
| Бром | 5,40 |
| Мышьяк | 10,36*) |
| Фосфор (300°—1000°) | 4,39 |
| Ртуть | 6,93 |
| Сера (выше 800°) | 2,21**) |
| Эфир | 2,56 |
*) Это число отвечает темп. краснокалильного жара и ниже, при 1714°—1736° плотность П. мышьяка почти вдвое меньше (см. Мышьяк).
**) При 450°—700° плотность П. серы 6,6 (см. Сера).
П. вещества, достаточно далекий от насыщения, представляет данное вещество в газообразном состоянии; в этом состоянии вещество должно следовать закону Авогадро — в одинаковых объемах газов заключается одинаковое количество молекул, — а следовательно, плотность П. должна быть пропорциональна весу молекул, или молекулярному весу вещества. Определение плотности II. далекого от насыщения представляет, таким образом, удобный способ определения молекулярного веса вещества и часто применяется для этой цели в химии (см. ниже).
Определение плотности насыщенного П. с удовлетворительной точностью в первый раз произведено было Ферберном и Тэтом (1861). Эти определения представляют интерес в том отношении, что позволяют проверить выводимую в механической теории тепла зависимость
V = v + EL/[T(dp/dT)]... A
где V удел. объем насыщенного П. (объем единицы веса), v удельный объем жидкости, L — скрытая теплота парообразования, Т абсолютная температура, dp/dT — изменение давления р с изменением температуры T, E — механический эквивалент тепла (425 кг м). Опыты Гервига (1869), Вюлльнера (1880), Перо (1888) и Бателли (1893) вполне подтвердили эту зависимость. Так, напр., для насыщенного водяного П. при 760 мм и 100° формула дает объем одного килограмма П. равным V = 1,6534 куб. м; объем одного килограмма воздуха при тех же условиях равен 1,0565 куб. м; следовательно, плотность водяного П. равна 1,0565/1,06584 = 0,6390. Перо же из опыта нашел при 99,6°C V = 1,657, что дает плотность 0,6386, т. е. очень близкий результат.
Если имеющийся при некоторой температуре некоторый объем П., насыщающего пространство, охладить до темп. t', которая меньше t, то явится избыток П., который осядет в виде капель жидкости; то же самое произойдет, если при постоянной темп. уменьшить объем, занимаемый П. (сжать П.). Даже П., не насыщающий пространство, при понижении его температуры можно довести до насыщения, после чего при дальнейшем понижении температуры он будет оседать в виде капель. Температура, при которой П. начнет оседать в виде капель, называется температурой росы, его упругость равна упругости насыщенного П. при температуре росы. Этими данными пользуются при определении количества влаги в воздухе (см. Влажность, Гигрометры). В последнее время (1895) Кантор указал на то, что температура росы при данных условиях зависит от поверхности, на которую П. оседает: она выше на поверхности, смачиваемой данной жидкостью, чем на поверхности, не смачиваемой ею.
На образование П. из жидкости — на разъединение частиц жидкости — требуется некоторая работа, которая доставляется обыкновенно жидкости, при испарении ее, в виде тепла. Это тепло притекает к жидкости либо извне (когда мы испаряем жидкость, нагревая ее), либо когда внешнего притока тепла нет, берется из самой жидкости, при чем жидкость охлаждается. Напр. все тепло, притекающее к кипящей на огне воде, имеющей 100°С, идет на образование П., и потому темп. воды во все время кипения не повышается; эфир, испаряющийся на воздухе, охлаждается вследствие испарения. Количество тепла, выраженное в калориях, необходимое для того, чтобы один килограмм жидкости перевести в П. при той же температуре, называется (скрытой) теплотой парообразования. В приводимой ниже таблице дана абсолютная температура кипения (температура по шкале Ц. + 273, напр. для воды 100 + 273 = 373) Т и теплота парообразования L для ряда веществ.
Теплота парообразования
| Т | L | М | ML/T | |
| Вода H 2O | 373,0 | 536,0 | 18 | 25,8 |
| Бензол С 6H6 | 853,0 | 92,9 | 78 | 20,5 |
| Хлороформ СНС l3 | 333,9 | 58,5 | 119 | 20,9 |
| Сероуглерод CS 2 | 319,1 | 83,8 | 76 | 20,0 |
| Ртуть Hg | 623,0 | 62,0 | 200 | 19,9 |
| Сера S | 589,0 | 862,0 | 82 | 19,6 |
Троутон (1884) указал на замечательную зависимость между молекулярным весом тел М, их абсолютной температурой кипения Т и теплотой парообразования L, а именно на то, что произведение ML/T есть величина для всех тел постоянная, близкая к 20, что и видно приблизительно из вышеприведенной таблицы. С повышением температуры почти у всех жидкостей теплота парообразования уменьшается. Так, напр., у воды (по данным Реньо) зависимость между температурой t и теплотой L выражается между 0° и 200° формулой
L = 589—0,3997t — 0,00124642,
что дает:
Теплота парообразования воды.
| Темп. | L | Темп. | L | Темп. | L |
| 0° | 589 | 75° | 552 | 150° | 501 |
| 25° | 578 | 100° | 547 | 175° | 481 |
| 500 | 566 | 125° | 520 | 200° | 459 |
Зависимость L от температуры может быть определена и теоретически, по приведенной выше формуле (А).
Свойства паров. Мы уже рассматривали коэффициент расширения П., уменьшающийся по мере удаления от температуры насыщения и приближающийся постепенно к коэффициенту расширения газов 0,00366. Теплопроводность П., как и газов, весьма незначительна; это наглядно следует из опытов над сфероидальным состоянием (см.). Определение теплоемкости (см.) ненасыщенных П. производится как и определение теплоемкости газов, причем определяется теплоемкость при постоянном давлении (см. Газ). Работы Реньо (1862) н Е. Видемана (1876) показали, что теплоемкость П. меньше, чем теплоемкость соответствующих жидкостей, причем отношение теплоемкости жидкости к теплоемкости П. у большинства жидкостей равно приблизительно 1,7. С повышением температуры теплоемкость П., как и жидкостей, повышается, причем приблизительно в той же мере, как и жидкостей. Если выражать теплоемкость жидкости через C1, пара через С 2, а зависимость их от температуры формулой
C1 = C01 + a1t,
C2 = C02 + a2t,
то нижеследующая таблица дает (по Е. Видеману) эти величины для различных жидкостей.
Теплоемкость жидкостей и их паров (по Е. Видеману).
| Хлороформ | Серн. углерод | Эфир | Бензин. | |
| Пар | 0,1341 + 0,0000677t | 0,1315 + 0,0000963t | 0,3725 + 0,0004268t | 0,2237 + 0,0005114t |
| Жидкость | 0,2323 + 0,0000507t | 0,2352 + 0,0000815t | 0,5290 + 0,0002958t | 0,3798 + 0,0007200t |
Клаузиус (1850) ввел еще понятие о теплоемкости насыщенного П. т. е. о том количестве тепла, которое нужно придать единице массы насыщенного П., чтобы нагреть его на 1°, если в то же время настолько П. сжимать, чтобы сохранить его насыщенным. Теоретическое исследование этой теплоемкости привело к результату, что она может быть как положительной, так и отрицательной, т. е. что количество работы, необходимое для того, чтобы настолько сжать нагретый П., чтобы он снова пришел к состоянию насыщения, может быть, будучи превращено в эквивалентное количество тепла, больше тепла, приданного П. для его нагревании и меньше его. Прямым следствием отсюда является, что насыщенный П., обладающий положительной теплоемкостью, будучи быстро [Чтобы не было извне притока или оттока тепла.] сжат, частью осядет в виде жидкости — и перегреется, будучи быстро разрежен; насыщенный П., обладающий отрицательной теплоемкостью, наоборот, будучи быстро сжат, перегреется, а будучи быстро разрежен, осядет в виде росы. Теплоемкость насыщенных П. воды отрицательная, у эфира она положительная. Вероятно, у всех веществ есть температура, при которой теплоемкость насыщенных П. их меняет знак; такая перемена знака наблюдалась у хлороформа при 140° и у бензина при 115°. Оптические свойства П. весьма близки к таковым же свойствам газов; коэфф. преломления их при нормальном давлении весьма, мало отличается от единицы; наибольший у П. сернистого углерода — около 1,0015. Светорассеяние П. весьма незначительное, и до 1865 г. даже сомневались в его существовании; некоторые П., напр. П. йода, обладают аномальным светорассеянием (см.). Электропроводность у П. весьма малая и, по-видимому, электролитическая, т. е. основана на разложении молекул П.; это подтверждается наблюдением, что одноатомные П., напр. П. ртути, не проводят электричества; этот сложный вопрос еще мало разработан. Диэлектрическая постоянная П. близка к единице и не вполне следует закону Максвелла, по которому диэлектрическая постоянная тела должна быть пропорциональна квадрату коэфф. преломления света этим телом. Вообще можно сказать, что свойства П. сильно зависят от степени их перегретости и в сильно перегретых П. приближаются к свойствам газов, в насыщенных же П. заметно от них отличаются.
А. Гершун.
Определение плотности П. играет большую роль в химической практике, так как оно служит одним из важнейших способов для нахождения молекулярного веса химических соединений. Закон Авогадро-Жерара гласит что для тел в парообразном состоянии при одних и тех же условиях в равных объемах заключается равное число частиц, так что частичные веса различных тел относятся, как плотности их П. Определение плотности П. вещества, указывая его частичный вес, дает возможность, пользуясь данными для его процентного состава, определить его химическую формулу. Требуется только, чтобы определение плотности П. производилось в таких условиях, в которых вещество не претерпевало бы никаких химических изменений и являлось со своими нормальными свойствами. Определение плотностей П. производится вообще при атмосферном давлении и при температурах, которые на 20°—30° выше темпер. кипения исследуемого вещества, чтобы быть уверенным, что оно все обратилось в П.; но в некоторых случаях полезно бывает производить определение плотности П. при низшем давлении и темпер., напр. для веществ труднолетучих и от нагревания разлагающихся; иногда полезно делать это в присутствии других веществ, напр. когда к веществу диссоциирующему примешивается заранее один из продуктов его распада для уменьшения его разложения и пр. Все многочисленные способы определения плотности П. можно разделить на две категории: в одной определяется, какой объем занимает в П. при данных условиях известное количество вещества, напр. способы В. Мейера, Гофманна, Гей-Люссака и пр. В другой отыскивается вес вещества в П., при данном объеме, напр. способ Дюма. Наибольшим распространением пользуется способ В. Мейера. Хотя по точности он, может быть, и уступает способу Дюма, но необыкновенная простота и легкость выполнения делают его незаменимым в лабораториях.
Способ В. Мейера основывается на том, что вещество, быстро обращаясь в П. в сосуде, наполненном каким-либо нагретым газом, вытесняет объем его, равный объему своего П. при данных условиях темп. и давления. Если известен вес обращенного в П. вещества s и измерен объем вытесненного газа, то стоит только вычислить вес последнего g, и получатся все данные для вычисления искомой плотности пара
Δ /d = s/g
где d плотность газа. Как видим, знать температуру среды, при которой вещество обратилось в П., и давление, в ней господствующее, — излишне, лишь бы эта величина не изменилась в течение опыта, что при его кратковременности достичь очень легко. Все это представляет громадное преимущество этого способа перед другими. Прибор В. Мейера (ф. 1) состоит из тонкостенного цилиндра b, около 200 куб. см емкости, с длинной (около 600 мм) стеклянной трубкой около 4 мм диам.
Фиг. 1. Прибор Мейера.
Трубка имеет в верхней части две боковых трубочки h и i; одна из них, капиллярная i, соединенная каучуком с f, служит для выхода газа; в другой
| "БРОКГАУЗ И ЕФРОН" >> "П" >> "ПА" >> "ПАР" >> "ПАРФ" |
Статья про "Пар физ.-хим." в словаре Брокгауза и Ефрона была прочитана 4727 раз
| Бургер двойного помола |
| Луковый соус |
TOP 15
- Волос
- Проно
- Степные животные
- Гимнастика
- Индийский океан
- Архитектура
- Сравнение, в литературе
- Манда
- Клитры
- Колесование
- Испарение
- Травоядные животные
- Оплодотворение у pacтений
- Вредные насекомые
- Электризация тел