


БНБ
"БРОКГАУЗ И ЕФРОН" (121188)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Остаток интегральный
Определение "Остаток интегральный" в словаре Брокгауза и Ефрона
Остаток интегральный — Если z = x + y√ (—1) есть мнимое переменное и дано W = f(z), то интеграл: 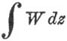 , взятый по замкнутому контуру, содержащему точку z = а, при которой f(z) претерпевает перерыв, равен 2π p √(—1), где p = Sinz = а [(z — a)f(z)]; величина
, взятый по замкнутому контуру, содержащему точку z = а, при которой f(z) претерпевает перерыв, равен 2π p √(—1), где p = Sinz = а [(z — a)f(z)]; величина 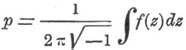 и называется интегральным О. (см. Мнимые величины).
и называется интегральным О. (см. Мнимые величины).
H. Делоне.
| "БРОКГАУЗ И ЕФРОН" >> "О" >> "ОС" >> "ОСТ" >> "ОСТА" |
Статья про "Остаток интегральный" в словаре Брокгауза и Ефрона была прочитана 961 раз
| Пицца в сковороде |
| Панайпай |
TOP 15
- Волос
- Проно
- Степные животные
- Гимнастика
- Индийский океан
- Архитектура
- Сравнение, в литературе
- Манда
- Клитры
- Колесование
- Испарение
- Травоядные животные
- Оплодотворение у pacтений
- Вредные насекомые
- Электризация тел