


БНБ
"БРОКГАУЗ И ЕФРОН" (121188)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Определитель
Определение "Определитель" в словаре Брокгауза и Ефрона
Определитель (Determinant). — Решая два уравнения первой степени с двумя неизвестными: а 1 х + b1 у = c1, а 2 х + b2 у = c2, получаем следующие выражения для x и у: x = (c1b2 — c2b1)/(a1b2 — a2b1), y = (a1c2 — a2c1)/(a1b2 — a2b1). Подобным же образом, решая три уравнения первой степени с тремя неизвестными, получим выражение последних в виде отношений многочленов, составленных из постоянных, входящих в уравнения. Например, многочлен, стоящий в знаменателях, будет: a1b2c3 — a1b3c2 + a2b3c1 — a2b1c3 + a3b1c2 — a3b2c1. Многочлены такого вида называются определителями и обозначаются особыми символами; так: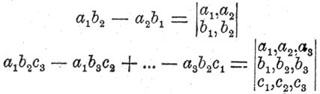
Свойства О. и действия над ними рассматриваются в алгебраическом анализе. Многие сложные вычисления значительно упрощаются при пользовании О. В высшем анализе приходится пользоваться так называемыми функциональными О., составленными из производных от функций, зависящих от нескольких переменных; таков, напр., функциональный определитель: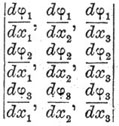
Трех функций φ 1, φ 2, φ 3 от трех переменных х 1, x2, x3. Есть на всех языках сочинения, заключающие теорию О. См. Ващенко-Захарченко, "Теория определителей"; Baltzer, "Th éorie et application des déterminants".
Д. Б.
| "БРОКГАУЗ И ЕФРОН" >> "О" >> "ОП" >> "ОПР" |
Статья про "Определитель" в словаре Брокгауза и Ефрона была прочитана 809 раз
| Коптим скумбрию в коробке |
| Каракатица на гриле |
TOP 15
- Волос
- Проно
- Степные животные
- Гимнастика
- Индийский океан
- Архитектура
- Сравнение, в литературе
- Манда
- Клитры
- Колесование
- Испарение
- Травоядные животные
- Оплодотворение у pacтений
- Вредные насекомые
- Электризация тел