


БНБ
"БРОКГАУЗ И ЕФРОН" (121188)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Нумерация
Определение "Нумерация" в словаре Брокгауза и Ефрона
Нумерация (лат. numeratio) — приложение законов образования чисел в употребляемых системах счисления к выражению числа словом — словесная Н. или письменными знаками — письменная Н. Последовательно развились формы счисления 5-ричной, 10-ричной и 20-ричной систем для целых чисел и форма 2-ичной системы для чисел меньших единицы (см. соотв. статью). Общая система счисления может быть определена, как такая группировка целых и дробных чисел, при которой каждое из них представляется формулой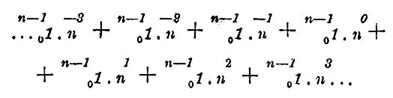 ,
,
в которой п означает основное число системы счисления, а символ 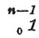 какое-нибудь из чисел, происшедших от умножения 1 на 0, 1, 2, 3,..., п —1. Выражение числа словом, как показывает существование во многих языках двойственного числа, началось в ту отдаленную эпоху, когда доступная человеческому сознанию область счисления ограничивалась определенными представлениями единицы и два и неопределенным — множества. Названиями первых четырех чисел были или имена предметов, всегда встречающихся человеку в соответствующем количестве, или же соединения названий меньших чисел по схемам образования из них выражаемых больших чисел, вроде употребляемых многими из племен современных дикарей выражений два-один для обозначения 3, два-два для обозначения 4. Первые в течение громадных промежутков времени, отделяющих начало их употребления от близких к нам эпох, до того изменились, что в настоящее время представляются совершенно первообразными словами, утратившими всякую связь с другими. Вторые, как основанные не на посторонних для счисления отношениях, а на нем самом, оказались более способными сохранять свои первоначальные формы. С последовавшим после выделения представления числа 5 переходом счисления к пальцевому счету — его развитие сделалось настолько быстрым, что первобытные языки со своими скудными средствами выражения новых понятий не оказались в состоянии следить за ним, и словесная Н. стала все более и более отставать от пальцевого счета. Чтобы пособить себе в этом трудному положении первобытным языкам не оставалось ничего другого, как воспользоваться для словесного выражения чисел названиями соответствующих предметов или действий в пальцевом счете, то есть перейти к употреблению пальцевых числительных. Свод в одно целое многочисленных фактов, представляемых языками современных полудиких и варварских племен, представляет образование системы этих числительных в следующих характеристичных чертах. Число 5 выражается словом рука или половина рук, 6 — словами один на другой руке или половина рук и один, 7 — два на другой руке или половина рук и два и т. д., 10 — словами две руки или реже полчеловека, 11 — один на ноге или нога один, 12 — два на ноге или нога два и т. д., 15 — словами целая нога или рука на каждой стороне и половина ног, 16 — один на другой ноге и т. д., 20 — словами один человек или даже целым предложением "один человек кончен" или "наружные члены человека кончены", 21 — словами один на руке другого человека и т. д., 40 — словами два человека, 60 — словами три человека и т. д. В виде удержавшихся доныне следов отдаленного прошлого некоторые из пальцевых числительных встречаются и в языках цивилизованных народов. Когда же после выделения представления числа 20 или и ранее после выделения представления числа 10, исключительное употребление при счете ручных и ножных пальцев в первом случае и одних ручных во втором должно было по разным представляемым им неудобствам прекратиться, тогда языки и по слабости человеческой памяти, и по собственной бедности в средствах образования новых слов стали лицом к лицу с вопросом, как достигнуть выражения хотя бы только употребительных в обыденной жизни чисел посредством возможно меньшего количества различных слов. Решение этого вопроса, поставленное вне генетического развития, может быть, было бы затруднительным даже для современного человечества, не только для первобытного человека, если бы к нему не пришли на помощь системы счисления со своими законами образования чисел. Эти последние действительно дают возможность уменьшить количество требуемых для выражения чисел различных слов в очень значительной степени. В самом деле, соединяя считаемые предметы или вообще единицы в группы, содержащие их каждая в количестве, равном основному числу системы, собирая затем эти группы, или группы первого порядка, в группы второго, содержащие первые опять-таки в количестве, равном основному числу системы, и продолжая таким же образом далее до получения групп какого-нибудь из высших порядков в количестве, меньшем основного числа, всякая система счисления требует для выражения чисел только названий для первых, меньших основного числа, количеств единиц и затем для всех групп от первого порядка до высшего из употребляемых. Это количество различных не зависимых одно от другого слов может быть еще уменьшено, если составлять названия групп различных порядков из названия основного числа по схемам образования из него их единиц. Применяя тот же прием к составлению названий как самого основного числа, так и меньших его чисел, из названия единицы по схемам их образования из нее, можно даже придти к исключительному употреблению названия только ее одной. Сложность, неуклюжесть и неясность таких составных названий помешали языкам осуществить все указанные возможности на деле. В общих чертах образование числительных происходило в следующем виде. Числа, меньшие основного числа п системы, т. е. 1, 2, 3,..., п—1, выражались или отдельными независимыми друг от друга названиями, или, начиная с 6, названиями, составленными из названий предыдущих чисел по законам системы счисления с меньшим основным числом (5-ричной при употреблении 10-чной, 5-ричной или 10-чной — при 20-ричной). Обстоятельством, определившим ход образования названий для непосредственно следующих за основним числом чисел n + 1,..., n×n + n — 1 было распадение их на две группы: на числа, в образовании которых участвует сложение и которые, поэтому, могут быть названы составными числами, и на числа, образуемые исключительно действием умножения и потому являющиеся кратными основного числа (напр. 2 n, 3n и т. д.). Строение числительных имен в этих двух группах хотя и пользуется одними и теми же названиями основного числа и чисел меньших его, но резко различается во всех языках формами соединения этих названии друг с другом, напр. тринадцать и тридцать, dreizehn и dreissig и т. д. Обе эти формы по предметам, с которыми они имеют дело, могут быть названы: одна — слагательной, другая — множительной. Строго разграниченное, не допускающее свободного выбора употребление каждой из этих двух форм продолжалось только до образования числительного, выражающего число п × п + п. Так как кроме этого вида, принадлежащего к слагательной форме, то же число может быть представлено еще и в виде (n + 1)×n, принадлежащем к множительной, то перед языками предстал вопрос: какому из этих двух видов отдать предпочтение? Решение в пользу первого вида было опять таки подсказано языкам системами счисления, для которых числу п × п в группе второго порядка принадлежало такое же значение, как самому основному числу в группе первого порядка, т. е. значение единицы соответствующего порядка, или, что то же самое, разряда, чисел. Что же касается происхождения последнего понятия, то в пальцевых системах счисления оно было таково. При счете большого числа предметов человеку приходилось делать много внешних заметок для обозначения последовательно получаемых чисел, равных основному числу системы счисления. Считать эти заметки человек опять-таки мог только по пальцам, причем, дойдя до основного числа системы, он должен был делать новую заметку, которая обозначала теперь уже n×n. Для словесного выражения единиц разрядов языки пользовались или названиями, независимыми друг от друга, вроде древнерусских сто, тысяча, тьма (10000), легион или несвед (100000), леодр (1000000), вран (10000000) и колода (100000000), или названиями смешанными, представляющими образование выражаемых единиц разрядов из предыдущих, вроде русских: десять тысяч, сто тысяч и т. д. Сложившееся в языках в указанном сейчас виде решение приведенного выше основного вопроса словесной Н. удовлетворяет, очевидно, только минимуму предъявляемых им требований. Максимум же их состоит в выражении числа самым кратким и ясным образом с помощью строго ограниченного и притом возможно меньшего количества независимых друг от друга слов. Решение того же вопроса на основании указаний систем счисления, при недопущении каких бы то ни было отступлений от них, удовлетворяет указанному максимуму во всем, кроме требования краткости, как это можно видеть на деле, если заняться составлением названий единиц разрядов из названия основного числа и названий последнего и предшествующих ему меньших чисел из названия единицы на основании законов их образования. Стремление к устранению этого важного недостатка решения и было причиной, заставившей языки пожертвовать другим важным требованием вопроса — строгой ограниченностью количества независимых друг от друга числительных. Народ, далее всех ушедший в развитии счисления и потому глубже других проникший в практические условия образования словесной Н., т. е. индусы, кончил это образование выражением всех единиц разрядов отдельными друг от друга названиями. Этим он пришел в противоположность требованиям вопроса к необходимости употребления бесконечного числа независимых друг от друга названий для выражения бесконечного множества чисел. Народы, менее подвинувшиеся в счислении, будучи заинтересованы только той узкой его областью, которая определяется обыденными житейскими нуждами, избрали средний путь. Давая независимые друг от друга названия только единицам некоторых разрядов и обозначая другие выражениями, составленными из этих названий на основании законов образования чисел, они достигали не устранения бесконечности независимых друг от друга числительных, а только уменьшения их в области, эксплуатируемой общежитием. Но и это уменьшение достигалось ими в ущерб краткости. В результате, и у индусов, и у народов, избравших средний путь, употребляемые формы решения основного вопроса словесной Н. оказывались удовлетворяющими минимуму его требований; идеал же оставался по-прежнему не достигнутым. Наблюдениям над словесною Н. у разных народов история происхождения и последующего развития счисления обязана главной частью своего материала. В настоящее время, в полном виде или в виде следов и остатков прежнего употребления, 5-ричная система счисления употребляется у 26 племен Африки, 8 — Полинезии, 13 — Азии и 30 — Америки; 20-ричная у 4 племен Африки, 3 — Полинезии, 18 — Азии, 8 — Америки и 6 — Европы. Что же касается 10-ричной системы, то частью вследствие некоторых выгод, доставляемых ее употреблением для словесной и письменной Н., главным же образом вследствие употребления ее народами, стоявшими во главе умственного движения человечества, она сделалась в настоящее время единственно употребляемой во всех цивилизованных обществах, и делаемые в настоящее время предложения ее замены другими будто бы более удобными системами счисления (напр. 12-ричной) едва ли могут быть считаемы вызванными какими-нибудь нуждами дела. Вызванное появлением систем счисления начало употребления письменной Н. (см. Математика) было в то же время и началом употребления письма вообще, как об этом согласно свидетельствуют, с одной стороны, те из современных дикарей, которые, видя впервые процесс письма, обозначают его глаголом "считать", а с другой — те из языков цивилизованных народов, в которых действия письма и счета обозначаются одним и тем же глаголом. Два рода предметов, употребляемых в качестве первых письменных знаков для обозначения основных чисел систем счисления (камни и подобные им предметы и штрихи, проводимые на песке или красящим веществом на какой-нибудь поверхности), направили развитие письменной Н., а вместе с ним и самого письма, по двум путям. Первый из этих путей повел ее от первоначального пользования камнями (латинское calculare — считать от calculus — камешек) к столь распространенному в Китае и у туземных племен Южной Америки, а также и у многих народов Африки и Австралии, употреблению шнурков с узлами, которое, как особая форма письма вообще, достигло своего наивысшего развития в перуанском квипусе. Первыми формами, усвоенными письменной Н. при следовании по второму пути, были бирка и системы знаков живописного письма. Затем вместе с самим письмом письменная Н. прошла и через все последующие стадии его развития, представляемые иероглифическим письмом, иератическим, клинообразным и, наконец, звуковым. Из трех форм, в которых представляется или может быть представлено письмо в настоящее время, словесной, звуковой и идейной (Begriffsschrift), письменная Н. с очень раннего времени примкнула к идейной, то есть именно к той, которая для письма вообще представляет еще его будущую форму, как это можно видеть из самого понятия идейного письма, знаки которого должны быть символами основных элементарных понятий, соединяемыми для выражения сложных, на основании законов, управляющих образованием последних из первых в действительности. Своим ранним переходом к этой высшей будущей форме письма письменная Н. обязана простоте содержания счисления. В то время как в других областях человеческого знания числа основных элементарных понятий, а также и родов их сочетания, говоря вообще, весьма значительны, в области счисления основное элементарное понятие только одно — понятие способной к повторению в каком угодно числе раз единицы; родов же сочетания, известных под именем основных арифметических действий, не более четырех (даже можно считать двух). Идеал письменной Н., как одного из частных случаев идейного письма, состоит в самом кратком и ясном, с помощью возможно меньшего количества произвольных знаков, выражении всякого числа по его понятию, то есть по его образованию в системе счисления. В бессознательном стремлении к этому идеалу человечество в разные эпохи и в лице разных народов изобрело множество более или менее различающихся между собой систем числовых знаков, или цифирных систем, если называть числовые знаки вообще цифрами. Все эти системы в сущности суть только более или менее удачные попытки решения следующих двух основных вопросов развития письменной Н.: как выразить разряды системы счисления? как представить кратные единиц этих разрядов? Первоначальным решением этих вопросов, доставленным естественными ходом развития, было для первого — обозначение единиц разрядов особыми знаками и для второго — помещение этих знаков рядом в требуемом количестве, меньшем, чем основное число системы, или так называемый аддитивный метод. Как естественные, вполне выражающие в своей области образование сложных понятий из элементарного, эти решения принимали участие в образовании всех последующих цифирных систем, носящих на себе тем более заметные следы деятельности человеческого разума, чем к более позднему времени они принадлежали. Обозначение единиц разрядов особыми знаками удерживалось почти до самого конца развития письменной Н. Аддитивный же метод, рассматриваемый в смысле выражаемого им общего принципа и потому не ограничиваемый одним выражением кратных единицам разрядов, составляет основную схему изображения числа во всякой цифирной системе, не исключая и той, которая закончила собой развитие письменной Н. Проникающий, по сказанному, все цифирные системы, аддитивный принцип не определял, однако, порядок размещения разрядов в изображении чисел, который был для него совершенно безразличным. Не таковым, однако же, оказался этот порядок для умственной природы человека, установившей во всех без исключения известных нам цифирных системах один и тот же общий принцип следования меньших разрядов за большими в направлении письма. Значительность количества знаков, требуемых аддитивным методом для выражения кратных единицам разрядов, повела к многочисленным попыткам изыскания средств ее устранения. Одни из этих попыток не получили дальнейшего развития и представляются теперь только в виде следов употребления представляемых ими методов (вычитающий метод римлян, делительный — ацтеков). Напротив, другие развивались и в виде обработанных вполне или отчасти методов получали более или менее значительное распространение. Из них ближайшим по идее к аддитивному методу и в то же время древнейшим был мультипликативный метод, состоящий в выражении кратного единицы какого-нибудь разряда в виде произведения этой единицы на соответствующее число разряда единиц. Знак этого последнего числа, для отличия от его употребления в значении слагаемого, всегда помещается относительно знака единицы разряда со стороны, противоположной направлению письма. Давая возможность выразить всякое кратное единицы какого-нибудь разряда только двумя знаками, мультипликативный метод делает значительный шаг вперед в сравнении с аддитивным методом. Встречаемым им на практике препятствием к полному осуществлению своей цели является многозначие в изображениях как единиц разрядов, так и чисел разряда единиц. В тех же случаях, когда те и другие изображаются независимыми друг от друга одиночными знаками, он достигает высшей доступной для него степени совершенства. Следующим по времени своего наибольшего развития и также достигавшим своей ближайшей цели вполне был метод обозначения кратных единицам разрядов особыми независимыми друг от друга знаками. Требуя для изображения кратного единицы разряда только один знак, этот метод идет далее мультипликативного, но в то же время значительно увеличивая общее число употребляемых в счислении знаков, он крайне затрудняет память. Это последнее обстоятельство делало невозможным сколько-нибудь значительное развитие рассматриваемого метода до самого того времени, когда в распоряжении человечества появился в виде алфавита ряд знаков, имеющих строго определенные порядок и значение. С этого времени метод получил очень широкое распространение, значительно превосходящее распространение мультипликативного метода. Ограниченность числа знаков, составляющих алфавит, делало его непосредственно применимым только к сравнительно очень небольшой области счисления, хотя в практике и особенно употребительной. Стремление к удержанию знаков алфавита и представляемых ими выгод и за пределами их непосредственного приложения к счислению выразилось на практике двумя важными последствиями. Чтобы вторично применить знаки алфавита или буквы к обозначению кратных единицам разрядов, следующих за теми, которые уже получили такое обозначение, пользующиеся ими народы прибавляли к буквам особый значок, напр. помещаемый снизу или сверху штрих или точку. Этот прием, делая, очевидно, безграничным приложение алфавита в методе обозначения особыми знаками, являлся в то же время первоначальной формой нового метода, который может быть назван указательным, как выражающий кратное единицы какого-нибудь разряда присоединением знака этой единицы в виде указателя к знаку соответствующего числа разряда единиц. Вторым последствием упомянутого выше стремления было появление в методе обозначения особыми знаками, а вместе с ним, и в указательном методе, идеи значения числового знака по занимаемому им месту, или, короче, идеи положения. Когда в изображении числа за первым употреблением знаков алфавита следовало второе, тогда не было никакой надобности в удержании указателей, так как вторичное числовое значение букв указывалось самим их местом. И действительно, во всех этих случаях значки указателей употребляющими их народами опускались. Употребление составленных по мультипликативному, или указательному, методу цифирных систем в письменном счете имело своим следствием образование нового метода выражения кратных единицам разрядов. При сложении, напр., большого количества многозначных чисел самый процесс совершения действий по разрядам приводил к помещению слагаемых одного под другим так, чтобы числа одного и того же разряда составляли один столбец. Отсюда было уже недалеко до мысли заменить для сокращения письма повторение в виде множителя или указателя знака единицы разряда при каждом из ее чисел помещением этого знака всего только один раз над принадлежащим ему столбцом. Для большей ясности и предупреждения возможных смешений чисел следующих друг за другом разрядов пришлось отделить упомянутые столбцы один от другого вертикальными линиями. Таким образом, постепенно сформировался новый метод столбцов, состоящий в изображении всякого числа помощью помещения чисел единиц составляющих его разрядов в разграфленных столбцах, над которыми в последовательном порядке и без всяких пропусков писались знаки единиц разрядов. Нетрудно видеть, однако же, что в этих знаках не было никакой существенной надобности, так как разряд, представляемый каким-нибудь из столбцов, определялся местом последнего в среде других. Таким образом, знаки единиц разрядов делались излишними, и на смену им выступало занимаемое разрядом в числе место, другими словами, идея положения впервые получала ясное и полное выражение. Вместе с тем, метод столбцов своими пробелами в изображениях чисел, не содержащих всех обнимаемых ими разрядов, ясно показывал, что для приложения этой идеи к практике необходимо обозначать каким-нибудь способом, пробелом или особым знаком, отсутствие в изображаемом числе того или другого из обнимаемых им разрядов, следствием чего и могло быть принадлежащее индусам введение нуля. Изобретение этого нового знака письменной нумерации дало индусам возможность ввести во всеобщее употребление представляемый идеей положения новый метод выражения кратных единицам разрядов, который поэтому и назыв. методом положения. Выразив с помощью знаков чисел, меньших основного числа употребляемой системы счисления, и нуля все числа уходящего в бесконечность их ряда, этот метод вполне осуществил идеал письменной нумерации и тем закончил развитие последней. От индусов этот метод вместе с характерной системой так назыв. "пыльных" цифр перешел к арабам, а от них в Зап. Европу, через посредство которой распространился и во всем цивилизованном человечестве.
какое-нибудь из чисел, происшедших от умножения 1 на 0, 1, 2, 3,..., п —1. Выражение числа словом, как показывает существование во многих языках двойственного числа, началось в ту отдаленную эпоху, когда доступная человеческому сознанию область счисления ограничивалась определенными представлениями единицы и два и неопределенным — множества. Названиями первых четырех чисел были или имена предметов, всегда встречающихся человеку в соответствующем количестве, или же соединения названий меньших чисел по схемам образования из них выражаемых больших чисел, вроде употребляемых многими из племен современных дикарей выражений два-один для обозначения 3, два-два для обозначения 4. Первые в течение громадных промежутков времени, отделяющих начало их употребления от близких к нам эпох, до того изменились, что в настоящее время представляются совершенно первообразными словами, утратившими всякую связь с другими. Вторые, как основанные не на посторонних для счисления отношениях, а на нем самом, оказались более способными сохранять свои первоначальные формы. С последовавшим после выделения представления числа 5 переходом счисления к пальцевому счету — его развитие сделалось настолько быстрым, что первобытные языки со своими скудными средствами выражения новых понятий не оказались в состоянии следить за ним, и словесная Н. стала все более и более отставать от пальцевого счета. Чтобы пособить себе в этом трудному положении первобытным языкам не оставалось ничего другого, как воспользоваться для словесного выражения чисел названиями соответствующих предметов или действий в пальцевом счете, то есть перейти к употреблению пальцевых числительных. Свод в одно целое многочисленных фактов, представляемых языками современных полудиких и варварских племен, представляет образование системы этих числительных в следующих характеристичных чертах. Число 5 выражается словом рука или половина рук, 6 — словами один на другой руке или половина рук и один, 7 — два на другой руке или половина рук и два и т. д., 10 — словами две руки или реже полчеловека, 11 — один на ноге или нога один, 12 — два на ноге или нога два и т. д., 15 — словами целая нога или рука на каждой стороне и половина ног, 16 — один на другой ноге и т. д., 20 — словами один человек или даже целым предложением "один человек кончен" или "наружные члены человека кончены", 21 — словами один на руке другого человека и т. д., 40 — словами два человека, 60 — словами три человека и т. д. В виде удержавшихся доныне следов отдаленного прошлого некоторые из пальцевых числительных встречаются и в языках цивилизованных народов. Когда же после выделения представления числа 20 или и ранее после выделения представления числа 10, исключительное употребление при счете ручных и ножных пальцев в первом случае и одних ручных во втором должно было по разным представляемым им неудобствам прекратиться, тогда языки и по слабости человеческой памяти, и по собственной бедности в средствах образования новых слов стали лицом к лицу с вопросом, как достигнуть выражения хотя бы только употребительных в обыденной жизни чисел посредством возможно меньшего количества различных слов. Решение этого вопроса, поставленное вне генетического развития, может быть, было бы затруднительным даже для современного человечества, не только для первобытного человека, если бы к нему не пришли на помощь системы счисления со своими законами образования чисел. Эти последние действительно дают возможность уменьшить количество требуемых для выражения чисел различных слов в очень значительной степени. В самом деле, соединяя считаемые предметы или вообще единицы в группы, содержащие их каждая в количестве, равном основному числу системы, собирая затем эти группы, или группы первого порядка, в группы второго, содержащие первые опять-таки в количестве, равном основному числу системы, и продолжая таким же образом далее до получения групп какого-нибудь из высших порядков в количестве, меньшем основного числа, всякая система счисления требует для выражения чисел только названий для первых, меньших основного числа, количеств единиц и затем для всех групп от первого порядка до высшего из употребляемых. Это количество различных не зависимых одно от другого слов может быть еще уменьшено, если составлять названия групп различных порядков из названия основного числа по схемам образования из него их единиц. Применяя тот же прием к составлению названий как самого основного числа, так и меньших его чисел, из названия единицы по схемам их образования из нее, можно даже придти к исключительному употреблению названия только ее одной. Сложность, неуклюжесть и неясность таких составных названий помешали языкам осуществить все указанные возможности на деле. В общих чертах образование числительных происходило в следующем виде. Числа, меньшие основного числа п системы, т. е. 1, 2, 3,..., п—1, выражались или отдельными независимыми друг от друга названиями, или, начиная с 6, названиями, составленными из названий предыдущих чисел по законам системы счисления с меньшим основным числом (5-ричной при употреблении 10-чной, 5-ричной или 10-чной — при 20-ричной). Обстоятельством, определившим ход образования названий для непосредственно следующих за основним числом чисел n + 1,..., n×n + n — 1 было распадение их на две группы: на числа, в образовании которых участвует сложение и которые, поэтому, могут быть названы составными числами, и на числа, образуемые исключительно действием умножения и потому являющиеся кратными основного числа (напр. 2 n, 3n и т. д.). Строение числительных имен в этих двух группах хотя и пользуется одними и теми же названиями основного числа и чисел меньших его, но резко различается во всех языках формами соединения этих названии друг с другом, напр. тринадцать и тридцать, dreizehn и dreissig и т. д. Обе эти формы по предметам, с которыми они имеют дело, могут быть названы: одна — слагательной, другая — множительной. Строго разграниченное, не допускающее свободного выбора употребление каждой из этих двух форм продолжалось только до образования числительного, выражающего число п × п + п. Так как кроме этого вида, принадлежащего к слагательной форме, то же число может быть представлено еще и в виде (n + 1)×n, принадлежащем к множительной, то перед языками предстал вопрос: какому из этих двух видов отдать предпочтение? Решение в пользу первого вида было опять таки подсказано языкам системами счисления, для которых числу п × п в группе второго порядка принадлежало такое же значение, как самому основному числу в группе первого порядка, т. е. значение единицы соответствующего порядка, или, что то же самое, разряда, чисел. Что же касается происхождения последнего понятия, то в пальцевых системах счисления оно было таково. При счете большого числа предметов человеку приходилось делать много внешних заметок для обозначения последовательно получаемых чисел, равных основному числу системы счисления. Считать эти заметки человек опять-таки мог только по пальцам, причем, дойдя до основного числа системы, он должен был делать новую заметку, которая обозначала теперь уже n×n. Для словесного выражения единиц разрядов языки пользовались или названиями, независимыми друг от друга, вроде древнерусских сто, тысяча, тьма (10000), легион или несвед (100000), леодр (1000000), вран (10000000) и колода (100000000), или названиями смешанными, представляющими образование выражаемых единиц разрядов из предыдущих, вроде русских: десять тысяч, сто тысяч и т. д. Сложившееся в языках в указанном сейчас виде решение приведенного выше основного вопроса словесной Н. удовлетворяет, очевидно, только минимуму предъявляемых им требований. Максимум же их состоит в выражении числа самым кратким и ясным образом с помощью строго ограниченного и притом возможно меньшего количества независимых друг от друга слов. Решение того же вопроса на основании указаний систем счисления, при недопущении каких бы то ни было отступлений от них, удовлетворяет указанному максимуму во всем, кроме требования краткости, как это можно видеть на деле, если заняться составлением названий единиц разрядов из названия основного числа и названий последнего и предшествующих ему меньших чисел из названия единицы на основании законов их образования. Стремление к устранению этого важного недостатка решения и было причиной, заставившей языки пожертвовать другим важным требованием вопроса — строгой ограниченностью количества независимых друг от друга числительных. Народ, далее всех ушедший в развитии счисления и потому глубже других проникший в практические условия образования словесной Н., т. е. индусы, кончил это образование выражением всех единиц разрядов отдельными друг от друга названиями. Этим он пришел в противоположность требованиям вопроса к необходимости употребления бесконечного числа независимых друг от друга названий для выражения бесконечного множества чисел. Народы, менее подвинувшиеся в счислении, будучи заинтересованы только той узкой его областью, которая определяется обыденными житейскими нуждами, избрали средний путь. Давая независимые друг от друга названия только единицам некоторых разрядов и обозначая другие выражениями, составленными из этих названий на основании законов образования чисел, они достигали не устранения бесконечности независимых друг от друга числительных, а только уменьшения их в области, эксплуатируемой общежитием. Но и это уменьшение достигалось ими в ущерб краткости. В результате, и у индусов, и у народов, избравших средний путь, употребляемые формы решения основного вопроса словесной Н. оказывались удовлетворяющими минимуму его требований; идеал же оставался по-прежнему не достигнутым. Наблюдениям над словесною Н. у разных народов история происхождения и последующего развития счисления обязана главной частью своего материала. В настоящее время, в полном виде или в виде следов и остатков прежнего употребления, 5-ричная система счисления употребляется у 26 племен Африки, 8 — Полинезии, 13 — Азии и 30 — Америки; 20-ричная у 4 племен Африки, 3 — Полинезии, 18 — Азии, 8 — Америки и 6 — Европы. Что же касается 10-ричной системы, то частью вследствие некоторых выгод, доставляемых ее употреблением для словесной и письменной Н., главным же образом вследствие употребления ее народами, стоявшими во главе умственного движения человечества, она сделалась в настоящее время единственно употребляемой во всех цивилизованных обществах, и делаемые в настоящее время предложения ее замены другими будто бы более удобными системами счисления (напр. 12-ричной) едва ли могут быть считаемы вызванными какими-нибудь нуждами дела. Вызванное появлением систем счисления начало употребления письменной Н. (см. Математика) было в то же время и началом употребления письма вообще, как об этом согласно свидетельствуют, с одной стороны, те из современных дикарей, которые, видя впервые процесс письма, обозначают его глаголом "считать", а с другой — те из языков цивилизованных народов, в которых действия письма и счета обозначаются одним и тем же глаголом. Два рода предметов, употребляемых в качестве первых письменных знаков для обозначения основных чисел систем счисления (камни и подобные им предметы и штрихи, проводимые на песке или красящим веществом на какой-нибудь поверхности), направили развитие письменной Н., а вместе с ним и самого письма, по двум путям. Первый из этих путей повел ее от первоначального пользования камнями (латинское calculare — считать от calculus — камешек) к столь распространенному в Китае и у туземных племен Южной Америки, а также и у многих народов Африки и Австралии, употреблению шнурков с узлами, которое, как особая форма письма вообще, достигло своего наивысшего развития в перуанском квипусе. Первыми формами, усвоенными письменной Н. при следовании по второму пути, были бирка и системы знаков живописного письма. Затем вместе с самим письмом письменная Н. прошла и через все последующие стадии его развития, представляемые иероглифическим письмом, иератическим, клинообразным и, наконец, звуковым. Из трех форм, в которых представляется или может быть представлено письмо в настоящее время, словесной, звуковой и идейной (Begriffsschrift), письменная Н. с очень раннего времени примкнула к идейной, то есть именно к той, которая для письма вообще представляет еще его будущую форму, как это можно видеть из самого понятия идейного письма, знаки которого должны быть символами основных элементарных понятий, соединяемыми для выражения сложных, на основании законов, управляющих образованием последних из первых в действительности. Своим ранним переходом к этой высшей будущей форме письма письменная Н. обязана простоте содержания счисления. В то время как в других областях человеческого знания числа основных элементарных понятий, а также и родов их сочетания, говоря вообще, весьма значительны, в области счисления основное элементарное понятие только одно — понятие способной к повторению в каком угодно числе раз единицы; родов же сочетания, известных под именем основных арифметических действий, не более четырех (даже можно считать двух). Идеал письменной Н., как одного из частных случаев идейного письма, состоит в самом кратком и ясном, с помощью возможно меньшего количества произвольных знаков, выражении всякого числа по его понятию, то есть по его образованию в системе счисления. В бессознательном стремлении к этому идеалу человечество в разные эпохи и в лице разных народов изобрело множество более или менее различающихся между собой систем числовых знаков, или цифирных систем, если называть числовые знаки вообще цифрами. Все эти системы в сущности суть только более или менее удачные попытки решения следующих двух основных вопросов развития письменной Н.: как выразить разряды системы счисления? как представить кратные единиц этих разрядов? Первоначальным решением этих вопросов, доставленным естественными ходом развития, было для первого — обозначение единиц разрядов особыми знаками и для второго — помещение этих знаков рядом в требуемом количестве, меньшем, чем основное число системы, или так называемый аддитивный метод. Как естественные, вполне выражающие в своей области образование сложных понятий из элементарного, эти решения принимали участие в образовании всех последующих цифирных систем, носящих на себе тем более заметные следы деятельности человеческого разума, чем к более позднему времени они принадлежали. Обозначение единиц разрядов особыми знаками удерживалось почти до самого конца развития письменной Н. Аддитивный же метод, рассматриваемый в смысле выражаемого им общего принципа и потому не ограничиваемый одним выражением кратных единицам разрядов, составляет основную схему изображения числа во всякой цифирной системе, не исключая и той, которая закончила собой развитие письменной Н. Проникающий, по сказанному, все цифирные системы, аддитивный принцип не определял, однако, порядок размещения разрядов в изображении чисел, который был для него совершенно безразличным. Не таковым, однако же, оказался этот порядок для умственной природы человека, установившей во всех без исключения известных нам цифирных системах один и тот же общий принцип следования меньших разрядов за большими в направлении письма. Значительность количества знаков, требуемых аддитивным методом для выражения кратных единицам разрядов, повела к многочисленным попыткам изыскания средств ее устранения. Одни из этих попыток не получили дальнейшего развития и представляются теперь только в виде следов употребления представляемых ими методов (вычитающий метод римлян, делительный — ацтеков). Напротив, другие развивались и в виде обработанных вполне или отчасти методов получали более или менее значительное распространение. Из них ближайшим по идее к аддитивному методу и в то же время древнейшим был мультипликативный метод, состоящий в выражении кратного единицы какого-нибудь разряда в виде произведения этой единицы на соответствующее число разряда единиц. Знак этого последнего числа, для отличия от его употребления в значении слагаемого, всегда помещается относительно знака единицы разряда со стороны, противоположной направлению письма. Давая возможность выразить всякое кратное единицы какого-нибудь разряда только двумя знаками, мультипликативный метод делает значительный шаг вперед в сравнении с аддитивным методом. Встречаемым им на практике препятствием к полному осуществлению своей цели является многозначие в изображениях как единиц разрядов, так и чисел разряда единиц. В тех же случаях, когда те и другие изображаются независимыми друг от друга одиночными знаками, он достигает высшей доступной для него степени совершенства. Следующим по времени своего наибольшего развития и также достигавшим своей ближайшей цели вполне был метод обозначения кратных единицам разрядов особыми независимыми друг от друга знаками. Требуя для изображения кратного единицы разряда только один знак, этот метод идет далее мультипликативного, но в то же время значительно увеличивая общее число употребляемых в счислении знаков, он крайне затрудняет память. Это последнее обстоятельство делало невозможным сколько-нибудь значительное развитие рассматриваемого метода до самого того времени, когда в распоряжении человечества появился в виде алфавита ряд знаков, имеющих строго определенные порядок и значение. С этого времени метод получил очень широкое распространение, значительно превосходящее распространение мультипликативного метода. Ограниченность числа знаков, составляющих алфавит, делало его непосредственно применимым только к сравнительно очень небольшой области счисления, хотя в практике и особенно употребительной. Стремление к удержанию знаков алфавита и представляемых ими выгод и за пределами их непосредственного приложения к счислению выразилось на практике двумя важными последствиями. Чтобы вторично применить знаки алфавита или буквы к обозначению кратных единицам разрядов, следующих за теми, которые уже получили такое обозначение, пользующиеся ими народы прибавляли к буквам особый значок, напр. помещаемый снизу или сверху штрих или точку. Этот прием, делая, очевидно, безграничным приложение алфавита в методе обозначения особыми знаками, являлся в то же время первоначальной формой нового метода, который может быть назван указательным, как выражающий кратное единицы какого-нибудь разряда присоединением знака этой единицы в виде указателя к знаку соответствующего числа разряда единиц. Вторым последствием упомянутого выше стремления было появление в методе обозначения особыми знаками, а вместе с ним, и в указательном методе, идеи значения числового знака по занимаемому им месту, или, короче, идеи положения. Когда в изображении числа за первым употреблением знаков алфавита следовало второе, тогда не было никакой надобности в удержании указателей, так как вторичное числовое значение букв указывалось самим их местом. И действительно, во всех этих случаях значки указателей употребляющими их народами опускались. Употребление составленных по мультипликативному, или указательному, методу цифирных систем в письменном счете имело своим следствием образование нового метода выражения кратных единицам разрядов. При сложении, напр., большого количества многозначных чисел самый процесс совершения действий по разрядам приводил к помещению слагаемых одного под другим так, чтобы числа одного и того же разряда составляли один столбец. Отсюда было уже недалеко до мысли заменить для сокращения письма повторение в виде множителя или указателя знака единицы разряда при каждом из ее чисел помещением этого знака всего только один раз над принадлежащим ему столбцом. Для большей ясности и предупреждения возможных смешений чисел следующих друг за другом разрядов пришлось отделить упомянутые столбцы один от другого вертикальными линиями. Таким образом, постепенно сформировался новый метод столбцов, состоящий в изображении всякого числа помощью помещения чисел единиц составляющих его разрядов в разграфленных столбцах, над которыми в последовательном порядке и без всяких пропусков писались знаки единиц разрядов. Нетрудно видеть, однако же, что в этих знаках не было никакой существенной надобности, так как разряд, представляемый каким-нибудь из столбцов, определялся местом последнего в среде других. Таким образом, знаки единиц разрядов делались излишними, и на смену им выступало занимаемое разрядом в числе место, другими словами, идея положения впервые получала ясное и полное выражение. Вместе с тем, метод столбцов своими пробелами в изображениях чисел, не содержащих всех обнимаемых ими разрядов, ясно показывал, что для приложения этой идеи к практике необходимо обозначать каким-нибудь способом, пробелом или особым знаком, отсутствие в изображаемом числе того или другого из обнимаемых им разрядов, следствием чего и могло быть принадлежащее индусам введение нуля. Изобретение этого нового знака письменной нумерации дало индусам возможность ввести во всеобщее употребление представляемый идеей положения новый метод выражения кратных единицам разрядов, который поэтому и назыв. методом положения. Выразив с помощью знаков чисел, меньших основного числа употребляемой системы счисления, и нуля все числа уходящего в бесконечность их ряда, этот метод вполне осуществил идеал письменной нумерации и тем закончил развитие последней. От индусов этот метод вместе с характерной системой так назыв. "пыльных" цифр перешел к арабам, а от них в Зап. Европу, через посредство которой распространился и во всем цивилизованном человечестве.
Подробности см. в "Лекциях истории математики" В. В. Бобынина ("Физико-математические Науки", т. IХ и Х, лекции 2 — 6); его же, "Исследования по истории математики" (вып. II, М., 1896).
В. В. Бобынин.
| "БРОКГАУЗ И ЕФРОН" >> "Н" >> "НУ" |
Статья про "Нумерация" в словаре Брокгауза и Ефрона была прочитана 1605 раз
| Бургер двойного помола |
| Жаренный морской черенок |
TOP 15
- Волос
- Проно
- Степные животные
- Гимнастика
- Индийский океан
- Архитектура
- Сравнение, в литературе
- Манда
- Клитры
- Колесование
- Испарение
- Травоядные животные
- Оплодотворение у pacтений
- Вредные насекомые
- Электризация тел