


БНБ
"БРОКГАУЗ И ЕФРОН" (121188)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Начертательная геометрия
Определение "Начертательная геометрия" в словаре Брокгауза и Ефрона
Начертательная геометрия
Начертательная геометрия*
— наука, изучающая пространственные фигуры при помощи их проектирования (проложения) перпендикулярами на некоторые две плоскости, которые рассматриваются затем совмещенными одна с другой. При обыкновенном способе изображения предметов линии, распространяющиеся вдаль от глаза наблюдателя, хотя и изображаются, соответственно с тем, какими они нам представляются, сокращенными, но это сокращение определяется рисовальщиком обыкновенно на глазомер, а фотографией оно хотя в известных случаях и достаточно точно может быть передано, но отношение, в каком потерпели сокращения разные линии изображаемого предмета, остается трудно определимым; вдобавок, во многих случаях и фотография (см.) ведет к перспективным ошибкам. Всякий мастер, будет ли то плотник, слесарь, токарь, камнетес и т. д., может только в том случае выполнить заказанный предмет согласно желанию заказчика, если ему будет дан или совершенно такой же предмет на образец, или модель его, или конструкторский чертеж, по которому легко и точно определялись бы размеры всех начерченных линий, хотя бы и таких, которые удаляются в глубь картины и потому изображаются сокращенными. Н. геометрия учит изготовлению таких чертежей, в которых предмет изображается почти таким, как мы его видим, и притом так, что по начерченным линиям можно в точности определить размеры и истинный вид изображаемого.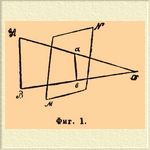
Фиг. 1.
Представим себе, что в точке O (фиг. 1) находится глаз человека, смотрящего на предмет AB. Вообразим между глазом и предметом плоскость MN, расположенную перпендикулярно к той линии, по которой глаз смотрит. Проведем из O прямые к тем точкам предмета, которые характеризуют его форму. Эти прямые, называемые проекционными лучами, пересекут плоскость MN в различных точках. Совокупность таких точек ab и составит картину предмета AB, служащую его изображением. Поэтому плоскость MN и называется плоскостью картины. Точка пересечения проекционного луча и плоскости картины называется центральной проекцией или перспективой той точки предмета, из которой исходит данный проекционный луч. Такой способ изображения предмета называется перспективой. Если вместо того, чтобы проводить проекционные лучи от точек предмета к глазу, мы будем опускать перпендикуляры из точек предмета на плоскость картины, то полученное изображение, представляемое совокупностью оснований этих перпендикуляров, будет сохранять некоторое сходство с перспективным. Действительно, чем больше точка O будет удалена от предмета, тем больше проекционные лучи будут приближаться к положению взаимно параллельному и перпендикулярному к плоскости картины. Такое изображение называется ортогональной проекцией. Итак, в ортогональной проекции каждая точка предмета изображается основанием перпендикуляра, опущенного из неё на плоскость картины. Получение, по данному чертежу, истинных размеров и другие построения несравненно проще выполняются при ортогональном проектировании, чем при перспективе (см. Перспектива).
Основная идея Н. геометрии заключается в следующем: если имеются две ортогональные проекции предмета на две плоскости, различным образом относительно предмета расположенные, то, с помощью сравнительно несложных построений над этими двумя изображениями, можно получить истинные размеры предмета, истинный вид его плоских линий и ортогональную проекцию на любую заданную третью плоскость. Конечно, для этого необходимо нужно знать, в каком масштабе были даны заданные две ортогональные проекции, т. е. в каком общем отношении весь чертеж был уменьшен или увеличен против действительности. Обыкновенно задают вид предмета его ортогональными проекциями на такие две плоскости, из которых одна горизонтальна и называется планом, а другая вертикальна и называется фасадом. Их также называют горизонтальной и вертикальной плоскостями проекции. Ортогональная проекция предмета на плоскость, перпендикулярную к плану и фасаду, называется боковым видом. Весьма важный прием Н. геометрии заключается в том, что плоскость фасада, бокового вида и всякие другие плоскости, на которые проектируется предмет, мысленно отгибают на плоскость плана поворотом около прямой, по которой план пересекается с отгибаемой плоскостью. Этот прием называется совмещением. Дальнейшие построения совершаются уже на таком совмещенном чертеже, как это указано ниже. Так как всякий предмет представляет собой совокупность точек, то прежде всего необходимо познакомиться с изображением плана и фасада точки на совмещенном чертеже.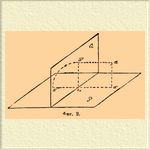
Фиг. 2.
Пусть a (фиг. 2) будет данная точка; P плоскость плана; Q плоскость фасада. Опустив из a перпендикуляр на план, получим план a' точки a; опустив из a перпендикуляр на фасад, получим фасад b точки a. Перпендикуляры aa' и ab называются проектирующими линиями. Плоскость bаa', определяемая проектирующими линиями, называется проектирующей плоскостью. Она перпендикулярна как к плану, так и к фасаду и, следовательно, перпендикулярна к пересечению плоскости плана и фасада, называемому общим прорезом. Пусть a о есть та точка, в которой проектирующая плоскость пересекается с общим прорезом: a о a' и aob будут перпендикулярны к общему прорезу. При данных плоскостях плана и фасада положение точки a вполне определяется ее планом a' и фасадом b, так как a находится на пересечении перпендикуляра, восставленного из a' к плоскости плана, с перпендикуляром, восставленным из b к плоскости фасада. Для получения совмещенного чертежа повернем плоскость Q фасада в направлении, указанном стрелкой, около общего прореза до совпадения с плоскостью плана. При этом точка b упадет в a". Таким образом точка a", представляющая собой совмещенный фасад точки a, будет лежать на продолжении перпендикуляра a'ao, опущенного из плана a' на общий прорез. Таким образом получится совмещенный чертеж, изображенный на фиг. 3, где MN есть общий прорез; a' — план и a" — совмещенный фасад точки a, которая сама уже не изображается.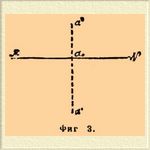
Фиг. 3.
Н. геометрия имеет дело только с совмещенными чертежами; каждая точка дается планом и совмещенным фасадом; к чертежам же, исполненным обыкновенными приемами (каковы у нас фиг. 1, 2 и 5), прибегают только в начале изучения этой науки.
Проекция прямой. Прямая определяется двумя точками. Следовательно, если имеется план и фасад (совмещенный) двух точек a и b, лежащих на прямой, то прямая a'b', соединяющая планы точек a и b, будет планом прямой ab и прямая a"b", соединяющая фасады точек a и b, будет фасадом прямой ab. На чертеже 4 изображена прямая ab своими планом и фасадом.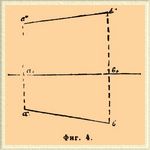
Фиг. 4.
Определение истинной длины прямолинейного отрезка, заданного планом и фасадом. Воспользуемся чертежом, исполненным обыкновенным способом (фиг. 5).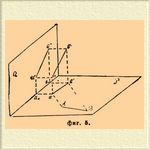
Фиг. 5.
Пусть ab есть данный прямолинейный отрезок, a'b' его план a"b" его фасад. Повернем плоскость a'abb' около прямой a'b' и отогнем ее в положение a'b'BA на плоскость плана. При этом отрезок ab примет положение AB. Следовательно:
Aа' = aa' = a"ao
Bb' = bb' = b"bo
Перпендикулярность прямых a'a и b'b к a'b' не изменилась, следовательно, чтобы по данному плану и фасаду прямолинейного отрезка на совмещенном чертеже (фиг. 6) определить истинную его длину, нужно: восставить из a' и b' к плану a'b' перпендикуляры и на них отложить: a'A=aoa"; b'B=bob".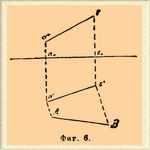
Фиг. 6.
Прямая AB и будет равна истинной длине прямой ab. На этом примере и видим, что на чертеже 5, исполненном обыкновенным способом, прямая ab изображена в укороченном виде соответственно тому, как мы ее видим, и так как степень этого укорочения неизвестна, то по чертежу 5 нельзя определить истинного расстояния ab. Между тем на чертеже 6, хотя сама прямая ab и не изображена, а даны только ее план a'b' и фасад a"b", то по ним можно совершенно точно определить представляемую ими прямую.
Определение бокового вида точки по данным ее плану u фасаду. Пусть a' есть план и a" фасад заданной точки (фиг. 7), плоскость же бокового вида пересекает плоскость плана по прямой on и плоскость фасада по прямой om.
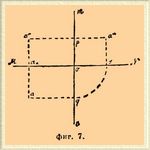
Фиг. 7.
При совмещении плоскостей плана и фасада om и on окажутся лежащими на одной прямой mn, перпендикулярной к MN, так как мы предполагаем, что плоскость бокового вида перпендикулярна к плоскостям плана и фасада. Совмещение трех плоскостей предполагаем происшедшим следующим образом: сначала плоскость бокового вида была совмещена вращением около om с плоскостью фасада; затем они обе вращением около MN были совмещены с плоскостью плана, которая и представляет собой плоскость чертежа. Не трудно видеть, что при этом расстояние a"s бокового вида a"' точки a от MN будет равно a о a" и расстояние а'" от om будет равно aoa'. Отсюда получаем такое построение: когда заданы a' и a", то проводим к MN перпендикуляр mn и на него опускаем перпендикуляр a'q из a'; радиусом oq описываем из центра o дугу, которая пересечет MN в точке s; из s восставляем перпендикуляр к MN. Пересечение этого перпендикуляра с прямой, проведенной через фасад a" параллельно MN, и будет боковым видом a'".
Определение бокового вида многоугольника. Если даны (фиг. 8) план и фасад сторон многоугольника, а следовательно, и его вершин, то, строя боковые виды вершин, получим и боковой вид многоугольника. При множестве точек, с которыми имеем дело на чертеже, удобно их обозначать цифрами.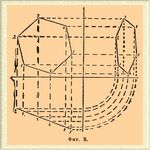
Фиг. 8.
Проектирование параллелепипеда. Обыкновенно задаются таким положением плоскостей плана и фасада, при котором данный предмет проектируется на них простым чертежом и уже по этому плану и фасаду строят проекцию предмета на такую плоскость, на которой он изображается во всей своей сложности. Первоначальные план и фасад можно даже так выбрать, чтобы на них не искажались некоторые размеры предмета. Покажем это на следующем примере изображения параллелепипеда (фиг. 9).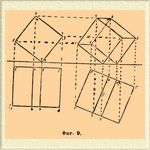
Фиг. 9.
Представим себе, что параллелепипед лежит одним из своих ребер на плоскости плана, а заднее и переднее его основания параллельны плоскости фасада. Тогда эти основания проектируются на фасад, налагаясь одно на другое (заслоняя одно другое), но в истинном виде. На плане получается проекция, в которой сохраняется величина ребер, параллельных плану. Повернем мысленно параллелепипед около некоторой вертикали и отнесем его несколько в сторону. Тогда и план его повернется на тот же угол и отнесется в сторону. Чтобы получить план нового положения, проводим прямую 1'3', составляющую некоторый угол с направлением 1 3 прежнего плана, и на этой прямой строим приемами обыкновенной геометрии фигуру, равную прежнему плану. Вершины фасада нового положения будут лежать на перпендикулярах, опущенных из вершин нового плана на общий прорез. Кроме того, они будут лежать на параллелях, проведенных из вершин прежнего фасада к общему прорезу, потому что при сказанном перемещении параллелепипеда его вершины остались на прежней высоте от плоскости плана. Итак, пересечения упомянутых перпендикуляров и параллелей и будут вершинами нового фасада. Соединяя их между собой и изображая более слабыми чертами линии, заслоненные параллелепипедом, получим такое его изображение, в котором видны уже все его 12 ребер. Как для изображения параллелепипеда достаточно изобразить его ребра, так и для изображения кривой поверхности достаточно изобразить ее наиболее характеристичные линии, между которыми первенствующее значение имеет видимый контур — кривая, по которой проектирующие линии касаются поверхности.
Пересечение двух круглых цилиндров. Для уяснения способа изображения кривых поверхностей рассмотрим применение Н. геометрии к следующему практическому вопросу. Требуется соединить между собой две трубы, склепанные из котельного листового железа, так, чтобы одна труба, будучи перпендикулярна другой, врезалась бы в нее более чем на половину своей толщины. Для этого в одной из труб (положим, в большей) должно быть проделано окошко, которое удобнее, конечно, проделать в листе, из которого делается большая труба, пока она еще не склепана. Требуется определить форму того окошка, которое должно быть прорезано в листе, служащем для приготовления большой трубы.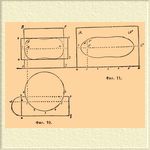
Фиг. 10. Фиг. 11.
Пусть (фиг. 10) плоскость плана будет перпендикулярна к большой трубе, а плоскость фасада параллельна осям обеих труб. Тогда план большой трубы будет окружность 036 и фасад ее изобразится прямоугольником ABCD. План малой трубы будет mnpq и фасад abcd. Пусть HF будет фасад диаметральной и параллельной плану плоскости малой трубы. На nm, как на диаметре, опишем дугу nsm. Зададимся какой-нибудь образующей h5 малой трубы и определим фасад той точки взаимного пересечения труб, которая лежит на этой образующей и план которой есть, следовательно, точка 1. Искомый фасад точки, во-первых, должен лежать на перпендикуляре, опущенном на общий прорез из точки 1. Во-вторых, он будет лежать от HF на высоте HS, равной hs. Итак, точка S есть искомый фасад. Задаваясь другими образующими и строя фасады точек взаимного пересечения труб, получают целый ряд точек, соединением которых получится фасад пересечения труб. Теперь развернем полуокружность 036. Задача эта (см. Квадратура) может быть исполнена только приближенно. Она решается с достаточным приближением, если принять длину полуокружности за сумму стороны вписанного квадрата и стороны правильного вписанного треугольника. Сторона вписанного квадрата будет хорда 36, сторона треугольника есть хорда 04, если цифры обозначают деления полуокружности на 6 частей. Сумму этих хорд откладывают на особом чертеже (фиг. 11) и делят ее на 6 частей. Пусть PQ будет соответствовать упомянутой диаметральной плоскости малой трубы: она должна быть проведена параллельно прямой 012... на расстоянии OP=AE. Восставляя из деления 1 перпендикуляр к прямой 012... и откладывая на нем от пересечения его с PQ величину h's'=hs=HS, получим точку s' той искомой кривой, по которой должно быть вырезано в листе MN окошко. Получая таким же путем другие точки искомой кривой, определим и самую эту кривую, изображенную на чертеже (фиг. 11).
Н. геометрия создана была в конце прошлого столетия Монжем (см.). Она имеет тесное отношение к теории теней (см. Тени) и к способу аксонометрических проекций (см. Проекции). Лучшими руководствами по Н. геометрии могут служить руководства: Макарова, Сомова, Monge, Leroy и проч.
Н. Делоне.
| "БРОКГАУЗ И ЕФРОН" >> "Н" >> "НА" >> "НАЧ" |
Статья про "Начертательная геометрия" в словаре Брокгауза и Ефрона была прочитана 1557 раз
| Коптим скумбрию в коробке |
| Ананасы на гриле |
TOP 15
- Волос
- Проно
- Степные животные
- Гимнастика
- Индийский океан
- Архитектура
- Сравнение, в литературе
- Манда
- Клитры
- Колесование
- Испарение
- Травоядные животные
- Оплодотворение у pacтений
- Вредные насекомые
- Электризация тел