


БНБ
"БРОКГАУЗ И ЕФРОН" (121188)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Направляющие механизмы
Определение "Направляющие механизмы" в словаре Брокгауза и Ефрона
Направляющие механизмы
Направляющие механизмы*
— Этим именем называются механизмы, в которых, при движении одной точки по окружности или по дуге окружности, некоторая другая точка движется по прямой. Задача об изыскании Н. механизмов была установлена Ваттом, который, усовершенствуя паровую машину, встретился с необходимостью передать прямолинейное движение головки поршневого штока концу коромысла, который движется по дуге окружности. В настоящее время паровые машины устраиваются без коромысла; головка поршневого штока удерживается на прямой линии салазками, и это прямолинейное движение преобразуется во вращательное движение махового колеса просто шатуном. Тем не менее продолжавшаяся почти в течение века погоня за изобретением наиболее совершенного Н. механизма имела громадное значение в истории развития теории механизмов; исследования, сделанные в этом направлении, внесли яркий свет в понимание законов передачи движения. Н. механизмы подразделяются на точные и приближенные. Точные должны, теоретически говоря, вести точку строго прямолинейно.
В настоящее время известны следующие точные Н. механизмы, в которых неподвижные шарниры обозначены точками, обведенными окружностями:
1) антипараллелограмм Гарта (фиг. 1) преобразует движение точки M по окружности в движение точки G по прямой.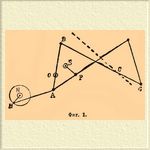
Фиг. 1.
В нем AB=CD; BC=AD; SP=SO, стержни, изображенные толстыми линиями, соединены между собой в указанных крупными точками местах шарнирами. Шарниры O, S, H неподвижны. Длина кривошипа НМ и шатуна MA произвольна, лишь бы при вращении стержня HM точка A колебалась по дуге описанной из O радиусом OA. Положения точек P и G определяются как пересечения стержней AD и BC с прямой OG, проведенной параллельно BD из произвольно взятой на AB точки O. Этот механизм видоизменен много в следующий (фиг. 2), к которому можно присоединить также шатун и кривошип, не изображенные на фиг. 2.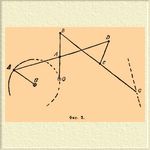
Фиг. 2.
Здесь движение точки G не заслоняется частями механизма.
2) Прямило Гарта (фиг. 3). В нем точка P ходит по прямой AP, точка Q по прямой AQ; любая точка стержня BC или его продолжения может быть соединена с шатуном, соединенным с вращающимся кривошипом, которые и не изображены.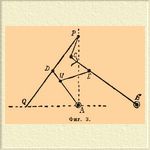
Фиг. 3.
Должны быть соблюдены равенства AD=DP; AH=HE; EC=CP; DQ=DP и условие АН<AB. В этом механизме концы стержня PQ ходят по прямым и потому (см. Механизм) все точки стержня PQ, кроме Q, D и P, чертят эллипсы. Шарниры A и B неподвижны.
3) Положительный инверсор Посселье (фиг. 4). В нем АВ=ВС=CD =AD; OB=OD; PA=OP, шарниры O и P неподвижны; точка C чертит перпендикулярную к OP прямую. Замечательное свойство соединения ромба АВСD со стержнями OB и OD заключается в том, что в таком соединении величина произведения ОА ∙ ОС постоянно остается равным OB2—BC2.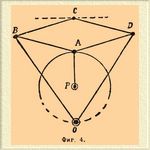
Фиг. 4.
4) Отрицательный инверсор Посселье (фиг. 5). В нем C чертит перпендикулярную к PO прямую; шарниры O и P неподвижны; АВ=ВС=CD=AD; ОР=АР. Произведение AO∙OC остается постоянно равным BC2—OB2.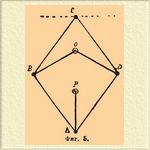
Фиг. 5.
5) Механизм Брикара (фиг. 6). Построим квадрат ABCD и его диагонали AC и BD. Середины сторон AD и BC разделим пополам в точках Е и F. Стержни AD, AC, BC, ВО и DO соединим шарниром в точках A, В, C, D, E, О и устроим в точках Е и F неподвижные шарниры. Таким образом диагональ DB будет составная из равных между собой стержней DO и OB, диагональ же АС представляет собой целый стержень. Точка O соединения стержней OB и OD описывает прямую, перпендикулярную к EF. На чертеже O отодвинуто в сторону, чтобы показать, что диагональ АС не составная.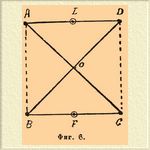
Фиг. 6
Приближенные Н. механизмы ведут точку по кривой, некоторая часть которой весьма мало уклоняется от прямой; на протяжении же этой части уклонение от прямолинейного движения настолько мало, что на практике приближенные Н. механизмы не уступают точным. Таких механизмов изобретено великое множество. Из них наиболее известны:
1) параллелограмм Ватта (фиг. 7), ведущий точки p, n и m по прямым.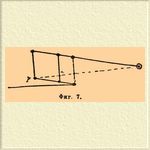
Фиг. 7.
2) Прямило Чебышева (фиг. 8), ведущее точку B приблизительно по прямой при движении точки A по дуге α A β. Этот механизм замечательно мало отклоняет точку B от прямолинейного движения. Условия: ОС=АС = ВС =64; OD=25; AD= 11. Стержень АСВ не сгибается в точке C; шарниры O и D неподвижны.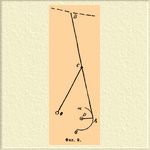
Фиг. 8.
3) Непрерывный трансформатор Чебышева. Замечательнейший из всех Н. механизмов, потому что, состоя только из трех подвижных частей, не нуждается, для преобразования непрерывного вращения (а не колебания только) в прямолинейное движение, в прибавлении кривошипа и шатуна, так как в этом замечательном механизме непрерывное вращение стержня DA около точки D непосредственно преобразуется в поступательное движение точки B, весьма мало уклоняющееся от прямолинейного и совершающееся взад и вперед. Механизм состоит из прямоугольного треугольника АСВ (который может быть заменен стержнем, согнутым в точке C под прямым углом) с равными катетами CA и CB, стержня OC, равного CA, и стержня AD. Размеры могут быть следующие: AC=BC=OC=100; OD=141; DA=5.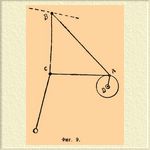
Фиг. 9.
Литература предмета весьма обширна; укажем на следующие сочинения: Чебышев, "О простейшей суставчатой системе, доставляющей движения симметрические около оси" ("Приложение к LX тому Записок Имп. Академии Наук", 1889); Burmester, "Lehrbuch der Kinematik"; Делоне, "Передача вращения и механическое черчение шарнирно-рычажными механизмами". Более полное указание на литературу предмета можно найти в статье Лигина, "Liste des travaux sur les syst èmes articulés" ("Bulletin des scienses Mathé matiques", т. VII); Neuberg, "Sur quelques syst èmes des tiges arliculées"; Kempe, "How to draw a stright line" ("The Natu re", т. XVI).
H. Делоне.
| "БРОКГАУЗ И ЕФРОН" >> "Н" >> "НА" >> "НАП" |
Статья про "Направляющие механизмы" в словаре Брокгауза и Ефрона была прочитана 1539 раз
| Коптим скумбрию в коробке |
| Кукурузный крем суп со скатом |
TOP 15
- Волос
- Проно
- Степные животные
- Гимнастика
- Индийский океан
- Архитектура
- Сравнение, в литературе
- Манда
- Клитры
- Колесование
- Испарение
- Травоядные животные
- Оплодотворение у pacтений
- Вредные насекомые
- Электризация тел