


БНБ
"БРОКГАУЗ И ЕФРОН" (121188)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Наклонная плоскость
Определение "Наклонная плоскость" в словаре Брокгауза и Ефрона
Наклонная плоскость
Наклонная плоскость*
— плоскость, поставленная наклонно к горизонтальному направлению и употребляемая для поднятия тяжестей на высоту. Свойством Н. плоскости облегчать поднятие тяжестей люди пользовались уже с давних пор, но точное изучение сил, действующих на груз, находящийся на Н. плоскости, начато было только в 1586 г. Стевином в его "Трактате о статике". Возьмем твердое тело (фиг. 1), ограниченное сверху двумя плоскостями AB и BC, причем AB короткая и поэтому поднимается круто, плоскость же BC длинная и потому отлогая.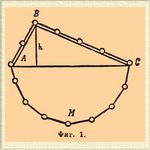
Фиг. 1.
Перекинем через такое тело тяжелую цепь, концы которой связаны один с другим; тогда цепь расположится, как это показано на фиг. 1. Часть цепи AMC можно рассматривать как уравновешенную точно таким образом, как будто она была закреплена в A и C. Остаются части AB и BC, взаимно уравновешивающиеся. Часть AB представляет собой груз во столько раз меньший сравнительно с грузом, представляемым частью BC, во сколько AB меньше BC. Если грузы, пропорциональные сторонам AB и BC, взаимно уравновешиваются, то равные между собой грузы уравновешиваются на Н. плоскостях силами, обратно пропорциональными сторонам AB и BC. Итак, силы, заставляющие груз скользить с Н. плоскости, т. е. действующие параллельно Н. плоскости, при той же высоте h, обратно пропорциональны длине Н. плоскости. Но сила, действующая на груз, прислоненный к вертикальной плоскости, равна весу P груза. Следовательно (фиг. 2), сила Q, действующая на тело, лежащее на Н. плоскости параллельно наклону этой плоскости, относится к весу этого тела как высота h к длине плоскости BC.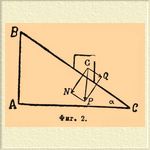
Фиг. 2.
Получается формула Q/P=h/l. Чтобы поднять груз вертикально, нужно преодолеть его вес P. Чтобы втащить груз на ту же высоту по Н. плоскости, нужно преодолеть силу Q, во столько раз меньшую сравнительно с P, во сколько катет h меньше гипотенузы BC. В настоящее время этот закон Н. плоскостей доказывается разложением (фиг. 3) веса тела на две силы, из которых N перпендикулярна в Н. плоскости и вследствие этого только прижимает тело к плоскости; другая же сила Q параллельна наклону плоскости.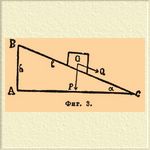
Фиг. 3.
Из прямоугольного треугольника PGQ получается:
Q = P ∙ sin α (1).
Отсюда получается Q/P = AB/BC.
В действительности еще является сила трения, пропорциональная давлению N и равная F=P∙tg φ ∙cos α, где φ есть тот самый угол, до которого надо поднять Н. плоскость, чтобы лежащий на ней груз начал с неё сползать. Этот угол называется углом трения и зависит от того, из каких материалов сделаны Н. плоскость и соприкасающаяся с ней поверхность лежащего на ней груза. Величина tgφ называется коэффициентом трения и дается для различных материалов в особых таблицах (см. Трение). Сила S, потребная для того, чтобы поднять тело по Н. плоскости, должна преодолеть как силу трения, так и силу Q. Поэтому
S = T + Q = (tg φ ∙cos α + sin α)∙P (2).
Силе же M, потребной для того, чтобы совлечь тело вниз по плоскости, будет помогать и сила Q. Следовательно:
M = T — Q = (tg φ ∙cos α — sin α)∙P (3).
Если по этой формуле величина M выйдет отрицательной, то абсолютная величина этого отрицательного количества представит собою силу, потребную для удержания груза на месте так, чтобы он не скользил вниз по плоскости. Применим эти формулы к следующему примеру. Нужно втащить деревянный ящик в 10 пудов весом по деревянной доске, составляющей с горизонтальным направлением угол в 30°; sin 30° = 1/2 и cos 30° составляет около 0,87. Коэффициент tgφ трения дерева по дереву равен 1/2. Вставляя эти величины в формулу (2), получим величину сил S = 9,35 пуда. Для того чтобы определить силу M, потребную для удержания ящика от сползания с этой Н. плоскости, нужно вставить те же величины в формулу (3). Получим М = —0,65 пуда = —26 фунтов. Такая значительная разница между S и М станет понятной, если заметим, что для передвижения ящика по горизонтальной доске требуется сила, вычисляемая по формуле (1) при α = 0 и равная 5 пудам, между тем как для удержания ящика на горизонтальной доске не требуется никакой силы. В истории механики Н. плоскость играла весьма видную роль. Один из крупнейших шагов в этой науке сделан был Ньютоном, когда он открыл всемирное тяготение; этому открытию предшествовало предварительное изучение, еще Галилеем, законов падения тел, для чего он пользовался Н. плоскостью. Изменяя наклон α плоскости, можно заставлять падать (катиться) по ней одно и то же тело под действием различных сил Q, и при этом при малых α тело падает достаточно медленно, чтобы можно было за ним следить. Галилей и применял к изучению падения именно Н. плоскость, но он же изучал законы колебания маятника, служащего лучшим орудием для изучения законов тяготения. Н. плоскость употребляется также для изучения законов трения (см. Трение).
Н. Д.
| "БРОКГАУЗ И ЕФРОН" >> "Н" >> "НА" >> "НАК" |
Статья про "Наклонная плоскость" в словаре Брокгауза и Ефрона была прочитана 3617 раз
| Яйца в кляре |
| Яйца в кляре |
TOP 15
- Волос
- Проно
- Степные животные
- Гимнастика
- Индийский океан
- Архитектура
- Сравнение, в литературе
- Манда
- Клитры
- Колесование
- Испарение
- Травоядные животные
- Оплодотворение у pacтений
- Вредные насекомые
- Электризация тел