


БНБ
"БРОКГАУЗ И ЕФРОН" (121188)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Наибольшие и наименьшие показатели
Определение "Наибольшие и наименьшие показатели" в словаре Брокгауза и Ефрона
Наибольшие и наименьшие показатели — Способ Н. и наименьших показателей был предложен Ньютоном для разложения переменного у в ряд по убывающим или по возрастающим степеням переменного х в тех случаях, когда х и у связаны уравнением вида f(x,y) = 0. Способ этот, называемый также параллелограммом Ньютона, может иметь широкое применение к теории алгебраических функций, к исследованию особых точек кривых, к теории дифференциальных уравнений и так далее. Пусть данное уравнение будет: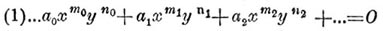
Цель рассматриваемого способа заключается в отыскании разложения переменного у по степеням переменного x, т. е. в нахождении для разложения:
y = Ax α + By β + Cy γ
показателей: α, β, γ ... и коэффициентов: А, В, С... Положим, что требуется найти разложение по восходящим степеням, т. е. что: α < β < γ... Вставив в данное уравнение (1) вместо у величину Ax α получим: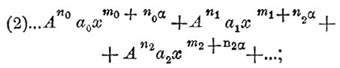
если α наименьший показатель в искомом разложении, то (по Ньютону) среди величин:
(3)... m0 + m0 α; m1 + m1 α; m2 + m2 α ...
найдутся по крайней мере две, которые будут равны между собой и меньше остальных величин ряда (3). В силу этого принципа задача о нахождении α сводится к тому, чтобы составить всевозможные равенства из величин ряда (3), приравнивая их одну другой, из полученных уравнений определить различные значения α и из этих значений выбрать такие, которые обращали бы соответственные равные величины ряда (3) в наименьшие. Выбранные таким порядком значения и будут наименьшими показателями разложения. Сколько определится наименьших показателей, столько будет и разложений, удовлетворяющих вопросу. Для определения коэффициента А, вставим один из найденных наименьших показателей вместо α в уравнение (2) и приравняем нулю сумму коэффициентов тех членов этого уравнения, которые окажутся содержащими одинаковые степени переменного x. Таким образом получим уравнение, из которого определится А. Найдя α и А, полагаем:
у = Ах α + y1
Вставляя эту величину переменного у в данное уравнение (1), получим уравнение вида F(x,y1) = 0, с которым поступаем так, как до сих пор поступали с данным уравнением, причем найдем второй член Вх β искомого разложения. Однако, здесь мы выбираем только тех показателей переменного х в разложении у, которые, удовлетворяя началу наименьших показателей, будут более найденного α. Затем, полагая
у 1 = Вх βу 11
преобразуем уравнение F(y,x1) = 0 в уравнение F1 (x,у 11) = 0 и продолжаем вычисление для определения Cy γ и дальнейших членов разложения. Для нахождения таких значений α, при которых некоторые из величин ряда (3) вышли бы равными между собой и меньшими остальных, служит табличка (см. ниже). Пусть дано уравнение:
(1)'... x2y3 — 3x3y2 — 3y2 + xy + x4 + 1 = 0
Вставляя в него вместо у величину Ах, получим:
(2)'... A3 х 3 α + 2 — 3A2x2 α +3 — A2x2 α + Ax α + 1 + 1 = 0
Показатель 2 α + 3 второго члена уравнения (2) не следует принимать в рассмотрение, потому что он при всяких α более показателя 2 α третьего члена. Ряд, соответственный ряду (3) изложенной выше теории, будет:
(3)'... 3 α + 2; 2 α; α + 1; 0.
Найдя всевозможные уравнения, составленные из этих величин, как то:
3 α + 2 = 2 α;
3 α + 2 = α + 1
и проч. и вставляя в ряд (3) определенные из этих уравнений значения α, составляем табличку:
| Величины ряда (3)' | I | II | III | IV | V | VI |
| = — 2 | α = —1/2 | α = —2/3 | α = + 1 | α = 0 | α = — 1 | |
| 3 α + 2 | — 4 | + 1/2 | 0 | 5 | 2 | + 1 |
| 2 α | — 4 | — 1 | — 4/3 | 2 | 0 | — 2 |
| α + 1 | — 1 | 1/2 | 1/3 | 2 | 1 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Началу наименьших показателей удовлетворяет только α = — 2 и α = 0, потому что только в 1-м и V-м столбцах мы находим величины, равные между собой и меньшие сравнительно с другими величинами своего столбца; именно в 1-м столбце число — 4 стоит против 3 α + 2 и против 2 α, в V-м столбце число 0 стоит против 2 α и против 0. Напр. IV столбец и соответственная ему величина α = + 1 не годятся, потому что, хотя в этом столбце число 2 встречается два раза, но в нем же есть число 0, которое меньше чем 2. Итак, возможны два допущения для первого члена искомого разложения: А 1 х — 2 и А 2 х 0. Для определения А 1 замечаем, что при подстановке — 2 вместо α в уравнение (2)' окажутся равными показатели членов: A3 х 3 α + 2 и A2x2 α . Приравнивая сумму их коэффициентов нулю, получим: А 3 — А 2 = 0, откуда А 1 = 1. Точно так же найдем (из подстановки числа 0 вместо α), что А 2 = ± 1. Итак, получим три разложения:
у = x — 2 +...
у = + 1 +...
y = — 1 +...
Указанным в приведенной выше теории порядком найдем и остальных членов этих разложений. Остановимся, напр., на первом разложении. Первый член его мы нашли равным x— 2. Чтобы найти следующий член, полагаем: у = x — 2 + y1. Вставив эту величину у в данное уравнение, получим:
x2(x— 2 + y1)3 — (3x3 + 1) (x— 2 + y1)2 + x(x— 2 + y1) + x4 + 1 = 0
поступая с полученным уравнением подобно тому, как поступали с данным, определим В и β и так далее. В получаемом таким путем разложении по восходящим степеням переменного х можно пренебрегать высшими степенями этого переменного, если х небольшая величина. Если же х величина большая, то можно пренебрегать его малыми степенями, а потому в этом случае удобнее стремиться найти разложение у по нисходящим степеням переменного х. В этом случае прибегают к способу Н. показателей, совершенно сходному со способом показателей наименьших. Рассматриваемый способ был дан Ньютоном в знаменитом его сочинении: "Methodus fluxionum et serierum infinitarum cum ejusdem applicatione ad curvarum geometriam". Затем этот способ положен основанием изучения алгебраических кривых в сочинении Крамера: "Introduction à l'analyse des lignes courbes algebriques" (1750). Лиувилль применил этот способ к вычислению некоторых симметрических функций: "Jonrnal des Math ématiques pures et appliqué es" (т. VI). Пюизе прилагал этот способ к теории алгебраических функции, Бугаев — к теории дифференциальных уравнений: "Математический Сборник" (т. XVI). Геометрическое построение, соответствующее этому способу, изложено в "Аналитической Геометрии" Д. А. Граве. В аналитической форме способ Н. и наименьших показателей изложен у Serret в его "Cours d'alg è bre superieure" (т. II) и у Бугаева в его ст.: "Различные приложения начала Н. и наименьших показателей к теории алгебраических функций" ("Матем. Сборник", т. XIV).
Н. Д.
| "БРОКГАУЗ И ЕФРОН" >> "Н" >> "НА" >> "НАИ" |
Статья про "Наибольшие и наименьшие показатели" в словаре Брокгауза и Ефрона была прочитана 1464 раз
| Гороховое пюре |
| Гороховое пюре |
TOP 15
- Волос
- Проно
- Степные животные
- Гимнастика
- Индийский океан
- Архитектура
- Сравнение, в литературе
- Манда
- Клитры
- Колесование
- Испарение
- Травоядные животные
- Оплодотворение у pacтений
- Вредные насекомые
- Электризация тел