


БНБ
"БРОКГАУЗ И ЕФРОН" (121188)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Момент инерции
Определение "Момент инерции" в словаре Брокгауза и Ефрона
Момент инерции (Moment d'inertie, Trä gheitsmoment, Moment of inertia) — понятие это введено в науку Эйлером, хотя уже Гюйгенс раньше пользовался выражением того же рода, не давая ему особого названия: один из путей, приводящий к его определению, следующий. Положим, что каждая частица системы имеет массу т и все они движутся прямолинейно, со скоростью v, общей для всех частиц как по величине, так и по направлению; тогда живая сила W такой системы выразится уравнением:
W = 1/2∑mv2 = 1/2Mv2,
так как сумма масс всех частиц системы равна М, массе всей системы. Когда же твердое тело или вообще неизменяемая система вращается около неподвижной оси, дело сложнее: одна угловая скорость, w, будет общая для всех частичек системы, линейные же скорости каждой из них будут иметь мерой произведение ее кратчайшего расстояния r от общей оси вращения на общую угловую скорость w. Для такого случая живая сила всей системы будет
W1 = 1/2∑mr2∙w2 = 1/2Jw2.
Здесь величина: J = ∑mr2, так наз. "М. инерции" относительно данной оси, заменяет коэффициент М, так наз. массу в выражении живой силы при прямолинейном движении с общей скоростью v, и служит мерой инерции при вращательном движении. Выражения такого же вида получаются и при рассмотрении иных вопросов: например в учении о сопротивлении строительных материалов излому (см.); поэтому-то определение М. инерции для тел разной формы неоднократно занимало математиков. Так как сумма масс всех частиц тела всегда равна его массе М, то М. инерции часто находят удобным выражать в виде произведения массы тела М на квадрат некоторой чисто геометрической величины К линейного измерения [измерение же М. ин. будет (l2, m, t0) в системе абсолютных мер]
∑mv2 = MK2, или: K2 = (∑mr2)/M.
Когда тело однородно и форма его определена геометрически, вычисление М. инерции становится задачей интегрального исчисления: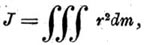
масса частицы становится dm, дифференциалом массы тела, а тройной интеграл распространяется на все это тело. Если сравнивать М. инерции одного и того же тела около осей, проходящих через разные его точки, но параллельных одному и тому же направлению, то наименьшим окажется М. инерции около оси, проходящей через центр тяжести. Действительно, для произвольно выбранной частицы тела, имеющей массу т, расстояния r' и r от выбранной оси и от оси, ей параллельной, проходящей через центр тяжести, образуют с расстоянием этих осей, d, косоугольный треугольник высотою h, представляющей расстояние рассматриваемой точки от общей плоскости осей, проходящей по условию через центр тяжести. По известной теореме: r'2 = r2 + d2 — 2hd, откуда: ∑mr'2 = ∑mr2mr2 + d2∑m — 2d∑hm. Но ∑m = M, массе тела, d величина постоянная, ∑mr'2 = J', ∑mr2 = J, a ∑hm = 0, так как именно этим условием и определяется положение центра тяжести тела. Поэтому, подставляя, получим:
J'= J + Md2.
Так как величина Md2 всегда положительная, то J' всегда больше J, момента инерции около оси, проходящей через центр тяжести. Пуансо предложил довольно сложное построение, дающее наглядное представление об изменениях М. инерции, когда ось меняет свое направление, продолжая проходить через одну и ту же точку тела. Пользуясь методом аналитической геометрии, будем определять наклон этой оси ее углами λ, μ, ν с прямоугольными осями координат, имеющими начало в рассматриваемой точке и составляющими одно целое с телом. Квадрат расстояния r от этой оси некоторой произвольно выбранной точки, определяемой координатами x, у, z, выразится разностью квадрата ее расстояния от начала координат и квадрата проекции этого расстояния на направление оси вращения, т. е.:
r2 = x2 + y2 + z2 — (xcosλ + ycosμ + zcosν)2
тогда момент инерции всего тела, J = ∑mr2, выразится уравнением такого вида: ∑mr2 = Acos2λ + Bcos2μ + Ccos2ν — 2αcosμcosν — 2βcosνcosλ — 2γсоsλсоsμ, где A = ∑m(y2 + z2), B = ∑m(z2 + x2), C = ∑m(x2 + y2), α = ∑myz, β = ∑mzx, γ = ∑mxy. Подставим теперь вместо ∑mr2 новую переменную, положив:
∑mv2 = 1/u3
и представим, что длина и отложена вдоль оси вращения от начала координат в положительную сторону; тогда ucosλ = ξ; ucosμ = η, ucosν = ζ будут выражать координаты некоторой точки, составляющей конец этой длины. После такой подстановки уравнение наше получит вид:
1 = Aξ2 + Bη2 + Cξ2 — 2αηζ — 2βζξ — 2γξη.
Если в нем ξ, η и ζ переменные, т. е. если предположить, что наклон оси вращения принимает последовательно все возможные величины, то оно будет изображать поверхность некоторого эллипсоида с вершиною в начале координат, а длина каждого полудиаметра этого эллипсоида, будучи обратно пропорциональна соответственному М. инерции тела, дает меру этой величины для оси того же наклона. В аналитической геометрии доказывается, что всякий эллипсоид имеет три взаимно перпендикулярные главные оси, одну наибольшую, другую наименьшую; третья в общем случае будет отличаться от первых двух, а для эллипсоида вращения будет равна одной из них. Главные оси эллипсоида инерции называются "главными осями инерции" тела. Если начало координат совпадает с центром тяжести, то эллипсоиду инерции придают название "центрального". Уравнение эллипсоида инерции принимает наипростейший вид, когда оси координат совпадают с главными осями инерции тела; тогда в полярных координатах, называя его главные полуоси а, b, с, будем иметь
1/u2 = (cos2λ)/a2 + (cos2μ)/b2 + (cos2ν)/c2
или
1 = x2/a2 + y2/b2 + z2/c2 в прямоугольных координатах. На основании этих двух теорем можно вычислить М. инерции тела около произвольно выбранной оси, если известны его М. инерции около главных осей центрального эллипсоида инерции. Вот эти величины, вычисленные для случаев часто встречающихся (причем во всех случаях М обозначает массу тела, K — его радиус вращения, J = MK2 — М. инерции, ρ — плотность, а ось проходит через центр тяжести). Для тяжелой прямой длиной l, образующей угол α с осью вращения, проходящей через ее середину:
J = 1/12(Ml2sin2α).
Эллипсоид инерции в этом случае будет эллипсоидом вращения с бесконечной длинной главной осью, направленной вдоль самой линии, т. е. для α = 0, J = 0. Для цилиндра дл. l и радиуса r: М= ρ2πlr2.
Около продольной оси: J = mr2.
Около поперечной оси: J = M[(1/12)l2 + (1/4)r2].
Для прямоугольного параллелeпипеда с ребрами a, b, с : М= ρabc.
Около оси α: J = (1/12)M(a2 + b2).
Для шара радиуса r: M = ρ(4/3)πr2, J = (2/5)Mr2.
Для эллипсоида с полуосями а, b, с: M = ρ(3/4)πabc.
Около оси a: J = (1/5)M(b2 + с2).
Для конуса высоты h и радиуса основания r:
M = (1/3)ρπr2h.
Для оси продольной J = (3/10)Mr2.
Для оси, параллельной основанию: J = M[r2 + (1/4)h2] (центр тяжести лежит на 1/4h, считая от основания).
Для цилиндрической трубки высоты l с внутренним радиусом r2, наружным r1 и полагая: 1/2(r1 + r2) = r, r1 — r2 = b
M = ρπl[(r1)2 — (r2)2] = ρ2πrbl.
Для продольной оси: J = (1/2)M[(r1)2 + (r2)2] = M[r2 + (1/4)b2].
Для поперечной оси:
J = (1/2)M[(1/12)l2 + (1/4)(r1)2 + (1/4)(r2)2] = M[(1/12)l2 + (1/2)r2 + (1/8)b2].
Для "тора" (круглого кольца, образующегося от вращения кружка радиуса r, которого центр описывает круг радиуса R около оси, заключающейся в его плоскости)
M = ρ2π2Rr2.
Для оси, нормальной к плоскости кольца:
J = M[(1/2)R2 + (3/4)r2].
Для оси поперечной: J = M[(1/2)R2 + (5/8)r2].
М. инерции тела, которого форма не может быть удобно определена геометрически, можно определить опытом. Для этого надо заставить его качаться наподобие маятника около горизонтальной оси, определить продолжительность его колебания Т и расстояние а между осью и центром тяжести (см.). Известно, что для простого маятника (см.) длиною l время колебания при ускорении силы тяжести g будет:
T = √(l/g), или T = π√(ml2/mgl),
если назовем m массу тяжелой частицы маятника. Но в числителе величина ml2 не что иное, как М. инерции этой частицы около оси вращения, а в знаменателе mgl означает произведение mq, веса частицы, на ее расстояние от оси вращения, так наз. "статический" момент. Когда же твердое тело совершает маятникообразные колебания продолжительности T, одни лишь частицы его, расположенные на прямой, проведенной на расстоянии l параллельно оси и в одной с нею вертикальной плоскости, во время покоя тела будут совершать это движение под влиянием одной своей тяжести mg. Каждая из остальных его частиц будет качаться так, как будто на нее действует сила q, равнодействующая из ее веса mg и внутренних замедляющих или ускоряющих сил, зависящих от связи этой частицы с остальными. Но все частицы тела совершают свои колебания одновременно, значит:
l/g = ml2/mgl = ml'2/ql' = ml"2/ql" =... = (∑ml2)/(∑ql).
Здесь ∑ml2 и есть искомый М. инерции, равный МК2, а стоящая в знаменателе сумма ∑ql = Mga, весу тела, помноженному на расстояние a его центра тяжести от оси вращения, потому что сумма всех моментов внутренних сил равна нулю, так как они не могут привести тело в движение вследствие равенства действия и противодействия. Итак:
T = π√(MK2/Mga) = π√(K2/ga) = π√(l/g)
откуда l = K2/a, K2 = la,
т. е. искомый квадрат радиуса вращения равен произведению длины простого маятника, совершающего колебание в то же время, что и наблюдаемое тело, на расстояние его центра тяжести от оси вращения. При магнитных измерениях М. инерции часто определяют по качаниям, совершаемым под влиянием сил магнитного поля.
В. Л.
| "БРОКГАУЗ И ЕФРОН" >> "М" >> "МО" >> "МОМ" |
Статья про "Момент инерции" в словаре Брокгауза и Ефрона была прочитана 3448 раз
| Пицца в сковороде |
| Семга на горелке |
TOP 15
- Волос
- Проно
- Степные животные
- Гимнастика
- Индийский океан
- Архитектура
- Сравнение, в литературе
- Манда
- Клитры
- Колесование
- Испарение
- Травоядные животные
- Оплодотворение у pacтений
- Вредные насекомые
- Электризация тел