


БНБ
"БРОКГАУЗ И ЕФРОН" (121188)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Логарифм
Определение "Логарифм" в словаре Брокгауза и Ефрона
Логарифм — Л. данного числа n называется показатель степени, в которую нужно возвести некоторое другое данное число а, называемое основанием, чтобы получить n; так что зависимость между данным числом n, основанием а и Л. х числа n выражается формулою n = a х. Л. числа обозначается символом log, или lg, или L. Л. числа n, взятый при основании а, обозначается иногда так: lgan, причем всегда должно удовлетворяться равенство n = algan. Например, из равенства 1000=10 3 следует 3=lg 10 1000. Из равенства n= а lgan вытекают свойства логарифмов, обусловливающие полезность этой функции, а именно: 1) Л. произведения равен сумме Л. производителей; 2) Л. частного равен разности Л. делимого и делителя; 3) Л. степени равен произведению показателя степени на число, возводимое в степень; 4) Л. корня равен Л. подкоренной величины, разделенному на показатель корня. Эти свойства выражаются формулами:
lg(uv) = lgu + lgv;
lg(u/v) = lgu — lgv;
lg(um) = mlgu;
lgm√u = lgu/m.
Обладая такими свойствами, Л. дают возможность свести: умножение на сложение, деление на вычитание, возведение в степень на умножение и извлечение корня на деление, что и выясняет огромное практическое значение Л. для всех, кто имеет дело со сложными арифметическими вычислениями. При нашей десятичной системе исчисления самым удобным основанием оказывается число 10; имеется и множество таблиц, в которых даются Л. последовательных чисел начиная от 1 до 100000. При основании, равном 10, только Л. целых степеней десяти суть целые числа, Л. же простых чисел представляются десятичными дробями, например lg 30=1,4771213. Целая часть такой дроби наз. характеристикою, а дробная — мантиссою. Характеристика определяется прямо по числу цифр целой части числа, именно, она равна числу таких цифр без единицы. Например, для числа 354,25, имеющего три цифры в целой части, характеристика будет 2. Благодаря такому легкому способу определения характеристики в таблицах дается лишь одна мантисса. Для большего упрощения вычислений самое вычитание Л. заменяется обыкновенно сложением, для чего вводят вместо вычитаемого Л. дополнение этого Л. Дополнением называется разность между Л. и числом 10. Если характеристика данного Л. более 10, то характеристика дополнения будет отрицательная, что и обозначается знаком -, который ставится над нею; например, дополнение от 12,3542351 будет 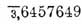 . Вычесть из одного Л. другой Л. все равно, что придать к первому Л. дополнение второго и из результата вычесть 10. Для уяснения пользы, приносимой Л. при вычислениях, возьмем два примера. 1) Определим конечный результат арифметических действий, выражаемых формулой x =(53126·32135)/(25677·62353). Производя эти действия обыкновенными приемами, мы должны были бы исписать довольно много бумаги; с помощью Л. задача решается тем, что подыскиваются в таблице Л. чисел, стоящих в числителе, и Л. чисел, стоящих в знаменателе, из последних в уме определяются их дополнения, и все это складывается следующим образом:
. Вычесть из одного Л. другой Л. все равно, что придать к первому Л. дополнение второго и из результата вычесть 10. Для уяснения пользы, приносимой Л. при вычислениях, возьмем два примера. 1) Определим конечный результат арифметических действий, выражаемых формулой x =(53126·32135)/(25677·62353). Производя эти действия обыкновенными приемами, мы должны были бы исписать довольно много бумаги; с помощью Л. задача решается тем, что подыскиваются в таблице Л. чисел, стоящих в числителе, и Л. чисел, стоящих в знаменателе, из последних в уме определяются их дополнения, и все это складывается следующим образом: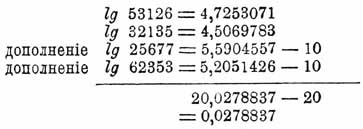
Ближайший к нему Л. в таблицах имеет мантиссу 0278794, и ему соотвтствует в таблице число 10663; соответствующее число должно иметь одну цифру в целой части; если возьмет 1,0668, то это число выразит собою искомое число с точностью 0,0001. 2) Найдем 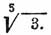 . Обыкновенная алгебра даже не дает никаких других приемов для вычисления такого радикала кроме логарифмирования, посредством которого задача решается тем, что отыскивается в таблице lg3=0,4 771213; делением этого Л. на 5 получается 0,0954242, ближайший к этому логарифм в таблицах находим: 0,0954135 , которому соответствует в таблице число 1,2457; это и будет
. Обыкновенная алгебра даже не дает никаких других приемов для вычисления такого радикала кроме логарифмирования, посредством которого задача решается тем, что отыскивается в таблице lg3=0,4 771213; делением этого Л. на 5 получается 0,0954242, ближайший к этому логарифм в таблицах находим: 0,0954135 , которому соответствует в таблице число 1,2457; это и будет 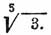 с точностью 0,0001. Логарифмы были изобретены шотландским геометром Непером (Napier), который в 1614 году напечатал "Mirifici logarithmorum canonis descriptio", посвященное им принцу Валлийскому (впоследствии король Карл I). Это сочинение in 4° представляет 56 страниц текста и 90 страниц таблиц; оканчивается оно словами: "собирая плоды этого небольшого произведения, воздайте должную славу и благодарность Богу высшему создателю и расточителю всех благ". Непер принял за основание своих таблиц особое несоизмеримое число, имеющее чрезвычайно важное значение в анализе и обозначаемое обыкновенно через е. Такой выбор основания поясняется следующими соображениями. Пусть α есть весьма малая величина, а — основание какой-либо системы; тогда члены арифметической прогрессии: 0, α, 2 α, 3 α... представят собою Л. членов геометрической прогрессии: 1, а α, а 2 α , а 3 α ..., в которой знаменатель отношения а α, благодаря малости а, весьма мало отличается от 1. Назовем через β ту малую величину, на которую а α отличается от 1, так что a α =1+ β; положим α / β=M. Тогда арифметическая прогрессия примет вид: 0, Mβ, 2M β, 3M β..., геометрическая же обратится в (1+β)0, (1+ β)1, (1+ β)2... Количество β совершенно произвольно: известно только, что оно очень мало; множитель же M зависит от того, какое мы избрали основание. Самое простое положить M =1. Основание, при котором М=1, и выбрано было Непером для его таблиц. Определим его величину: при М=1 упомянутая арифметическая прогрессия обращается в: 0, β, 2 β, 3 β..., геометрическая есть (1+β)0, (1+ β)1, (1+ β)2...; основание есть то число, которого Л. равен единице; положим, что (m+1) ый член арифметической прогрессии равен 1, то есть что m β=1, тогда соответствующий член (1+β)m геометрической прогрессии и будет основанием, при котором М=1. Подставим в этот член вместо β его величину из m β=1, получим [1+(1/ m)]m. Эта величина и будет основанием неперовых Л., так что, разлагая до бинома Ньютона, получим
с точностью 0,0001. Логарифмы были изобретены шотландским геометром Непером (Napier), который в 1614 году напечатал "Mirifici logarithmorum canonis descriptio", посвященное им принцу Валлийскому (впоследствии король Карл I). Это сочинение in 4° представляет 56 страниц текста и 90 страниц таблиц; оканчивается оно словами: "собирая плоды этого небольшого произведения, воздайте должную славу и благодарность Богу высшему создателю и расточителю всех благ". Непер принял за основание своих таблиц особое несоизмеримое число, имеющее чрезвычайно важное значение в анализе и обозначаемое обыкновенно через е. Такой выбор основания поясняется следующими соображениями. Пусть α есть весьма малая величина, а — основание какой-либо системы; тогда члены арифметической прогрессии: 0, α, 2 α, 3 α... представят собою Л. членов геометрической прогрессии: 1, а α, а 2 α , а 3 α ..., в которой знаменатель отношения а α, благодаря малости а, весьма мало отличается от 1. Назовем через β ту малую величину, на которую а α отличается от 1, так что a α =1+ β; положим α / β=M. Тогда арифметическая прогрессия примет вид: 0, Mβ, 2M β, 3M β..., геометрическая же обратится в (1+β)0, (1+ β)1, (1+ β)2... Количество β совершенно произвольно: известно только, что оно очень мало; множитель же M зависит от того, какое мы избрали основание. Самое простое положить M =1. Основание, при котором М=1, и выбрано было Непером для его таблиц. Определим его величину: при М=1 упомянутая арифметическая прогрессия обращается в: 0, β, 2 β, 3 β..., геометрическая есть (1+β)0, (1+ β)1, (1+ β)2...; основание есть то число, которого Л. равен единице; положим, что (m+1) ый член арифметической прогрессии равен 1, то есть что m β=1, тогда соответствующий член (1+β)m геометрической прогрессии и будет основанием, при котором М=1. Подставим в этот член вместо β его величину из m β=1, получим [1+(1/ m)]m. Эта величина и будет основанием неперовых Л., так что, разлагая до бинома Ньютона, получим
e = (1+m/1)m = 1 + m(1/m) + [m(m-1)/1.2]1/m2 +... или
e = (1+1/m)m = 1 + 1 + (1-1/m)/1.2 + [(1-m/1)(1-2/m)]/1.2.3 +...;
так как β весьма мало, то m весьма велико, и дроби, содержащие m в знаменателе, по малой их величине можно отбросить; таким образом получим:
e = 1+1+(1/1.2)+(1/1.2.3)+(1/1.2.3.4)+...=2,71828.
Неперовы Л. называются иногда гиперболическими или натуральными; натуральными потому, что проще всего было предположить М=1; гиперболическими потому, что если в равносторонней гиперболе, отнесенной к асимптотам, принять абсциссу вершины за единицу, то площадь, заключенная между гиперболою, осью абсцисс, ординатою вершины и ординатою, соответствующею абсциссе x, равна lgx в неперовой системе. Величина е имеет особенно важное значение в анализе благодаря существованию ряда:
ex = 1+x+(x2/1.2)+(x3/1.2.3)+(x4/1.2.3.4)+...;
благодаря способности разлагаться в такой ряд показательная функция e х служит переходом от алгебраических функций к тригонометрическим, потому что из сравнения этого ряда с разложениями cosx и sinx следуют формулы: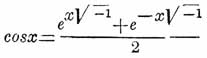 ;
; 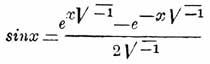 .
.
Зная Л. числа m при данном основании а, можно определить Л. х числа m и при всяком другом основании b, потому что из равенства m=е следует lgm=xlgab, откуда: х=lg bm=(lgam)/(lga b); из этой формулы видно, что, имея Л. числа m при основании а, следует только помножить его на 1/(lg a b), чтобы получить Л. числа m при основании b. Множитель, служащий для перехода от одной системы к другой, называется модулем. Модуль, на который следует множить неперовы Л. для получения Л. при основании 10, равен 0,4349448. Л. удовлетворяют, между прочим, следующим замечательным рядам: lg(1+x)=(x — x2/2 + x3/3 + x4/4 +...)M, где M есть модуль для перехода от неперовых Л.; lg(n+1)-lgn = 2M[1/(2n+1) + 1/3(2n+1)3 + 1/5(2n+1)5 +...]. Посредством последнего, весьма быстро сходящегося ряда обыкновенно и вычисляются Л. следующим образом: зная, что lg100=2, подставим в наш ряд 100 вместо n; получим lg101 — 2 = M(1/201 + 1/3.2013 + 1/5.2015 +...); последующие члены ряда, стоящего в скобках, уже настолько малы, что ими можно пренебречь и простым вычислением получить lg101=2,0043214; зная lg101, получим lg102 и так далее. Понятие о Л. обобщается распространением логарифмирования и на мнимые функции; при этом получаются формулы: lg(a+bi) = lg[r(cos φ +isin φ)] = lgr + (2n π + φ)i, где i=√(-1), r=√(a2+b2), cos φ =a/[√(a2+b2)], sin φ =b/[√(a2+b2)]
Кроме Л. чисел, в таблицах обыкновенно помещаются Л. тригонометрических величин (см. Тригонометрические таблицы). Первые таблицы, в которых за основание было принято число 10, были напечатаны другом Непера Бриггом в 1624 г. под заглавием "Arithmetica logarithmica". В таблице Бригга были даны Л. чисел, начиная с 1 до 20000 и от 90000 до 1 00000, с 14 знаками в мантиссе. Голландский математик Влакк (Adrien Vlacq) пополнил пробел бригговских таблиц и напечатал в 1628 г. таблицы, содержащие Л. всех чисел от 1 до 100000, с десятью знаками в мантиссе. Из последующих изданий наиболее известны таблицы Гардинера, Баббаджа и Тейлора. В настоящее время употребляются чаще всего при вычислениях таблицы Каллета (до 106000), карманные таблицы Лаланда с пятью знаками и таблицы Бремикера семизначные, представляющие обработку таблиц Веги "Thesaurus logarith m orum completus" (1794). Существуют и весьма распространены у нас русские табл. Бремикера, напечатанные стереотипно.
Гауссовы Л. Для определения Л. суммы и разности двух чисел по Л. этих чисел Гаусс изобрел особые таблицы. Лучшие издания Гауссовых Л. представляют издания Витштейна, Матиссена и Цеха.
Н. Делоне.
| "БРОКГАУЗ И ЕФРОН" >> "Л" >> "ЛО" >> "ЛОГ" |
Статья про "Логарифм" в словаре Брокгауза и Ефрона была прочитана 1613 раз
| Бургер двойного помола |
| Английская картошка фри |
TOP 15
- Волос
- Проно
- Степные животные
- Гимнастика
- Индийский океан
- Архитектура
- Сравнение, в литературе
- Манда
- Клитры
- Колесование
- Испарение
- Травоядные животные
- Оплодотворение у pacтений
- Вредные насекомые
- Электризация тел