


БНБ
"БРОКГАУЗ И ЕФРОН" (121188)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Линейное преобразование
Определение "Линейное преобразование" в словаре Брокгауза и Ефрона
Линейное преобразование — Л., или проективным, преобразованием плоскости называется такой переход от одной плоскости к другой, при котором все точки любой прямой, лежащей в первой плоскости, образуют во второй плоскости тоже прямую. Этот переход достигается преобразованием координат х', у' в координаты x, у по формулам: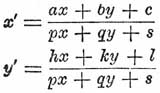
Л. преобразованием форм, т. е. многочленов однородных относительно переменных, называется такое преобразование, в котором новая форма получается из данной заменой переменных многочленами однородными первой степени от новых переменных. Напр.: линейное преобразование двоичной формы (содержащей две переменных x и у) совершается посредством формул: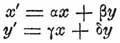
где α, ß, у, δ называются коэффициентами преобразования. Определитель 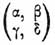 называется модулем такого преобразования (см. Форма).
называется модулем такого преобразования (см. Форма).
| "БРОКГАУЗ И ЕФРОН" >> "Л" >> "ЛИ" >> "ЛИН" >> "ЛИНЕ" |
Статья про "Линейное преобразование" в словаре Брокгауза и Ефрона была прочитана 710 раз
| Английский рыбный пирог |
| Английский рыбный пирог |
TOP 15
- Волос
- Проно
- Степные животные
- Гимнастика
- Индийский океан
- Архитектура
- Сравнение, в литературе
- Манда
- Клитры
- Колесование
- Испарение
- Травоядные животные
- Оплодотворение у pacтений
- Вредные насекомые
- Электризация тел