


БНБ
"БРОКГАУЗ И ЕФРОН" (121188)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Качка корабля
Определение "Качка корабля" в словаре Брокгауза и Ефрона
Качка корабля — К. назыв. боковою, если корабль качается около своей продольной оси (с боку на бок), и килевою, если корабль качается около поперечной оси, т. е. погружаясь попеременно то носом, то кормой. Плавная, спокойная, небольших размахов К. на волнении есть одно из важнейших мореходных качеств корабля, поэтому выяснением тех условий, от которых оно зависит, занимались почти все ученые, писавшие о теории корабля, начиная с Иоанна и Даниила Бернулли и Эйлера, но лишь в 1861 г. В. Фруд дал теорию боковой К. на волнении, хотя и приближенную, но достаточно удовлетворительную. Оказывается, что о К. корабля на волнении можно судить по качаниям корабля на тихой воде. Если корабль на тихой воде вывести каким-нибудь образом из прямого положения, наклонив его на бок на небольшой угол и предоставить самому себе, то вследствие остойчивости он будет стремиться вернуться в прямое положение и поэтому начнет вращаться около продольной оси, проходящей через его центр тяжести; придя в прямое положение, корабль не остановится в нем, а по инерции будет продолжать вращение и уклонится на другую сторону на некоторый угол, который вследствие сопротивления воды будет несколько меньше первого. Таким образом, корабль будет совершать ряд размахов убывающей величины подобно маятнику, качающемуся в сопротивляющейся среде. Пока величина размаха на сторону (амплитуда) не превышает 10° — 15°, то продолжительность их почти не зависит от величины размаха. Эта продолжительность одного размаха называется периодом естественных качаний корабля и зависит от его момента инерции относительно продольной оси, проходящей через центр тяжести корабля, и расстояния от центра тяжести до метацентра (см. Остойчивость) и выражается такою формулой: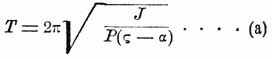
где J — сказанный момент инерции корабля, P его вес (ς — α) расстояние от центра тяжести корабля до метацентра, Т — период двойного размаха, самое же движение корабля выразится формулой φ = C1sin(2 π t/T) + C2cos(2 π t/T), где φ — угол наклонения корабля в момент t, C1 и С 2 — некоторые постоянные, значения которых определяются по начальным условиям, напр. если при t = 0 корабль был наклонен на угол φ = φ 0 и затем был предоставлен самому себе без начальной скорости, то С 1 = 0, С 2 = φ 0 и движение корабля выразится формулой φ = φ 0cos(2 π t/T). Эта формула, совершенно подобная формуле физического маятника, выведена в предположении, что вода не представляет сопротивления движению. Но сопротивление среды изменяет величину размахов, лишь в слабой степени влияя на их продолжительность, так что (а) формула остается справедливой и при сопротивлении. Закон уменьшения амплитуды размахов зависит от того, как выражается сопротивление среды в функции скорости. Так, если сопротивление пропорциально первой степени скорости, то амплитуды размахов убывают в геометрической прогрессии, когда число их возрастает в арифметической, если же сопротивление пропорционально второй степени скорости, то амплитуды убывают по такому закону:
θ (n+1) — θ n = — a θ n2 (1)
где θ n амплитуда n-го размаха, θ (n+1) — амплитуда (n+1)-го, a некоторая постоянная. Наконец, если сопротивление среды выражается двумя членами, из которых один пропорционален первой, другой второй степени скорости, то закон убывания амплитуд выражается формулой:
θ (n+1) — θ n = — (a θ n + b θ n2) (2)
где а и b некоторые постоянные. По испытаниям, произведенным Фрудом и Бертэном, оказывается, что обе формулы достаточно точно согласуются с опытом. Вопрос о качке корабля на волнении решен Фрудом при таких предположениях: 1) что размахи корабля изохронны, т.е. продолжительность их не зависит от амплитуды, 2) продольная ось корабля параллельна гребню волны, 3) что поперечные размеры корабля весьма малы относительно размеров волны, 4) что волны трохоидальные (см. Волны) и волнение установившееся. При таких предположениях, не принимая во внимание сопротивления воды, Фруд показал, что закон качаний корабля может быть выражен формулой:
ψ = (φ + θ) = C1sin(2 π t/T) + C2cos(2 π t/T)+ [(τ 2 Θ)/(τ 2 — T2)] sin(2 π t/ τ). .(2)
где ψ угол наклонения корабля от отвесной линии, φ угол наклонения корабля относительно поверхности волны, θ наклонение поверхности волны в точке занимаемой в момент t кораблем к горизонту, Т период естественных качаний корабля, τ период волны, Θ наибольшее наклонение поверхности волны к горизонту. Заметим, что, когда высота волны незначительна относительно ей длины, то
θ = Θ sin(2 π t/ τ).
C1 и С 2 — некоторые постоянные, зависящие от начальных условий, т. е. от начального наклонения корабля и его начальной угловой скорости.
Из этой формулы можно вывести следующие главнейшие заключения:
1) Если отношение τ /T, т. е. (период волны)/(период корабля) весьма мало, то последний член формулы можно отбросить по его малости и, значит, корабль будет качаться совершенно так же, как на тихой воде, при тех же начальных условиях; иными словами — волны, период которых мал относительно периода корабля, не влияют на него.
2) Если отношение τ /T весьма велико, но последний член формулы можно написать так: Θ sin(2 π t/ τ), и тогда φ = C1sin(2 π t/T) + C2cos(2t/T), т. е. корабль будет качаться относительно волновой поверхности точно так же, как он при тех же начальных условиях качался на тихой воде относительно ее поверхности, при этом, если принять в расчет сопротивление воды, то эти размахи, зависящие от начальных условий, быстро пропадут и останется φ = 0 и ψ = θ, т. е. корабль будет следовать за волной, оставаясь своими мачтами нормальным к ее поверхности.
Если τ = T, т. е. период волны равен периоду корабля, то формула (2) не имеет места и вместо нее будет такая:
φ = C1sin(2 π t/T) + C2 sin(2 π t/T) — (π / τ) Θ tcos(2 π t/ τ)
которая показывает, что размахи неопределенно возрастают вместе с временем t, т. е. не могут оставаться малыми, как предполагалось при выводе формулы.
Фруд на опыте над моделями кораблей показал, что когда модели подвергались действию волн периода, равного их периоду качаний, то после нескольких волн они опрокидывались. Этого не будет с настоящими кораблями благодаря сопротивлению воды его качаниям, но все-таки его К. будет весьма сильная.
Чтобы оценить влияние сопротивления воды на качания корабля, можно из опытов над уменьшением размахов К. на тихой воде определить величину сопротивления воды качаниям корабля; приняв, напр., это сопротивление пропорциональным второй степени скорости и допуская, что этот коэффициент пропорциональности сохраняет свою величину и при К. на волнении, можно составить уравнения его движения на волне; интегрирование их и дает требуемый закон качаний корабля на данной волне. Но Фруд показал, что можно с достаточным приближением принять, что уменьшение амплитуды размахов при К. на волнении будет выражаться тою же формулой и с теми же коэффициентами, как и на тихой воде. Тогда не трудно рассчитать предельную величину размаха корабля для того случая, когда он встретит волны, период которых равен его собственному; это будет: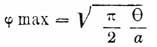 ,
,
если предположить, что убывание амплитуд выражается формулою (1).
Для увеличения сопротивления воды качаниям корабля устраивают боковые кили. Кроме того, на некоторых английских судах ("Inflexible", "Edinburgh") устраивали особые отделения, заполнявшиеся водою наполовину, — вода, переливаясь в них с борта на борт, погашает размахи качки. После начала постройки броненосного флота во Франции были образованы особые комиссии для выяснения мореходных качеств этого нового типа кораблей. Особенно замечательны результаты наблюдений, полученных в 1863 г. при испытании броненосных фрегатов, сравнительно с деревянными винтовыми кораблями. На них постоянно тщательно наблюдалась величина размахов боковой К., и результаты этих наблюдений были сведены в такую таблицу:
| Hазвание корабля | Относительная величина размахов качки по сравнению с размахами кор. Napol éon | Полупериод T/2 боковой качки (секунды) |
| Tourville, деревян. корабль | 0,815 | 5,51 |
| Solferino, броненосн. корабль | 0,820 | 5,91 |
| Magenta, броненосн. корабль | ||
| Napolé on, винтов. корабль | 1,000 | 5,82 |
| Couronne, брон. фрегат | 1,168 | 4,94 |
| Invincible, броненосн. фрегат | 1,780 | 4,83 |
| Normandie, броненосн. фрегат |
Во время плавания 1870-1872 г. броненосный корабль Oc é an обращал на себя внимание почти полным отсутствием качки, размахи которой не превышали 3° — 4° на сторону; в это же время броненосные крейсера Armide, Thetis, Reine-Blanche качались с размахами от 30° до 40°. Oc é an обладал весьма малою метацентрическою высотою (ρ — α) = 0, м 60, и полупериод его был 9,93 секунды, полупериод же сказанных фрегатов был 5,с 70; 5, с 18 и 6,с 02. В 1879 году был снова произведен целый ряд систематических наблюдений над качкою кораблей, результаты чего и данные о кораблях сгруппированы в следующей таблице,
| Hазвание корабля | Водоизмещен., тонны | Длина корабля, метры | Метацентрич. высота (ρ — α), метры | Полупериод размахов T /2, секунды | Средняя амплитуда размахов |
| Richelieu, броненосный корабль 1-го ранга | 8790 | 98,70 | 0,63 | 8,95 | 1° — 2° |
| Trident, броненосный корабль 1-го ранга | 8814 | 98,00 | 0,67 | 9,00 | 2° — 3° |
| Suffren, броненосный корабль 1-го ранга | 7604 88,70 | 0,71 | 8,75 | 1° — 2° | |
| Colbert, броненосный корабль 1-го ранга | 8617 | 98,00 | 0,80 | 7,63 | 2°-3° |
| Friedland, броненосный корабль 1-го ранга | 8824 | 95,70 | 0,80 | 8,00 | 3° — 4° |
| Redoutable, броненосный корабль 1-го ранга | 8858 | 96,70 | 0,94 | 7,34 | 3° — 4° |
| Revanche, брон. фрегат | 5900 | 81,60 | 1,35 | 6,00 | 16° — l7° |
| Duquesne, крейсер 1 ранга | 5824 | 99,64 | 1,67 | 5,18 | 21° |
| Tourville, крейсер 1 ранга | 5740 | 99,00 | 1,66 | 5,04 | 16° — 17° |
| Hirondelle, посыльное судно | 1162 | 76,65 | 1,09 | 5,83 | 25° — 27° |
| Desaix, посыльное судно | 1684 | 77,00 | 1,40 | 4,51 | 25° — 27° |
Из последних двух столбцов этой таблицы особенно ясно видно, какое значение имеет период качки корабля на величину ее размахов. Подробное изложение теории качки корабля см. в сочинении Pollard et Dudebout, "Theorie du Navire" (Париж, 1891-1894). Вышеприведенные таблицы заимствованы из этого сочинения.
А. Крылов.
| "БРОКГАУЗ И ЕФРОН" >> "К" >> "КА" >> "КАЧ" |
Статья про "Качка корабля" в словаре Брокгауза и Ефрона была прочитана 1447 раз
| Пицца в сковороде |
| Яйца в кляре |
TOP 15
- Волос
- Проно
- Степные животные
- Гимнастика
- Индийский океан
- Архитектура
- Сравнение, в литературе
- Манда
- Клитры
- Колесование
- Испарение
- Травоядные животные
- Оплодотворение у pacтений
- Вредные насекомые
- Электризация тел