


БНБ
"БРОКГАУЗ И ЕФРОН" (121188)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Интерференция
Определение "Интерференция" в словаре Брокгауза и Ефрона
Интерференция (физ.) — содействие или противодействие двух или большего числа волн, происходящих от колебательных, периодически повторяющихся движений. Волны (см.) могут происходить в жидкостях, твердых телах, газах и эфире. В первом случае И. волн видима непосредственно, во втором и третьем — результаты И. слышимы, но наблюдаются и оптически; это звуковая И. Волны эфира могут произвести И. света и теплоты, подобные же волны вероятно производят и те электрические явления, для объяснения которых нужно допустить И. Движение водяных волн есть только кажущееся, т. е. движущаяся волна не несет одни и те же частицы воды, а беспрестанно составляется из новых частиц, находящихся на направлении ее кажущегося движения. Подобно этому и волны звуковые и эфирные представляют в сущности движение, передающееся по известному направлению от одних частиц к следующим, причем каждая частица движется взад и вперед лишь между определенными пределами по законам гармонического движения (см.). Воздушные частицы совершают колебательные движения по направлению его распространения, а эфирные — в плоскости, перпендикулярной к направлению распространения. Если по одному направлению или по двум, весьма близким одно к другому, направлениям передаются два движения, то частицы на всем пути его будут двигаться по таким направлениям и принимать такие положения, которые будут результатом совокупного действия двух систем движения. В статье волны объяснено, что звуковые воздушные волны состоят из ряда последовательно перемежающихся слоев или столбов воздуха, то сгущенного, то разреженного. Если бы возникли две системы волн по одному направлению и случилось бы так, что в некоторой части одной системы в определенный момент образовался бы слой разреженного воздуха и в тот же момент в том же самом месте образовался бы слой сгущенного воздуха от другой системы, при отдельном существовании каждой, то при совместном существовании этих систем не может быть в рассматриваемом месте ни полного разрежения, ни полного сгущения воздуха. В этом месте будет или слабейшее разрежение, или слабейшее сгущение, или даже воздух придет вполне в состояние нормальной плотности и покоя. Подобное изменение одной системы волн другой и есть И.; говорят: волны интерферируют между собой. Вместо рассматривания сгущений и разрежений в предыдущем случае можно рассматривать направление и величину движения некоторой воздушной частицы (или целого ряда их), происходящего от сложения двух движений, сообщаемых в некоторый общий момент этой частице двумя системами колебаний. Из чертежа 2 видно, что в системе звуковых волн — одни воздушные частицы движутся вперед по направлению движения, в то время как другие движутся назад, и что вообще в одном и том же месте движение вперед сменяется движением назад, и обратно. От действия двух систем каждая воздушная частица будет находиться в одном из двух случаев: на нее будут действовать силы, или направленные в одну общую сторону, или же — в стороны противоположные. В первом случае частица будет двигаться с большей скоростью, чем она двигалась бы от одной силы, но в прежнюю сторону; в другом случае она может продолжать свое движение тоже в прежнюю сторону, но медленнее прежнего, или же частица пойдет в сторону, противоположную прежней, или, наконец, она останется неподвижной под влиянием двух равных и противоположных сил. Происходящие от И. двух волн явления весьма удобно могут быть истолкованы графическими приемами. Фиг. 1 ABCDE изображает символически форму волны (см. Волны), которая есть синусоида; каждая часть, обращенная кверху (выпуклая), с каждой частью, обращенной книзу (вогнутой), составляют волну, длина которой равна двойной длине (АЕ) каждой из частей.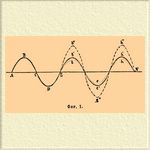
Фиг. 1
Расстояние каждой точки кривой линии от прямой (оси абсцисс), служащей основанием чертежа, показывает удаление этой точки от той, в которой она находилась в положении равновесия, т. е. до начала движения; все частицы воздуха, приходящиеся против выпуклой части кривой, движутся вперед по направлению распространения волн, а все точки против вогнутой ее части движутся назад. Фиг. 1 изображает символически две системы волн одинаковой длины, из которых одна система (изображенная сплошной линией) начинается в точке А; другая, изображенная пунктирной линией, — в точке Е. Расстояние между А и E называется разностью хода и в случае, изображенном на чертеже, составляет целую волну [Разность хода определяется прямой линией, измеряемой длиной волны или ее частями. Можно рассматривать изменение расстояния воздушных точек от положения равновесия по формуле у = a Sin2 π T/t, в которой у есть искомое расстояние, а — величина полуразмаха или наибольшее расстояние частицы от положения равновесия, Т - продолжительность одного полного колебания, принимаемая за единицу времени, t - время, измеряемое этой единицей, протекшее от начала колебания частицы до рассматриваемого момента; π есть численное отношение окружности к диаметру. Величина у, изменяющаяся от +а до -а, зависит от периодически изменяющейся величины 2π T/t или oт T/t, т. е. от изменений фазы движения. Этот термин употреблен в ст. Дифракция; вместо разности хода можно рассматривать разность фаз — заключения остаются одинаковыми. Уравнение более полное, чем вышеприведенное, см. ст. Волны; о фазах см. Колебательные движения.]. Начиная от точки С обе системы интерферируют между собой, вследствие чего образуется новая система Eb"e"h"N, в которой волны будут иметь прежнюю длину, но высота линий и понижение их увеличатся, так как происходят от сложения прежних высот и понижений. Но увеличение высот и углублений при той же длине волн, а следовательно, при прежней продолжительности колебаний, соответствующее увеличению размаха частиц, указывает на увеличение скорости движения частиц и на усиление степени сгущения и разрежения воздуха, а вместе с тем на усиление звука. В случае, изображенном на чертеже, две системы волн содействуют одна другой; содействие волн и соответственное усиление звука будут происходить вообще при разности хода, равной всякому целому числу волн или четному числу полуволн. Если бы обе системы начинались в точке А или точке С, и не было бы никакой разности хода (т. е. она была бы равна нулю), то и в этом случае произошло бы то же самое. Другой случай И. изображен на фиг. 2, где разность хода двух систем волн ABCDEF и AB'C'D'E'F составляет половину волны; когда все точки части одной системы подняты вверх, то соответственные другой — опущены вниз; при совместности обоих требований все точки между А и F должны остаться на прямой линии, т. е. оставаться неподвижными: волны уничтожатся, поэтому и звука не будет.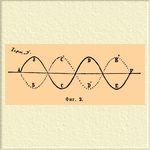
Фиг. 2
Если бы высоты волн (т. е. размахи частиц) обеих систем были неодинаковы, то осталась бы часть преобладающей волны и звук только ослабел бы, а не уничтожился, как в первом случае. Итак, при этой разности хода волны противодействуют одна другой, как и вообще при разности хода, составляющей 1, 3, 5 — и вообще нечетное число полуволн. Две системы звуковых волн, представляющие разность хода большую, чем полуволна, и меньшую целой волны, интерферируя между собой, образуют новую систему, в которой волны будут прежней длины, но при решении этого случая графически окажется, что новая система волн будет сдвинута относительно прежних; сила звука будет слабее, чем при полном совпадении волн, но во всех случаях высота тона остается одна и та же. Наблюдать эти случаи И. можно посредством прибора, состоящего из двух металлических трубок сифонной формы, вдвигаемых одна в другую. Кроме того, к одной из них приделаны поперек две коротенькие трубочки D и В, обращенные свободными концами наружу; в одну (D) принимается звуковая волна от маленькой органной трубки; волна, разделенная в приборе на две, по другую сторону его опять соединяется в одно целое во второй короткой трубке (В). Выдвигая одну трубку из другой, можно этим удлинить путь одной волны и таким образом делать разность хода обеих волн последовательно равной одной, двум, трем половинам длины волны, но акустически трудно в этом приборе наблюдать явления И. В приборе Кенига при второй трубке помещается маленькая газовая горелка, которой пламя остается в покое в случае уничтожения звука (потому что разрежение одной волны совпадает со сгущением другой и потому воздух остается в покое) и приходит в более или менее быстрое движение при разностях хода, соответствующих усилению звука. И. звуковых волн происходит в органных трубах, как закрытых, так и открытых. Здесь интерферирует волна, распространяющаяся в трубе, начиная с того конца, в который вдувают воздух, с той же волной, отразившейся от противоположного конца трубы (даже если он открыт). Здесь образуются так называемые стоячие волны (см.). В открытой органной трубе поперечный слой воздуха, приходящийся приблизительно в середине трубы, остается неподвижным, и в нем только происходят попеременно то сгущения, то разрежения воздуха, тогда как по обе стороны этого слоя, называемого узловым, воздух находится в движении — одновременно — то к узловой плоскости, то одновременно же от нее. В закрытой органной трубе узловая плоскость находится на дне трубки. Подробнее см. Органные трубы. О дифракции звука, которая, как явление, могла быть ожидаема для воздушных волн — см. Дифракция звуковая. Вышеизложенные результаты И. происходят в том случае, когда интерферирующие между собой волны имеют одинаковую длину, т. е. производят ощущение музыкальных тонов одной и той же высоты. Если же волны одной системы несколько длиннее или короче волн другой системы, то, почти совпадая в некоторый момент, они через несколько времени (или на некотором расстоянии от точки совпадения) начинают расходиться одна от другой, так что при графическом способе их изображения выпуклости их расходятся между собой, так же как и вогнутости. По истечении еще большего времени выпуклость одной волны приходится над вогнутостью другой, и если волны обеих систем одинаковой высоты, то одна волна почти (почти — потому что они неодинаковой длины) уничтожается другой; в этом случае разреженная часть воздушной волны совпадает со сгущенной частью другой и звук совершенно затихает, тогда как в начале, при взаимном содействии тел, звук имел наибольшую силу. Но после момента взаимного уничтожения волн они опять вследствие разности их длины расходятся, звук постепенно усиливается и, дойдя до наибольшей величины, опять ослабевает. Эти периодические повторения усиления и ослабевания звука, называемые дрожаниями тона (см. Диссонанс), могут быть хорошо замечены, если ударом молоточка привести в движение два камертона, которых полное созвучие слабо нарушено тем, что на верхнюю часть одного камертона наклеить по маленькому кусочку воска, отчего масса камертона несколько увеличится, движения его замедляются, а образуемые им волны становятся длиннее. Если один камертон производит 256 волн, а другой 257 или 255 волн (или вообще n и n ± 1 волн) в секунду, то каждую секунду будет происходить одно усиление и одно ослабевание тона, т. е. число дрожаний тона равно числу секунд. При разности чисел колебаний камертона или соответственных волн, равной 2, 3, 4 в секунду, произойдут 2, 3, 4 дрожания тона в секунду. Это явление дает возможность весьма точного сравнения камертонов между собой (см. Камертон). Оно замечается также при звучании струн и вообще при всех способах возбуждения музыкальных тонов, но для изучения явления лучше всего служат, кроме камертонов, еще органные трубы, из всех инструментов дающие наименее сложную волну [В 1888 г. лорд Рэлей остроумными приемами непосредственно показал явления И. и дифракции звука. Источником звука служил свисток, издававший чрезвычайно высокие, не слышимые ухом, звуки длиной волны от 5-20 мм; небольшая длина волн дала возможность получить явления И. во всей их чистоте, пользуясь даже небольшими отражающими поверхностями. Исследующим прибором служило чувствительное пламя, т. е. пламя газовой струи, выходящей под давлением из тонкого отверстия. Подобное пламя чрезвычайно чувствительно к высоким звукам; когда на него падает такая звуковая волна, оно опускается, раздваивается и начинает шипеть. Установив на некотором расстоянии от свистка отражающую звуковые волны стенку, Рэлей исследовал промежуточное пространство с помощью чувствительного пламени и заметил, что по мере удаления пламени от экрана к свистку поочередно наблюдаются места, в которых пламя вполне спокойно, и другие, в которых пламя опускается. Эти точки представляют узлы и пучности стоячих звуковых волн. С помощью подобного расположения приборов Рэлею удалось воспроизвести звуковые аналогии классических опытов Френеля — получения светлой точки в тени круглого диска и темной точки в середине светлого поля. Для первого опыта служил диск диаметром в 1 5 д.; длина волны звука была 6 мм; когда свисток стоял от диска на расстоянии 28 д., то пламя, поставленное против центра диска на расстоянии 10 д., приходило в сильные колебания (светлое пятно), которые делались слабее, когда диск убирали. Для второго опыта свисток и пламя располагались на расстоянии 116 стм., и в середине помещался экран с круглым вырезом в 20 стм. диам.; при действии свистка пламя оставалось спокойным (темное пятно), но сразу приходило в колебания, когда отверстие экрана уменьшали.].
И. в твердых телах. Волнообразное движение может быть возбуждено в веревке или струне, в которых также происходит отраженная волна, сочетающаяся с прямо идущей волной, вследствие чего образуются стоячие волны (Волны; см. также Колебательные движения). В пруте (напр. стеклянном) могут быть продольным трением возбуждены колебательные движения стоячих волн; образующиеся узлы и пучности могут быть различены в стеклянном пруте посредством поляризационного прибора. Стеклянная палочка при сильном звучании от натирания ее мокрыми пальцами может распадаться на цилиндрики вследствие недостаточной упругости материала.
И. жидких волн. Волны, образующиеся в жидкостях, также могут интерферировать между собой, производя различные явления, подобные тем, какие замечаются в звуковых волнах, а в том числе и стоячие волны. Их можно возбудить искусственно в воде, наполняющей продолговатый сосуд надлежащей длины, в котором волны, поднятые на одном конце сосуда и дойдя до другого его конца, отражаются от него и интерферируют с прямо идущими волнами (см. Волны). Волны в открытом водном пространстве могут то взаимно усиливаться, то ослабляться (см. там же); так называемый "девятый вал", идущий после нескольких меньших, обязан своим происхождением тоже И. Волны, отраженные от берега, то усиливают, то ослабляют прямо идущую волну, что в некоторых случаях (напр. приливы) представляет поразительное явление.
И. световых волн. Гюйгенс (1690) высказал гипотезу волнообразного движения эфира как основной причины явления света. Юнг (1802) развил доказательства в пользу этой гипотезы, которые, однако, все еще были весьма несовершенны. Френелю (1815) принадлежит заслуга прямого доказательства, что световые волны подлежат И., что слияние двух световых лучей может в известных случаях уничтожиться и произвести темноту. Знаменитый опыт И. света производится при употреблении прибора, известного под названием зеркал Френеля. Представим себе (фиг. 3) два небольших зеркала ОМ, ОМ 1, вырезанные из черного стекла, прикасающиеся ребрами [Собственно ребро прикосновения может и не образоваться, а вместо него -пересечение при мысленном продолжении плоскостей зеркал.], так что их поверхности почти составляют одну общую плоскость — по причине малой наклоненности одной к другой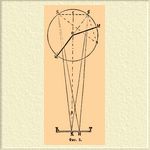
Фиг. 3.
Угол М'OМ между зеркалами на чертеже увеличен для ясности. Положим, что свет исходит из точки L [Буква L не вышла на чертежe; она должна стоять справа ниже M на точке пересечения двух линий, исходящих из S и S'.]; лучи света отражаются от зеркала МО по таким направлениям, как будто бы они исходили из точки S, находящейся за зеркалом в таком от него расстоянии, в каком L находится перед зеркалом (LS перпендикулярно к МО; ML = MS). Подобным образом лучи света отражаются от зеркальца М 1 О так, как если бы они выходили из точки S' (LS' перпендикулярно к ОМ') и пересекаются последней пополам. Пусть RТ изображает ширму, на которую падает свет, отраженный зеркалами, на ней точка К одинаково отстоит от точек SS', следовательно, световые волны, проходя пути равной длины, не представляют в точке К никакой разности хода (т. е. она равна нулю), а так как притом направления SK и S'K составляют между собой очень малый угол β (большой на чертеже для ясности), то происходит И. волн, а именно содействие их и соответственное усиление света в точке К. Но точки, лежащие от К вправо или влево по чертежу, уже не будут в равных расстояниях от S' и S; так, напр., расстояние S'H некоторой произвольной точки Н от S' больше SH — расстояния той же точки от S. Разность S'H — SH и соответственная разность хода волн, идущих вдоль этих линий, возрастают по мере удаления К от рассматриваемой точки Н; если эта разность для некоторого положения точки Н составит одну полуволну, то волны, вследствие И. противодействующие одна другой, взаимно уничтожатся и потому точка H не будет освещена. При дальнейшем удалении точки от К разность хода может достигнуть 2, 3, 4 и т. д. полуволн; при разности в 2 полуволны произойдет содействие волн и свет, при 3 полуволнах — темнота. Продолжая рассуждать таким образом, придем к заключению, что направо и налево от точки К будут расположены попеременно темные и светлые точки. Если в L будет находиться светящаяся линия (параллельная ребру соприкосновения зеркал, следовательно перпендикулярная к плоскости чертежа), то на ширме появятся светлые и темные линии (собственно полосы), проходящие параллельно ребру зеркал через точки К, Н и проч.; из них четные, считая от середины (0, 2, 4...) будут светлые, а нечетные — темные. Математическая обработка вопроса приводит к следующим согласующимся с опытом заключениям. 1) Полосы равно отстоят одна от другой; 2) их взаимные расстояния пропорциональны расстоянию ширмы от точек S и S'; 3) эти расстояния обратно пропорциональны расстоянию S'S между светящимися точками, следовательно, с уменьшением угла наклонения зеркал, а потому и с уменьшением и S'S полосы будут все более удаляться одна от другой и от центральной линии; 4) эти расстояния от центра явления различны для лучей разных цветов; будучи наибольшими для красных, наименьшими для фиолетовых и промежуточной величины для остальных цветов спектра, заключающихся между красными и фиолетовыми, они пропорциональны длинам волн. Из последнего заключения следует, что в ряду призматических цветов (см. Волны света) соответственные волны укорачиваются от красного к фиолетовому цвету. При белом и вообще сложном цвете точки L на ширме вместо полос одного какого-нибудь цвета появляются цветные полосы — род спектров, состоящих из ряда близких друг к другу узких полос от фиолетового до красного, причем фиолетовые края полос обращены к центральной полосе, которая одна остается белой, так как происходит от наложения полос всех цветов одной на другую. Из данных опыта можно определить числовую величину длины волны той или другой части спектра по формуле:
λ = 2 х tang β /n
Здесь λ обозначает искомую длину волны, x — расстояние полосы порядка n от центральной полосы, β — угол, которого место и значение видны из чертежа. Для этого основного для теории света опыта употребляется прибор из двух, как было сказано, черных зеркал, одно зеркало может при помощи микрометрического винта быть наклоняемо относительно другого. Перед зеркалами помещается источник однородного света; между ним и зеркалами находится непрозрачная пластинка (ширма) с щелью, параллельной ребру, которая соответствует светлой линии, о чем говорилось выше, при объяснении опыта. Величины 2х, т. е. расстояние между полосами одного порядка, из которых одна — направо, другая — налево от середины, измеряются посредством микрометрической лупы. Впрочем, измерения длины волн производятся обыкновенно не этим способом, а при помощи явлений дифракции, допускающих гораздо большую точность, так как там измеряемые величины гораздо больше (см. Дифракция). В опыте Френеля лучи света, исходившие из одного источника, были разделены посредством отражения от двух зеркал; лучи, отражавшиеся от каждого зеркала, исходили как бы от самостоятельного источника, казавшегося за зеркалом. Этот способ раздвоения одного источника не может быть заменен употреблением двух отдельных, действительно самостоятельных источников света. В каждом источнике беспрестанно происходят изменения не только в силе света, но и чрезвычайно быстрые изменения в направлениях колебаний эфирных частиц. Для успеха же опыта требуется, чтобы в интерферирующих волнах направления колебаний в каждый момент были одинаковы, чего невозможно достигнуть в двух отдельных источниках света (см. Свет, теория). В раздвоенном же источнике всякие перемены этого рода происходят одновременно в обеих частях. Зеркала Френеля обнаруживают явления И. только для небольших разностей хода, но некоторое изменение в вышеописанном приборе позволяет наблюдать явления И. и при разностях хода в несколько тысяч длин волн; для этой цели делают одно зеркало перемещающимся параллельно самому себе с помощью микрометрического винта, причем быстро увеличивается разность хода. Френель, кроме зеркал, пользовался еще стеклянной призмой с очень тупым углом, которая состоит из двух прямоугольных, склеенных малыми гранями призм с весьма острым углом (фиг. 4).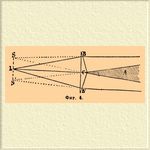
Фиг. 4.
Светлая щель L, параллельная ребрам призмы (следоват., перпендикулярная к плоскости чертежа), помещена в плоскости LC, нормальной к BB' и проходящей через С, ребро двойной призмы. Лучи, исходящие из L на двойную призму, преломляются в каждой ее половине и по выходе из них образуют два пучка расходящихся лучей, которых геометрические вершины будут S и S', лежащие на прямой, проходящей через точку L (собственно, только очень близко от нее). Ход лучей будет таков, как будто они вышли из названных двух точек, которые лежат тем ближе одна к другой, чем острее углы призм при В и В'. Угловое пространство А, покрытое на чертеже штрихами, содержит в себе лучи обеих систем и потому в нем произойдет явление И., подобное прежнему, т. е. появится ряд светлых и темных полос (каём), параллельных щели и ребрам призмы. Впоследствии Билье (Billet) и Бурбуз предложили еще новые приспособления для воспроизведения явлений И. и измерения длины волн. Билье пользовался выпуклой чечевицей, разрезанной пополам плоскостью, проходящей через главную оптическую ось; половинки стекла могли быть раздвигаемы одна от другой. Лучи, выходящие из светящейся щели, падая на поверхность разрезанного стекла, образуют в фокусе каждой половины изображение щели. Пучки света, идущие от этих двух изображений далее, образуют, подобно пучкам лучей в двойной призме Френеля, угловое пространство, общее им обоим, где и происходят явления И. Расстояние между двумя изображениями щели пропорционально расстоянию между половинками стекла; расстояние между каймами И. обратно пропорционально расстоянию между двумя изображениями, как и в предыдущих случаях. Бурбуз (Bourbouze), воспользовавшись зеркалом для отражения идущих из точки L лучей, принимает их на белую ширму RТ, освещенную, кроме того, непосредственно тем же источником света; обе системы лучей интерферируют между собой. На фиг. 5 LF и ЕК изображают лучи, падающие на зеркало MF и отраженные от него в точку К ширмы RT.
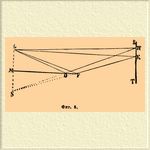
Фиг. 5.
Прямо идущий луч LK интерферирует с лучом FK. Подобно тому, другой отраженный луч ОН интерферирует с прямо идущим лучом LH; на ширме образуются каймы, как и в других случаях. Здесь надо рассматривать разность хода лучей, идущих из точек L и S, но, кроме того, надо принять во внимание изменение в направлении колебания эфирной частицы при отражении от зеркала, как от среды более плотной, чем воздух; пути SH и SK от этого отражения как бы укорачиваются на полволны (см. ниже и Свет, теория).
Цвета тонких пластинок. Явления И., искусственно вызываемые вышеописанными средствами, во многих случаях происходят и сами по себе. Старые оконные стекла, тонкий слой жирного масла, расплывшегося на спокойной поверхности воды, закаленная сталь и вообще поверхность металла, покрытая очень тонким слоем окисла другого металла, представляют игру цветов, которых происхождение, так же как и цветов мыльных пузырей, обязано И. света. Во всех перечисленных и других подобных им случаях — цвета появляются в тонких пластинках твердого тела, тонких слоях жидкости и воздуха. Для изучения этих явлений И. служат ньютоновы кольца — оптическое явление, обнаруживающееся в слое воздуха, заключающемся между поверхностями выпуклого и плоского стекол, наложенных одно на другое. В точке соприкосновения стекол и вокруг нее образуется темное пятно, окруженное концентрическими кольцами правильной круговой формы, попеременно светлыми и темными. При освещении однородным, напр. желтым, светом (пламя спирта, содержащего поваренную соль в растворе) кольца будут желтого цвета; при освещении же дневным светом каждое светлое кольцо состоит из нескольких сливающихся в одно колец различного цвета. Выпуклые стекла различной кривизны, наложенные на плоские, образуют кольца различных диаметров, но цвета и последовательность цветов в каждом кольце зависят единственно от порядка их, т. е. от номера кольца, считаемого от общего центра всех колец. Это дало повод составить нормальную шкалу из цветов ньютоновых колец, но употребление ее очень ограничено недостаточным разнообразием тонов. Расстояния между кольцами постепенно уменьшаются по мере удаления колец от центра или возрастания его номера; при дневном свете кольца высоких порядков почти вовсе незаметны, между тем как при однородном свете можно видеть много десятков колец до самой окружности чечевицы, но кольца по мере удаления от центра становятся все тоньше. При освещении одного и того же прибора светом разных цветов кольца одного и того же порядка имеют неодинаковый поперечник: красные кольца больше синих и фиолетовых, кольца промежуточных цветов имеют и промежуточной величины диаметр. Оттого цветные кольца высоких номеров, видимые при рассеянном свете, начинают налагаться краями друг на друга, при чем происходит смешение цветов и наконец составляется и белый цвет, т. е. кольца исчезают. Если выпуклое стекло будет приподнимаемо или нижнее опускаемо, медленно и на очень малые величины, то среднее темное пятно исчезает, а диаметры колец уменьшаются; с продолжением движения — кольца, приблизившиеся к центру, исчезают, а внешние кольца продолжают уменьшаться в диаметре, на месте же их образуются новые кольца. Эти движения объясняются так: каждому кольцу соответствует известная толщина слоя; если эта толщина увеличится, то бывшее на том месте кольцо подвигается ближе к центру, где слои воздуха тоньше. Наблюдая какую-нибудь точку в системе колец при пособии неподвижного значка, можно считать число проходящих колец. При освещении однородным желтым светом проходит при сказанном движении, как показал опыт, до 400 колец, а затем становятся неясными и при 500 исчезают почти совершенно, но опять появляются при 600 и становятся вполне отчетливыми при 1000. Дальнейшее увеличение расстояния между стеклами вызывает новое исчезание колец при 1500 и новое появление при 2000. Бунзенова газовая горелка с поваренной солью позволяет видеть 2 периода. Период прохождения 1000 колец сопровождается увеличением расстояния между стеклом на 0,289 мм; при надлежащем освещении [Эта периодичность происходит оттого, что желтый свет солей натрия не вполне однороден; его спектр состоит из двух желтых линий, хотя весьма близких между собой. Поэтому между стеклами происходит И. двух систем волн, которых длина очень мало различается между собой (см. выше И. звука).] таких периодов наблюдалось до 50. Зная эти соотношения, можно, обратно, по числу проходящих колец судить о величине перемещения стекла, и, как показал опыт, чувствительность подобного (см. Микрометры оптические, Фуко) измерительного прибора может дойти до 1/40000 мм. Лучший источник для такого рода опытов — смесь 4 частей древесного спирта и 1 части алкоголя, дающая слабый, но весьма чистый свет. Кольца во всех вышеописанных явлениях вообще очень узки, потому что толщина воздушного слоя между стеклами быстро изменяется, но если она останется постоянной на большой поверхности, то вся такая поверхность кажется окрашенной в один цвет, соответствующий толщине слоя. Помещая выпуклое стекло в вогнутое одинаковой кривизны, можно получить подобные цветные поверхности, которых цвет изменяется, смотря по степени нажатия одного стекла на другое. Подобным образом можно видеть значительные цветные поверхности в расщепленной слюде, в мыльных пузырях, на поверхности закаленной стали и т. п. Если между выпуклым и плоским стеклом впустить каплю жидкости, которой показатель преломления меньше, чем стекла, то кольца суживаются. Ниже говорится о способе вычисления толщины слоя воздуха в ньютоновых кольцах. Эти определения дают возможность определять толщину тонких пластинок по их цвету. Для этого надо отыскать в ньютоновых кольцах этот самый цвет и определить там толщину соответственного слоя.
Переходим теперь к измерительной части, после чего и можно будет объяснить участие И. в произведении цветов тонких пластинок. Фиг. 6 изображает плосковыпуклое стекло, лежащее на плоском стекле; h — толщина слоя воздуха в расстоянии r от точки соприкосновения стекол.
Фиг. 6.
Зависимость между этими величинами и величиной радиуса (R) кривизны стекла — следующая:
r2 = 2Rh, или r = (2Rh)1/2, или h = r2/2R.
Отсюда видно, что квадраты радиусов (следовательно, и диаметров) колец пропорциональны толщине соответственных слоев воздуха, которая может быть вычислена по измеренным r и R. Ньютон на основании сделанных им измерений нашел, что квадраты диаметров светлых колец (считая и среднее пятно), а следов., и толщина соответственных слоев относятся, как ряд четных чисел (0, 2, 4...), а квадраты диаметров темных колец относятся, как ряд нечетных чисел (1, 3, 5...) при нормальном падении освещающих лучей и при рассматривании колец со стороны падения лучей, т. е. в отраженном свете. Если смотреть со стороны плоского стекла, т. е. снизу, в проходящем свете, то и тогда видны светлые и темные кольца, но первые по своему месту соответствуют темным кольцам отраженного света, а вторые — светлым кольцам, видимым через отражение; в центре видно светлое пятно. Это в однородном свете. В случае более или менее косвенного освещения стекол квадраты диаметров колец увеличиваются пропорционально секансам углов падения (считая их от нормали). В случае замены воздуха жидкостями, имеющими показатель преломления меньший, чем показатель стекла, кольца суживаются; квадраты диаметров колец обратно пропорциональны показателям преломления. Происхождение цветных полос и колец объясняется следующим образом. Фиг. 7 изображает два плоские стекла M и М', параллельные между собой, и слой содержащегося между ними воздуха; S и S', суть параллельные лучи света, падающие на поверхность стекла М.
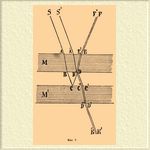
Фиг. 7.
Ход луча SА таков: AB - преломленная часть в стекле М, BC — часть, после того преломленная в воздухе, CD - отразившийся от стекла M' луч, DE — вновь преломившийся в стекле M луч, EF - вышедший из этого стекла луч. Кроме того, в точке D луч CD частью отражается по направлению DC' вниз и, пройдя путь C'D', выходит из стекла М' по направлению D'K'. Ход луча S'A' следующий: A'B' в стекле M и там же отраженная часть — В'E', выходящая в воздух по направлению E'F'; от точки В' часть луча идет также вниз по B'С"D"К". Волны, идущие по направлениям E'F, EF, параллельным и весьма близким или даже сливающимся между собой, интерферируют так же, как и по направлениям D'K', D"K" под стеклом М'. Луч SABCDE проходит путь, который на ВС + CD длиннее пути луча S'A'B'E'; предполагая, что лучи падают на стекло М почти нормально, можно принять ВС + CD равным двойной толщине воздушного слоя между стеклами, что обозначаем через 2 h. Но в точке С при отражении луча при переходе из воздуха в стекло теряется (или приобретается) полволны (λ/2), как было замечено выше (и как это объяснено в статье Свет, теория), следовательно, разность хода, которую нужно принять в расчет, равна 2 h + λ/2. Подобным образом разность хода волн в D"К" и D'К' равна 2 h + 2(λ/2), так как там происходят два отражения луча S — одно в С, другое — в D. Эти разности хода остаются неизменными для всего слоя воздуха, так как его толщина будет постоянной, следовательно, если 2h + λ /2 = 2n(λ/2), т. е. четному числу полуволн, то интерферирующие лучи дадут свет; при однородном свете, напр. красном, вся пластинка будет казаться красной в отраженном свете. В проходящем же свете разность хода, составляющая 2 h + 2(λ /2) = (2n + 1)(λ/2), — содержащая в себе нечетное число полуволн, сопровождается противодействием одних волн другим, и при равенстве их высоты, т. е. силы света, их взаимодействие произвело бы темноту. В действительности же произойдет только ослабление света, потому что обе системы волн, дойдя до точек D' и D", будут уже неравной силы вследствие неодинакового числа отражений. Так как длина оптических волн для красного цвета больше, чем для синего, то для окрашивания воздушного слоя в синий цвет надо бы пластинки сблизить между собой для той же числовой разности хода, и при освещении синим однородным светом. В случае освещения дневным светом воздушного слоя, имеющего толщину h, для И. волн, соответствующих составным частям белого света, будут существовать разные условия, так как разность хода, равная 2 h + λ/2, будет содержать в себе неодинаковое число полуволн, имеющих различную длину. Для некоторых волн может при этом произойти полное усиление света, для волн другой длины менее полное, а для иных даже более или менее полное уничтожение света. По этой причине цветной состав лучей после И. будет отличаться от состава их до И., отчего слой и получит окраску, зависящую от его толщины. Сюда относится опыт наложения вогнутого стекла на выпуклое, который был приведен выше. Если стеклянные плитки M и М' расположены будут наклонно одна к другой и соприкасаются ребром, толщина воздушного слоя между ними будет изменяться от нуля до некоторой величины h; поэтому при однородном свете появится ряд прямых темных и светлых каём, параллельных ребру соприкосновения, пластинок и равно отстоящих друг от друга. Наложение плосковыпуклого стекла на плоское дает систему концентрических колец, в которых расстояни
| "БРОКГАУЗ И ЕФРОН" >> "И" >> "ИН" >> "ИНТ" |
Статья про "Интерференция" в словаре Брокгауза и Ефрона была прочитана 1220 раз
| Креветки с газировкой |
| Креветки с газировкой |
TOP 15
- Волос
- Проно
- Степные животные
- Гимнастика
- Индийский океан
- Архитектура
- Сравнение, в литературе
- Манда
- Клитры
- Колесование
- Испарение
- Травоядные животные
- Оплодотворение у pacтений
- Вредные насекомые
- Электризация тел