


БНБ
"БРОКГАУЗ И ЕФРОН" (121188)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Интегрирование дифференциальных уравнений
Определение "Интегрирование дифференциальных уравнений" в словаре Брокгауза и Ефрона
Интегрирование дифференциальных уравнений (определение и разделение на категории — см. Дифференциальные уравнения) — общий вид обыкновенного дифференциального уравнения с одной независимой переменной х и с одной искомой функцией у от этой переменной есть
f(x, y, y', y"... y(n)) = 0... (*)
где функция f — некоторая заданная функция от n + 2 аргументов x, y, y', y". у (n), знаками у' у"... у (n) обозначен ряд последовательных производных искомой функции у, а знаком п — порядок дифференциального уравнения, т. е. порядок высшей производной. Интегрировать дифференциальное уравнение (*) это значит найти все возможные функции от одного переменного х, которые вместе с соответственными производными по подставлении взамен y, y', у"... у (n) в уравнение (*) обратили бы его в тождество. Задача И. обыкновенного дифференциального уравнения некоторого порядка с одной неизвестной функцией есть задача неопределенная, что видно было уже в ст. Интегральное исчисление, при И. простейшего уравнения первого порядка y' = f(x), общее решение которого есть
у = ∫f(x)∙dx + C
и которое заключает произвольную постоянную C; это замечание относится к уравнениям какого угодно порядка. Самым общим решением уравнения (*), его так называемым общим интегралом, будет функция вида
y = F(х, С 1, C2...С n)
где C1, C2.Cn некоторые произвольные постоянные, независимые друг от друга. Всякое решение, которое получается из общего от подстановки вместо постоянных произвольных некоторых частных численных значений, называется частным решением или частным интегралом данного дифференциального уравнения. Эйлеру принадлежит в высшей степени важное замечание, развитое потом Лагранжем и другими математиками, о существовании у некоторых дифференциальных уравнений так назыв. особенных решений, которые не могут быть получены из общего интеграла через подстановку вместо постоянных произвольных некоторых численных значений, а получаются, считая постоянные произвольные некоторыми функциями от х. Отсюда видно, что задача И. дифференциальных уравнений с одной неизвестной функцией от одной независимой переменной приводится к нахождению: во-первых, общего интеграла, а во-вторых, — всех особенных решений.
Пpимеpы: 1. Интегрировать уравнение первого порядка:
ху' — у = 0;
написав это уравнение в виде
x.dy — у.dx = 0
или dy/y = dx/x
и интегрируя обе части, находим
∫dy/y = ∫dx/x.
Откуда lg y = lgx + lgC
или y = C.x
2. Общий интеграл уравнения у" = у есть y = С 1ex + C2e-x.
3. Для примера особенных решений рассмотрим геометрическую задачу: найти кривую, касательная к которой была бы в постоянном расстоянии а от начала координат.
Уравнение касательной, проведенной через какую-нибудь точку (х, у) кривой, есть
У — y = y'(X — x).
Дифференциальное уравнение вопроса представляется в виде
(у — у'х)/(1 + y'2)1/2 = a
или y = y'.x + а(1 + у' 2)1/2... (1)
Дифференцируя относительно x, получим уравнение:
0 = dy'[x + ay'/(1 + y'2)1/2]
которое разлагается на два
dy' = 0 и х + ay'/(1 + y' 2)1/2 = 0.
Из первого находим:
y' = C.
Oткуда на основании (I):
у = С.х + а(1 + С 2)1/2... (2)
Из второго находим:
x = -ay'/(1 + y'2)1/2... (3)
Внося это в ур. (1), получим:
y = a/(1 + y'2)1/2... (4)
Возвысив в квадрат и сложив уравнения (3) и (4), будет:
x2 + y2 = а 2... (5)
Уравнение (2) представляет общий интеграл и выражает бесчисленное множество прямых, отстоящих от начала координат в расстоянии а; все эти прямые касаются окружности, определяемой уравнением (5), которое есть особенное решение заданного дифференциального уравнения.
Из немногочисленных классов обыкновенных дифференциальных уравнений, приемы интегрирования которых известны, особенного внимания заслуживают так называемые линейные уравнения. Общий их вид есть
Xoy(n) + X1y(n-1) + ... + Xn-1y' + Xny = Y
где Хо, Х 1. Х n-1, Xn и Y суть некоторые заданные функции независимого переменного х. Если коэффициенты Хо, Х 1 . Хп суть постоянные, то линейное уравнение называется уравнением с постоянными коэффициентами; что касается функции Y, то, какова бы она ни была, линейное уравнение с постоянными коэффициентами всегда интегрируется в квадратурах.
Остановимся на интегрировании линейных уравнений с тем, чтобы обратить внимание на весьма важный прием, употребляемый при И. дифференциальных уравнений, развитый Лагранжем и называемый изменением произвольных постоянных (la variation des constantes arbitraires). Этот прием впервые встречается уже в теории Луны Эйлера и ныне имеет обширное применение в "небесной механике".
Начнем с интегрирования линейного уравнения с постоянными коэффициентами, но без последнего члена, т. е. в которых Y = 0. Таким образом, пусть задано уравнение
aoy(n) + a1y(n-1) + ...+ an-1y' + any = 0 ... (A)
Для интегрирования такого уравнения находят сперва п независимых решений этого уравнения у 1, у 2. у n, тогда общий интеграл уравнения (А) выразится формулой
y = С 1 у 1+ C2y2 +... + С n у n
Что касается частных решений у 1, y2 . уп, то для линейного уравнения с постоянными коэффициентами они могут быть представлены в виде ek.x, где k - корень уравнения
а okn + а 1kn-1 +...+ an-1k + an = 0 ... (В)
Если заданные коэффициенты a о , a1. ап таковы, что это алгебраическое уравнение имеет п различных корней k1, k2. kn, то за п различных решений заданного линейного уравнения без последнего члена (А) могут быть приняты функции  так что общий интеграл будет иметь вид:
так что общий интеграл будет иметь вид: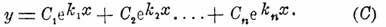
В случае, если уравнение (В) имеет менее чем п различных корней, т. е. если некоторые корни этого уравнения одинаковые (кратные), то форма общего интеграла уравнения (C) несколько видоизменяется, причем все-таки общий интеграл выражается функцией линейной и однородной относительно постоянных произвольных C1, C2... Сп. Отсюда видно, что каковы бы ни были коэффициенты заданного линейного уравнения (А), его общий интеграл выразится формулой:
у = С 1 у 1 + С 2y2 +... + С nyn ... (D)
где y1, y2... у n некоторые найденные уже функции от х.
Обратимся теперь к И. уравнений с постоянным членом, т. е. такого, которое отличается от ур. (А) тем, что во второй части вместо нуля стоит некоторая функция от х. Общий его вид будет
aoy(n) + a1y(n-l) + ... + а n-1y' + а ny = Y... (Е)
Покажем, что решение ур. (Е) можно представить в виде ур. (D), в котором значение y1y2...yn останется прежнее (частные решения уравнения без последнего члена), a C1, C2...Cn уже не постоянные, а некоторые функции от х. Выражаясь иначе, мы будем изменять (варьировать, считать переменными) постоянные, находящиеся в общем интеграле уравнения без последнего члена так, чтобы вышел общий интеграл уравнения с последним членом. Имея в виду, что нужно удовлетворить только одному уравнению (Е), переменных же постоянных имеется много, n для упрощения задачи всегда можно предписать ряд новых условий, так, напр., можно потребовать, чтобы, кроме условия, что функция (D) есть решение уравнения с последним членом, все производные до порядка n- 1 включительно выражались одинаковыми формулами, как в случае С 1, С 2...С n постоянных, так и в случае переменных.
Если C1, C2...C п переменные, то, дифференцируя уравнение (D), получим:
y' = C1y'1 + C2y'2 +... + С ny'n + С' 1 у 1 + С' 2 у 2 +... + С' n у n.
Чтобы у' выражалось одинаково, как в случае С постоянные, так и в случае С переменные, необходимо положить:
С' 1y1 + C'2 у 2 +... + С' nyn = 0 ... (F1)
Тогда очевидно
y' = C1 у' 1 + С 2y'2 +...+ Cny'n ... (G1)
Подобным образом, чтобы вторые производные в обоих предположениях выражались одинаково, необходимо на основании дифференцирования уравнения (G 1) положить:
C'1y'1 + C'2y'2 +... + С 'n у' n = 0... (F2)
тогда будет
y" = C1y1" + С 2y2" +...+ С nyn"... (G2).
Продолжая далее до (n -1)-й производной включительно, получим
С' 1y1(n-1) + С' 2y'2(n-1) +... + С' nyn(n-1) = 0... (Fn-1)
и у(п-1) = C1y1(n-1) + C2y2(n-1) +...+ Сп y п (n-1) ... (Gn-1).
Что касается n -й производной, то она уже не будет одна и та же в двух предположениях и в случае С переменных представится в виде:
y(n) = C1y1(n) + С 2y2(n) +... + Спуп (n) + С' 1 у 1(n-1) + C'2y2(n-1) +... + C'nyn(n-1) ... (Gn).
Умножая уравнения (G n), (Gn-1)... (G1) и (D) соответственно на ao, a1,. an-1, an и складывая, найдем, что уравнение (Е) представится так:
ao(C'1y1(n-1) + C'2y2(n-l) +. + С' n у n(n-1)) + С 1 (а o у 1(n) + а 1y1 (п-1) +... + any1) + C2(aoy2(n) + a1y2(n-1) +... + any2) + Cn(aoyn(n) + а 1yn (п- 1) +... + а ny п) = Y.
Так как у 1 y2 . уп не какиe-нибудь функции, а, как замечено уже выше, суть частные решения линейного уравнения без последнего члена, то легко видеть, что последнее уравнение обращается в
С 1y1(n-1) + C'2y2(n-1) +. + C'nyn(n-1) = Y/ao ... (Fn).
Уравнения (F 1), (F2). (Fn) суть линейные первой степени относительно n неизвестных С' 1, C'2... С' n все коэффициенты этих уравнений — известные, вполне определенные функции от x, ибо функция Y задана, а функции у 1, у 2... у n уже найдены. Решая эту систему n уравнений первой степени относительно С' 1, C'2 ... С' n по правилам элементарной алгебры, получим:
C'1 = φ 1(x)
C'2 = φ 2(x)
...
...
C'n = φ n(x).
А после И. будет:
C1 = ∫1 (х)dх + Г 1
C2 = ∫2(x)dx + Г 2
...
...
С n = ∫n (х) dx + Г n.
Если подставить эти выражения для C1 C2 ... Cn в уравнение (D), то получится и окончательный общий интеграл линейного уравнения с последним членом, именно:
y = Г 1y1 + Г 2y2 +.+ Г n у n + y1∫1(x)dx + y2∫2(x)dx +...+ у n∫n(x)dx
Изменение произвольных постоянных как прием для И. применяется в тех случаях, когда заданное уравнение или систему уравнений интегрировать непосредственно весьма затруднительно, но можно, откидывая некоторые члены, получить новые уравнения такого вида, что можно написать их самые общие решения. Изменяя затем постоянные величины, входящие в эти решения, подбирают эти постоянные так, чтобы удовлетворились первоначально заданные уравнения.
В механике встречается надобность интегрировать системы так назыв. обыкновенных совокупных уравнений. Пусть задана система.
f1 (x, у, z... u, у', z'... и', y", z"...) = 0
f2(x, y, z... u, y', z'... u', y", z"...) = 0
.
fk (x, у, z... u, у', z'... u', у", z"...) = 0.
В эти уравнения входят: независимая переменная х, n ее пока произвольных функций у, z.u и ряд производных от этих функций по независимой переменной х первых или высших порядков. Такая система называется системой k обыкновенных совокупных уравнений с n неизвестными функциями. Если n < k, то, вообще говоря, системе нельзя будет удовлетворить выбором n искомых функций и она будет возможна лишь при существовании некоторых условий, которым должны удовлетворить функции f1, f2 ... fk. Если n > k, то некоторые из функций будут совершенно произвольны. Самый важный случай представляется при п = k, т. е. когда число уравнений равно числу искомых функций. Этот случай обыкновенно и рассматривается. Если система не содержит противоречий, то интегрировать ее — значит найти все возможные значения искомых функций, обращающие ее в тождество, другими словами, чтобы в искомом выражении этих функций через независимую переменную входило достаточное число произвольных постоянных независимых друг от друга. Каков бы ни был порядок каждого из уравнений системы, т. е. порядок, наибольший из порядков производных, входящих в эти уравнения, всегда можно, вводя новые искомые функции и увеличивая за то число уравнений системы, получить систему m уравнений с m неизвестными функциями первого порядка, т. е. систему, в которой, кроме независимой переменной х и искомых функций, войдут только первые от них производные по х. Сделать это весьма просто, принимая за новые функции производные от прежних до порядка на единицу меньше наибольшего порядка производной от соответствующей функции, входящей в рассматриваемую систему. К такого рода системам принадлежат системы, названные Якоби каноническими и к которым приводятся уравнения различных задач в механике. — Интегрирование всякой системы m уравнений с m неизвестными функциями m -ого порядка может быть приведено или к интегрированию одного уравнения m -ого порядка с одной неизвестной функцией или к интегрированию нескольких обыкновенных уравнений, из которых каждое заключает одну неизвестную функцию, сумма порядков которых равна m.
И. дифференциальных уравнений с частными производными. Основное отличие уравнений с частными производными от уравнений обыкновенных заключается в тех произвольных элементах, которые вводит их И.; именно при И. уравнений с частными производными приходится рассматривать такие решения, которые содержат произвольные функции от независимых переменных. Пусть дано уравнение
x(du/dx) + y(du/dy) +. + t(du/dt) = n. (1)
где n некоторое постоянное число, а и — искомая функция от m независимых переменных х, у,. t. Так как в уравнение (1) входят частные производные только первого порядка, то такое уравнение называется уравнением с частными производными первого порядка в отличие от уравнений с частными производными высших порядков. Если некоторые функции
a1 = y/x, a2 = z/x ... am-1 = t/x
удовлетворяют все уравнению
x(da/dx) + y(da/dy) + z(da/dz) +. + t(da/dt) = 0
и если положим
и = xn. П(a 1, а 2 . а m-1)... (2)
то легко заметить, что какова бы ни была функция П от m — 1 аргументов a1, a2 . am-1, заданное уравнение (1) удовлетворится выражением (2), в которое входит совершенно произвольная функция П. В этом состоит известная теорема Эйлера об однородных функциях.
Для примера возьмем уравнение колебания струны
d2 и/dy 2 - a2(d2u/dx2) = 0;
легко проверить, что этому уравнению удовлетворяет следующая функция от и:
и = П(х + ау) + Ф(х — ay)
где П и Ф совершенно произвольные функции.
Что касается теории уравнений с частными производными, то благодаря трудам Коши, Якоби и их последователей довольно обстоятельно разобраны уравнения первого порядка. Теория же уравнений высших порядков в настоящее время находится еще в зачаточном состоянии. Известно весьма мало общих свойств таких уравнений, и все сводится к разбору уравнений частного вида (отдельные примеры); впрочем, для математической физики весьма важно и то, что уравнения линейные относительно частных производных какого угодно порядка с постоянными коэффициентами интегрируются, как это показал Коши, при помощи интегралов Фурье.
Геометрическое значение И. обыкновенных дифференциальных уравнений между независимой переменной х и ее функцией у состоит в том, что отыскиваются все кривые F(x), обладающие некоторым общим свойством, выражаемым заданным дифференциальным уравнением. Отсюда ясно, что в уравнения искомых кривых должны входить произвольные постоянные, выбором которых можно отличить одну из кривых от всех прочих, принадлежащих к рассматриваемой системе. Аналогичное значение имеют для пространства дифференциальные уравнения с частными производными между независимыми переменными х и у и их искомой функцией z. Интегрировать такое уравнение значит найти все поверхности, обладающие общим свойством, выражаемым заданным уравнением. При интегрировании таких уравнений, понятно, должны входить произвольные функции, ибо из числа различных поверхностей можно выбирать не только такие, которые проходили бы через конечное число произвольно заданных точек пространства, но и такие, которые проходили бы через произвольно заданные кривые в пространстве. — Хотя задача интегрирования дифференциальных уравнений есть задача весьма трудная и удается лишь для малого числа простейших классов уравнений, тем не менее, интегральное исчисление является могущественным орудием натуральной философии, потому что строка Тейлора дает возможность разлагать решение дифференциального уравнения в ряды, расположенные по степеням независимого переменного, и получать таким образом приближенное значение искомых функций независимо от того, умеем ли мы интегрировать заданное дифференциальное уравнение или нет. Блестящие примеры такого рода приближенного И. представляет небесная механика, где при рассмотрении движений небесных тел, притягивающихся между собой по законам Ньютона, уже в случае трех тел (Солнце, Земля и Луна или Солнце, комета и возмущающая планета) является знаменитая задача о трех телах, которая до сих пор представляет непреодолимые затруднения, быть может, по существу, а может быть, только по сравнительной сложности относящихся сюда дифференциальных уравнений. Нечего говорить уже о задаче более общей, когда рассматривается движение более чем трех тел и которая имеет, однако, место в астрономии. Предсказание небесных явлений, открытие новых светил при помощи теоретических исследований (открытие Нептуна), обстоятельное разъяснение различных особенностей в движении их (неравенства) — все это свидетельствует о том, что если приемы приближенного И. дифференциальных уравнений и далеки от желательной степени теоретического совершенства и представляют в настоящее время область, где еще многое нужно сделать, однако интегрирование уравнений, по крайней мере в приложениях к физическим наукам, представляет часть математики, наиболее важную и богатую новыми результатами.
Д. Граве.
| "БРОКГАУЗ И ЕФРОН" >> "И" >> "ИН" >> "ИНТ" |
Статья про "Интегрирование дифференциальных уравнений" в словаре Брокгауза и Ефрона была прочитана 2956 раз
| Коптим скумбрию в коробке |
| Буддийская молитва в Камбодже |
TOP 15
- Волос
- Проно
- Степные животные
- Гимнастика
- Индийский океан
- Архитектура
- Сравнение, в литературе
- Манда
- Клитры
- Колесование
- Испарение
- Травоядные животные
- Оплодотворение у pacтений
- Вредные насекомые
- Электризация тел