


БНБ
"БРОКГАУЗ И ЕФРОН" (121188)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Двучлен
Определение "Двучлен" в словаре Брокгауза и Ефрона
Двучлен (мат.) — В добавление сказанного в ст. Бином (см.) заметим по поводу бинома Ньютона. Уже Вьетту было известно, что от возвышения Д. а + b в какую угодно целую положительную степень n получается формула вида
(1) (а +b) n = а n + P1an—1b1 + P2an-2b2 +... + Р n—1аb n—1 + bn,
где в правой части многочлен, состоящий из n+1 членов. В каждом из них сумма показателей над а и над b равна n. Кэффициенты же Р 1, Р 2,... Р n — суть некоторые целые числа. Ньютон первый показал закон составления этих коэффициентов. Коэфф. Р k оказывается равным числу сочетаний из n предметов по k (см. Сочетания), или, выражая это формулой
(2) Pk = [n(n—1)...(n-k + 1)]/1.2.3...k
Уже Ньютон, а за ним и все остальные математики, между прочим Эйлер, рассматривали формулу, приведенную выше, также и для n дробных и отрицательных. В этих случаях (а + b)n представляется уже не в виде многочлена с n+1 членами, а в виде бесконечного ряда, начинающегося с членов
а n + Р 1an—1b + Р 2а n-2b2 +...,
причем Р k вычисляется по формуле (2) и может не быть целым числом. Бесконечные ряды употребляются лишь в том случае, когда эти ряды суть так назыв. сходящиеся (см. Ряд). Полагая b/a = х, мы приходим к рассмотрению выражения (1+x) m или, другими словами, к нахождению суммы ряда
1 + (n/1)x + {[n(n—1)]/1·2}x2 + {[n(n—1)(n-2)]/1·2·3}x3 +...
для всех значений х и n действительных или мнимых, для которых ряд сходящийся. Полное решение послднего вопроса представляет знаменитая работа норвежского математика Абеля: "Recherches sur la série 1 + (m/1)х +... (см. журнал Crell'я, т. I, 1826). Ограничиваясь вещественными значениями х и m, замечаем, что формула
(1+x)n = 1 + nx + {[n(n—1)]/1·2}x2 +...
1) при n целом и положительном справедлива, каково бы ни было значение х;
2) при n не равном целому и положительному числу имеет место при —1 < х < +1;
3) при х = +1 имеет место, когда m > —1;
4) при х = — 1 имеет место, когда m > 0.
Бином Ньютона дает возможность вычислять корни по приближению. Например: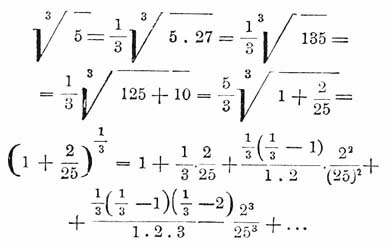
Вычисляя только написанные четыре члена, мы получим для 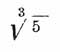 число 1,70997858, в котором верны пять знаков после запятой.
число 1,70997858, в котором верны пять знаков после запятой.
Д. Граве.
| "БРОКГАУЗ И ЕФРОН" >> "Д" >> "ДВ" >> "ДВУ" |
Статья про "Двучлен" в словаре Брокгауза и Ефрона была прочитана 1127 раз
| Буддийская молитва в Камбодже |
| Буддийская молитва в Камбодже |
TOP 15
- Волос
- Проно
- Степные животные
- Гимнастика
- Индийский океан
- Архитектура
- Сравнение, в литературе
- Манда
- Клитры
- Колесование
- Испарение
- Травоядные животные
- Оплодотворение у pacтений
- Вредные насекомые
- Электризация тел