


БНБ
"БРОКГАУЗ И ЕФРОН" (121188)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Двойные ряды
Определение "Двойные ряды" в словаре Брокгауза и Ефрона
Двойные ряды
Двойные ряды
(мат.). — Бесконечные ряды, каждый член которых представляет из себя сумму некоторого сходящегося бесконечного ряда, суть так называемые Д. ряды или ряды с двумя входами (sériés à double entrée), a потому Д. ряды суть ряды вида 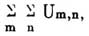 , где m и n суть два целых числа, служащих для указания соответственного члена U m,n Д. ряда. Суммирование производится как по значку m, так и по значку n для целых значений чисел m и n, лежащих в некоторых границах. Обыкновенно (так, например, в теории эллиптических функций) рассматриваются ряды, состоящие из бесчисленного множества членов, причем суммирование распространяется на всевозможные положительные и отрицательные целые значения чисел m и n. Возьмем в плоскости систему прямоугольных координат ху; затем для каждого члена Um,n ряда укажем точку, имеющую координаты x = m, у = n. Все подобные точки, соответствующие ряду, лежат в углах сетки, образованной прямыми линиями, проведенными на расстоянии единицы друг от друга параллельно осям х-ов и у-ов. Если ряд расположен по положительным и отрицательными значениям чисел m и n, то точки, соответствующие его членам, могут заполнять всю плоскость. Подобные ряды будут сходящимися, когда сумма членов, соответствующие точки которых расположены внутри некоторой замкнутой кривой какого угодно вида, стремится к определенному пределу, когда контур фигур раздвигается в бесконечность по всем направлениям. Д. ряды играют видную роль в теории эллиптических функций.
, где m и n суть два целых числа, служащих для указания соответственного члена U m,n Д. ряда. Суммирование производится как по значку m, так и по значку n для целых значений чисел m и n, лежащих в некоторых границах. Обыкновенно (так, например, в теории эллиптических функций) рассматриваются ряды, состоящие из бесчисленного множества членов, причем суммирование распространяется на всевозможные положительные и отрицательные целые значения чисел m и n. Возьмем в плоскости систему прямоугольных координат ху; затем для каждого члена Um,n ряда укажем точку, имеющую координаты x = m, у = n. Все подобные точки, соответствующие ряду, лежат в углах сетки, образованной прямыми линиями, проведенными на расстоянии единицы друг от друга параллельно осям х-ов и у-ов. Если ряд расположен по положительным и отрицательными значениям чисел m и n, то точки, соответствующие его членам, могут заполнять всю плоскость. Подобные ряды будут сходящимися, когда сумма членов, соответствующие точки которых расположены внутри некоторой замкнутой кривой какого угодно вида, стремится к определенному пределу, когда контур фигур раздвигается в бесконечность по всем направлениям. Д. ряды играют видную роль в теории эллиптических функций.
Д. Г.
| "БРОКГАУЗ И ЕФРОН" >> "Д" >> "ДВ" >> "ДВО" |
Статья про "Двойные ряды" в словаре Брокгауза и Ефрона была прочитана 1100 раз
| Шотландский Стовис |
| Шотландский Стовис |
TOP 15
- Волос
- Проно
- Степные животные
- Гимнастика
- Индийский океан
- Архитектура
- Сравнение, в литературе
- Манда
- Клитры
- Колесование
- Испарение
- Травоядные животные
- Оплодотворение у pacтений
- Вредные насекомые
- Электризация тел