


БНБ
"БРОКГАУЗ И ЕФРОН" (121188)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Гиперболические функции
Определение "Гиперболические функции" в словаре Брокгауза и Ефрона
Гиперболические функции — По аналогии с тригонометрическими функциями Sinx, cosx, определяемыми, как известно, при помощи Эйлеровых формул
sinx = (exi — e—xi)/2i, cosx = (exi + e—xi)/2
(где е есть основание нэперовых логарифмов, a i = √[-1]); иногда вводятся в рассмотрение так называемые Г. функции sinhypx, coshypx. Эти функции определяются при помощи уравнений
sinhyp x = (ex — e—x)/2, coshyp x = (ex + e—x)/2.
Название Г. эти функции получают от того, что их можно выводить из рассмотрения равносторонней гиперболы (см. Гипербола), как тригонометрические функции получаются из круга. Возьмем круг радиуса = 1 и равностороннюю гиперболу с полуосью, равной единице. Проведем в гиперболе оси ОА и OB и точно так же в круге возьмем два взаимно-перпендикулярных диаметра. Начиная от точки А на круге и на гиперболе, возьмем дуги АС такие, чтобы площади соответственных секторов ОАС (см. чертежи) равнялись некоторому числу z.
Черт. 3.
Из конца дуги С опустим перпендикуляр CD на диаметр OA. Тогда получим следующее: в круге длина дуги АС будет равна, очевидно, 2z, ибо площадь сектора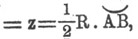
но R = 1; CD для круга будет sin2z, a OD будет cos2z. Подобным же образом для гиперболы OD будет coshyp2z, a CD будет sinhyp2z. Обозначая OD через х, CD через у, мы получим уравнение круга в виде
x2 + y2 = 1,
а уравнение гиперболы в виде
x2 — y2 = 1;
отсюда мы замечаем, что между гипербол. функциями должно существовать соотношение
coshyp2x — sinhyp2x = 1,
аналогичное с тригонометрическим
cos2x + sin2x = 1.
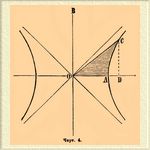
Черт. 4.
Кроме того, можно вводить функцию
tghypx = sinhypx/coshypx.
Теорема сложения Г. функций аналогична с соответственной теоремой тригонометрических. Эта теорема выражается формулами:
sinhyp(x + y) = sinhypх ×coshypy + coshypx× sinhypу
и
coshyp(x + у) = coshypx × coshypу — sinhypx ×sinhypy.
Д. Гp.
| "БРОКГАУЗ И ЕФРОН" >> "Г" >> "ГИ" >> "ГИП" >> "ГИПЕ" |
Статья про "Гиперболические функции" в словаре Брокгауза и Ефрона была прочитана 1375 раз
| Коптим скумбрию в коробке |
| Панайпай |
TOP 15
- Волос
- Проно
- Степные животные
- Гимнастика
- Индийский океан
- Архитектура
- Сравнение, в литературе
- Манда
- Клитры
- Колесование
- Испарение
- Травоядные животные
- Оплодотворение у pacтений
- Вредные насекомые
- Электризация тел