


БНБ
"БРОКГАУЗ И ЕФРОН" (121188)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Гидродинамика
Определение "Гидродинамика" в словаре Брокгауза и Ефрона
Гидродинамика — Т. называется та часть теоретической механики, которая имеет целью нахождение общих законов движения жидкостей. первыми исследованиями относительно движения жидкостей были опытные исследования Торичелли, которые привели его к открытию известного закона, что скорость истечения жидкости из малого отверстия в сосуде равняется скорости, приобретаемой телом, свободно упавшим с той высоты, какую имеет уровень жидкости в сосуде над отверстием. Открытие это было опубликовано в 1643 г. Двадцать лет спустя, Вариньон предложил Парижской академии наук тот теоретический вывод этого закона, который и до сих дор встречается в элементарных сочинениях. В 1687 г. Ньютон, в первом издании книги "Philos. naturalis principia mathematica", дал также теоретический вывод того же закона, но этот вывод представляет собой одно из неудачных мест его знаменитой книги, несмотря на исправление, сделанное во втором издании ее. Первая попытка теоретического вывода общего закона движения жидкости была сделана Даниилом Бернулли, который в 1738 г. напечатал трактат под заглавием: "Hydrodynamica, sive de viribus et motibus fluidorum commeutarii"; в нем Д. Бернулли, на основании закона сохранения живой силы, вывел известную и имеющую важное значение в гидравлике формулу, выражающую, что при установившемся течении тяжелой несжимаемой жидкости напор между положениями двух каких-либо частиц одной и той же линии тока равняется приращению высоты скорости. Несмотря на это, первые основания Г. еще не были установлены, и те, которые стали работать далее по пути, проложенному Даниилом Бернулли, а именно Маклорен и Иван Бернулли, дальнейших успехов не имели. Только после открытия начала д'Аламбера оказалась возможность установить Г. на прочном основании. Сам д'Аламбер показал ("Essai d'une nouvelle Th éorie sur la ré sistance des fluides", 1752), что от уравнений равновесия жидкости можно перейти к уравнениям движения их, если заменить приложенные силы потерянными; но полученные д'Аламбером уравнения оказалось возможным упростить и обобщить. В 1755 г. Эйлер ("Principes g énéraux du mouvement des fluides", "Hist. d e l'Acad. de Berlin", 1755; "De principiis motus fluidorum", "Novi Comm. Acad. Petrop.", т. 14, 1759) получил дифференциальные уравнения движения жидкости под следующим видом: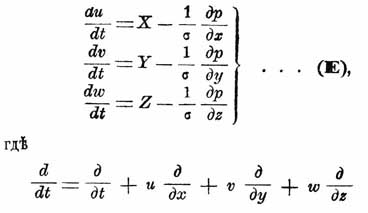
где
d/dt = d/dt + ud/dx + vd/dy + wd/dz,
p есть давление, σ плотность, и, v, w — проекции на оси координат скорости в точке жидкости, находящейся в момент t в точке пространства, определяемой координатами x, y, z; X, Y, Z суть проекции (на оси координат) рассчитанной на единицу массы внешней силы в той же точке жидкости. К этим уравнениям. заключающим пять искомых функций (u, v, w, р, σ) от t и координат x, у, z, должно присоединить еще так называемое "уравнение неразрывности":
d σ /dt + d(σ u)/dx + d(σ v)/dy + d(σ w)/dz = 0
и уравнение, выражающее зависимость между плотностью и давлением. Эти дифференциальные уравнения относятся к так называемым совершенным, идеальным жидкостям, не оказывающим никакого сопротивления срезывающим или тангенциальным силам, иначе говоря, к жидкостям, не обладающим внутренним трением. В случае применения этих уравнений к "несжимаемым" жидкостям, должно считать плотность σ постоянной величиной; тогда уравнение неразрывности принимает вид:
du/dx + dv/dy + dw/dz = 0
выражая несжимаемость жидкости. В случае применения к газообразным веществам, сохраняющим постоянную температуру во всех частях массы, зависимость между давлением и плотностью принимается, по закону Бойля, следующей:
p = k σ,
где к — постоянная, зависящая от природы газа. Если же предполагается, что движение газа совершается при условии сохранения того же количества тепла в каждом малейшем элементе объема газа, то зависимость между p и y предполагается такой:
p = К σγ,
где γ = 1,41 для воздуха. Кроме этих уравнений, которые должны быть удовлетворены во всякой точке жидкости, должны быть удовлетворены еще особые условия в точках поверхности жидкости.
Лагранж в своей "M é canique analytique" придал другую форму дифференциальным уравнениям гидродинамики. При составлении дифференциальных уравнений в форме (Е) скорости u, v, w (а также p и σ) рассматриваются как функции от t и от координат x, у, z точек пространства, занимаемых точками жидкости в момент t; при составлении же Лагранжевых уравнений координаты x, y, z точек жидкости в момент t рассматриваются как функции от t и от координат a, b, c той же точки в начальный момент t = 0. Лагранжевы уравнения имеют следующий вид: первое
(d2x/dt2)(dx/da) + (d2y/dt2)(dy/da) + (d2z/dt2)(dz/da) + (1/ σ)(dp/da) = X(dx/da) + Y(dy/da) + Z(dz/da)... (L)
и два другие, отличающиеся от первого тем, что во втором входят частные производные по b, в третьем — по с. Уравнение неразрывности имеет также иной вид.
Впоследствии оказалось, что и эта форма дифференциальных уравнений гидродинамики также впервые указана Эйлером, хотя за нею установилось наименование Лагранжевой. Теория интегрирования дифференциальных уравнений не дает еще средств получить решения дифференциальных уравнений ни формы (Е), ни формы (L) в общем виде; возможно получить решения их только в некоторых простейших специальных случаях. В таких случаях по преимуществу пользуются Эйлеровой формой, когда решение требуется отыскать; но иногда обращаются и к уравнениям Лагранжа, в особенности тогда, когда представляется возможным угадать вид функций от t, а, b, с, выражающих x, y, z.
Специальные категории случаев, в которых оказывается возможным решить уравнения гидродинамики, принадлежат преимущественно к тем, в которых внешние силы имеют потенциал или силовую функцию и в которых течение жидкости невихревое, то есть скорости u, v, w имеют потенциал, так что
u = d φ /dx, v = d φ /dy, w = d φ /dz
где φ есть функция от x, y, z, t. К числу таких вопросов относятся вопросы о течении жидкости в двух измерениях, о распространении волн, о движении твердых тел в жидкостях. Кроме этого рассмотрены некоторые вопросы о движении вихревых нитей и колец.
В 1822 г. Навье, а затем в 1845 г. Stokes дополнили уравнения гидродинамики членами, зависящими от внутреннего трения или вязкости жидкости. Вслед за тем Stokes, Гельмгольц, Мейер и др. рассмотрели некоторые вопросы о движении твердых тел в жидкостях, обладающих внутренним трением. У нас, в России, гидродинамику обогатил своими исследованиями проф. Н. Е. Жуковский; в особенности интересны две большие работы его в этой области: "О движении твердого тела, имеющего полости, наполненные однородной капельной жидкостью", в журнале "Русского Физико-Химического общества" за 1888 г. (том XVII) и "Видоизменение метода Кирхгофа для определения движения жидкости в двух измерениях при постоянной скорости данной на неизвестной линии тока" в XV томе "Математического Сборника" (1890). Из трактатов по гидродинамике следует указать на следующие: Н. Lamb, "A treatise on the mathematical theory of the motion of fluids" (1879), A. Basset, "A treatise on hydrodynamics" (1888); G. Kirchhoff, "Vorlesungen über math ematische Physik, Mechanik" (1876) и на неоконченные еще изданием лекции по гидродинамике проф. Жуковского (1886).
Д. Бобылев.
| "БРОКГАУЗ И ЕФРОН" >> "Г" >> "ГИ" >> "ГИД" >> "ГИДР" |
Статья про "Гидродинамика" в словаре Брокгауза и Ефрона была прочитана 1829 раз
| Семга на горелке |
| Семга на горелке |
TOP 15
- Волос
- Проно
- Степные животные
- Гимнастика
- Индийский океан
- Архитектура
- Сравнение, в литературе
- Манда
- Клитры
- Колесование
- Испарение
- Травоядные животные
- Оплодотворение у pacтений
- Вредные насекомые
- Электризация тел