


БНБ
"БРОКГАУЗ И ЕФРОН" (121188)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Гармонические движения
Определение "Гармонические движения" в словаре Брокгауза и Ефрона
Гармонические движения
простые и составные. Представим себе, что по кругу радиуса а (на черт. 1 изображен круг, имеющий центр в О) движется точка N с постоянной скоростью в сторону, указанную стрелкой, причем полный оборот по окружности она совершает в течение времени Т.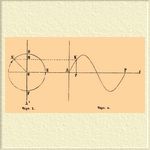
Чертеж 1. Чертеж 2.
Проекция M точки N на направление прямой Х 1 ОХ будет тогда совершать вдоль по ней, вверх и вниз, колебательное движение, называемое простым гармоническим движением и выражаемое следующим уравнением:
x = asin(2 π t/T) (I)
если считать время от того момента, когда точка N была в С, а положительные расстояния х по прямой X1OX считать по направлению ОХ.
Если же считать время от какого-либо другого момента, то это же движение выразится уравнением:
x = asin(2 π t/T- ε ) (II)
где е есть фаза, или эпоха, гармонического колебания, а — амплитуда и Т — период, или продолжительность, двойного качания точки М.
На черт. 2 движение, выражаемое уравнением (I), изображено графически. От точки А по прямой At откладываются длины, пропорциональные временам t; так, длина АР изображает время Т , а длина Ар — время, в течение которого движущаяся по кругу точка перешла из С в N на черт. 1. Затем от каждой точки, такой как р, откладывают ординату рК, равную соответственному расстоянию ОМ. Построенная кривая будет синусоида; на черт. 2 изображена только часть ее, соответствующая одному полному периоду и представляющая одну волну кривой.
Два или несколько прямолинейных гармонических движений по одной и той же прямой, около того же центра, того же периода, но различных амплитуд и разных фаз, соединяются в одно простое гармоническое движение того же периода. Если а 1, а 2, а 3, ... суть амплитуды составляющих гармонических движений, а ε 1, ε 2, ε 3, ... — их фазы, то квадрат амплитуды составного простого гармонического движения будет равен:
α 2 + β 2,
a тангенс фазы этого движения равен отношению β к α, где α и β суть следующие суммы:
α = a1cos ε 1 + a2cos ε 2 +.
β = a1sin ε 1 + a2sin ε 2 +.
Из соединения нескольких простых Г. движений различного периода по одной и той же прямой получаются сложные прямолинейные гармонические движения, а из соединения двух простых Г. движений, совершающихся по двум взаимно перпендикулярным или наклонным одна к другой прямым, получаются криволинейные Г. движения. На черт. 3 графически представлено сложное прямолинейное Г. движение, выражаемое уравнением:
x = sin ω t + sin2 ω t,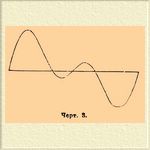
Чертеж 3
а на черт. 4 — другое сложное Г. движение, выражаемое уравнением:
x = sin2 ω t + sin(3 ω t + 3 π / 8), где ω = 2 π /T.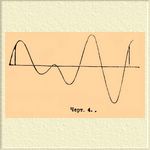
Черт. 4
При соединении двух простых Г. движений различных соизмеримых периодов движущаяся точка описывает кривые линии, называемые кривыми Лиссажу. Полную теорию Г. движений можно найти в "Treatise on natural philosophy by T homson and Tait" (Vol. I. Part I, kinematics).
Гармоническое отношение. Понятие о Г. отношении введено древними геометрами. Папп в своей книге "Математический сборник" говорит, что три числа находятся в Г. отношении, если отношение первого к третьему равно отношению разности первого без второго и третьего; такое отношение названо Г. потому, что оно встречалось в теории музыки древних.
Две точки a и а 1 делят длину bс в Г. отношении, если длины ас, аа 1 и ab находятся в Г. отношении, т. е.:
ac/ab = (ac — aa1)/(aa1 — ab), или
ac/ab = -(ac — aa1)/(ab — aa1) (III)
или
ab/ac: a1b/a1c = — 1.
Гармоническому отношению между тремя длинами ас, аа 1, ab можно придать еще следующий вид:
2/aa1 = 1/ab + 1/ac
что нетрудно получить из (III). Г. отношение играет важную роль в высшей геометрии; см. Chasles "Trait é de géometrie supérieure".
Гармонические сферические функции. Под именем spherical harmonie functions английские физико-математики подразумевают однородные функции V от х, y, z, удовлетворяющие дифференциальному уравнению:
d2V/dx2 + d2V/dy2 + d2V/dz2 = 0
См . Сферические функции.
Д. Б.
Гармонические движения отдельной частицы происходят под влиянием силы, направленной к положению равновесия частицы и изменяющейся прямо пропорционально расстоянию ее от него. Подобного рода силы возникают при растяжении, сжатии, сгибании упругих тел, при отклонении гибкой натянутой струны из ее положения равновесия и во многих подобных случаях. Поэтому гармоническое движение встречается в природе очень часто: все звуковые колебания, каковы колебания камертонов, струн и т. п. представляют гармоническое движение. Качания маятника при малых размахах, сравнительно с длиной его, происходят по тем же законам. Вследствие пропорциональности движущей силы расстояниям тела от положения равновесия гармоническое движение обладает замечательным свойством — изохронностью колебаний, т. е. продолжительность периода движения одинакова и при больших и при малых амплитудах колебания. По этой причине одно и то же звучащее тело (камертон, струна и т. п.) издают всегда тон одной и той же высоты, хотя и различной силы (тихий или громкий) в зависимости от силы удара. Продолжительность периода гармонического колебания (Т) зависит исключительно от ускорения (k) на расстоянии единицы длины (1 см) от положения равновесия движущихся частиц, именно
T = 2 π: √k
Ускорение же движения пропорционально двигающей силе и обратно пропорционально двигаемой массе. Этим и пользуются на практике: при настройке музыкальных инструментов изменяют натяжение струн; для изменения скорости хода карманных часов изменяют длину пружинки маятника и т. д.
Ф. д. Ф.
| "БРОКГАУЗ И ЕФРОН" >> "Г" >> "ГА" >> "ГАР" >> "ГАРМ" |
Статья про "Гармонические движения" в словаре Брокгауза и Ефрона была прочитана 1487 раз
| Бургер двойного помола |
| Луковый соус |
TOP 15
- Волос
- Проно
- Степные животные
- Гимнастика
- Индийский океан
- Архитектура
- Сравнение, в литературе
- Манда
- Клитры
- Колесование
- Испарение
- Травоядные животные
- Оплодотворение у pacтений
- Вредные насекомые
- Электризация тел