


БНБ
"БРОКГАУЗ И ЕФРОН" (121188)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Вес и взвешивание.
Определение "Вес и взвешивание." в словаре Брокгауза и Ефрона
Вес и взвешивание. — Изложение этой статьи разделено на следующие части: 1) вес, удельный вес, плотность; 2) взвешивание, точное взвешивание, общие приемы, частные способы; 3) взвешивание в воде, или гидростатическое, для определения плотности твердых и жидких тел; 4) разновес, или гири для взвешивания.
1) Bсе тела притягиваются друг к другу и, следовательно, к Земле; тела, находящиеся над поверхностью Земли и ничем не поддерживаемые, падают на нее, а поддерживаемые — производят давление на подставку. В первом случае сила притяжения измеряется ускорением при падении тел, во втором — весом их; скорость падения и ускорение тел не зависят от величины тел, хотя в целом теле содержится вдвое более вещества, чем в его половине, и масса целого тела вдвое более массы его половины. Нет средств измерять непосредственно количество вещества, содержащегося в телах, тем не менее, нельзя сомневаться, что эти количества в телах одного состава пропорциональны массам и весам тел (в одном и том же месте Земли). В кубическом дециметре меди содержится вещества в 1000 раз больше, чем в одном куб. см, а также масса и вес первого в 1000 раз больше массы и веса второго. Кубич. см платины имеет вес, одинаковый с весом 2,42 куб. см меди; на этом основании допускают, что и количества вещества, содержащегося в куб. см платины и в 2,42 кубич. см меди, одинаковы (см. ниже — плотность). Практическая цель взвешивания заключается в сравнении количеств вещества, содержащегося в разных телах. Однако вес тела непостоянен, будучи тем менее, чем на большем расстоянии от Земли (от ее центра) тело находится; вес на полюсе и вообще в полярных странах более, чем на экваторе, как по причине сжатости Земли при полюсах и потому большей близости тел к центру Земли, так и по причине центробежной силы, противодействующей земному притяжению на экваторе сильнее, чем в полярных странах. Взвешивание на обыкновенных весах с коромыслом не может служить для доказательства этой изменяемости веса, потому что вес гирь изменяется в одинаковом отношении с весом тел. Только пользуясь пружинными весами, если б они могли быть достаточно чувствительными при большой нагрузке, можно было бы в этом убедиться; но другая мера притяжения — ускорение — подлежит более удобному измерению; качаниями маятника (см. Притяжение, Маятник) доказано, что земное притяжение (а следовательно, и вес) в разных местах Земли неодинаково. Если установить весы на башне, и уравновесить какое-нибудь тело гирями, а потом, опустив его на проволоке в нижний этаж башни, снова уравновесить гирями, положенными на другой чашке весов, находящихся наверху, то окажется, что вес тела меньше внизу (хотя и немного), чем наверху (опыт Жолли в 1881 г.).
Итак, вес тел есть непостоянная величина, даже на поверхности Земли, но постоянна масса тела; ускорение подвержено тем же изменениям, как и вес. Обозначая буквою р вес тела, буквою g — ускорение и буквою m — массу тела, имеем следующее соотношение между этими величинами:
р = тg.
Для другого тела, которого вес есть Р и масса М будет
Р = Мg
так как ускорение g остается прежним. При взвешивании употреблены будут гири, которых вес и масса будут также р, m, Р и M, т. е.
р:Р = т:М.
В другом месте земли р, Р и g обратятся в p', Р' и g', но массы не переменятся: значит, опять
р':Р' = т:М.
Отсюда видно, что хотя вес и есть непостоянная величина, но взвешиванием тел достигается цель: сравнение количеств вещества и масс тел между собою. Давления на чашку весов зависят от массы тела, в смысле количества вещества, и потому вес есть мера давления, производимого массою тела, изменяющаяся при переходе от одной широты к другой, при переходе от одной местности к другой, лежащей выше или ниже первой. Вес зависит и от других нижепоименованных обстоятельства. Так, для очень точных взвешиваний надо принять в соображение, что вес всякого тела в пустоте больше, чем в воздухе. Тело, которого объем равен 1 куб. дециметру, теряет в сухом воздухе при показании барометра 760 мм столько, сколько весит вытесненный телом кубический дм такого воздуха, т. е. 1, 293 грамма. Чем больше плотность атмосферного воздуха (показываемая высотою ртутного столба в барометре), тем значительнее эта потеря; чем влажнее воздух, тем она менее. Для сообщения гирям (разновескам) необходимого в этом отношении постоянства — на них пишется вес их в пустоте. Так как вновь делаемые гири сравниваются взвешиванием со старыми, то все равно, в какой бы широте это ни делалось. Вес в пустоте называется истинным и для некоторой местности имеет постоянную величину; кажущийся вес в воздухе зависит от давления воздуха, от влажности и еще от температуры, влияющей и на плотность воздуха, и на объем самого тела, а, следовательно, и вытесняемого им воздуха.
Удельный и относительный вес и плотность суть величины, связанные с весом тел. Определения этих терминов не всегда однообразны: можно принять следующие.
Относительный вес тела показывает отношение истинного веса его к истинному весу воды такого же объема, при некоторых второстепенных условиях, касающихся температуры; по этому определению относительный вес есть отвлеченное число.
Удельный вес есть истинный вес единицы объема тела, имеющего температуру 0°. Температура упоминается потому, что от нее зависит количество вещества, помещающегося в определенном объеме. Итак, удельный вес выражается именованным числом.
Плотность тела зависит от количества вещества, помещающегося в определенном объеме. Так, в кубическом дециметре вмещается некоторое количество воздуха, имеющего упругость 760 мм, а при двойном давлении или упругости, но при той же температуре, это количество удвоится. Если этот воздух охладить, то он, сжимаясь, дает доступ новому количеству воздуха, так что все количество вещества в прежнем объеме увеличится; от нагревания же воздуха, при свободном его выходе, оно уменьшилось бы. Понятия об этих изменениях получаются посредством взвешивания. Сравнение количеств вещества платины и меди, вмещающихся в 1 куб. см при 0°, менее ясно, так как вещества разнородны. Если держаться мнения, что атомы всех тел одинаковы весом и объемом, то, если бы они находились в состоянии покоя, все вещества были бы тождественны (Грэм — Graham, 1866). Но каждый атом обладает известным движением, которым обуславливается занимаемый им объем; чем быстрее это движение, тем значительнее нужный для атома объем. Поэтому вещества отличаются одни от других только плотностью. С такой точки зрения можно говорить о различном количестве вещества в куб. см платины и меди, и потому различие в весе их будет указывать на различное уплотнение вещества в платине и меди. Плотность тел будет обратно пропорциональна объемам, нужным для основных атомов и пропорциональна их числу, следовательно, плотность тел пропорциональна весу тел при одинаковых объемах и других второстепенных условиях. Вес одного куб. см воды при наибольшем ее сжатии (4°С) равен 1 грамму, а весь 1 куб. см ртути при 0° равен 13,6 грамма; эти числа условным образом выражают количества вещества и, следовательно, плотность воды и ртути. Плотность ртути относительно воды выражается отвлеченным числом 13,6, а плотность воды будет 1. Можно еще принять, что именованные числа выражают абсолютные, а отвлеченные — относительные плотности; во всяком случае по одинаковости чисел для них нет опасности от смешения обоих понятий. Это удобство исчезает при переходе к другой системе мер. Например, один куб. дюйм воды наибольшей плотности весит 3 зол. 66 долей, а куб. дюйм ртути — 50 зол. 23 доли: второе число более первого в 13,6 раза. Относительная плотность при всяких мерах, конечно, выражается одним и тем же числом, но абсолютная плотность — различными. То же самое можно сказать про относительный вес и удельный вес.
Из вышесказанного видно, что хотя понятие плотности отличается от понятия веса, так как последний служит только измерителем плотности, но числа для них одни и те же в метрической системе. Вследствие этого безразлично употреблено терминов относительный и удельный вес. и плотность; смешения понятий при этом не произойдет, если придерживаться метрической системы мер, так как из дела всегда видно, идет ли речь о плотности, как о свойстве, измеряемом числом, или же об отношении веса тел, как об отвлеченном числе, нужном для сравнения. Впрочем, понятие о плотности не исчерпывается сказанным.
Взвешивание есть процесс сравнения веса различных тел между собою, состоящий из многих частных приемов, заканчиваемый и исправляемый путем вычислений во всех случаях, требующих большой научной точности. В таких случаях руководятся точными понятиями о весе тел, в которых не нуждается практика обыкновенного торгового или хозяйственного В. Даже аптекарское В. и определение веса благородных металлов, драгоценных камней — все эти случаи сравнительно точного взвешивания не нуждаются в научных тонкостях, которые проистекают из научных понятий о весе. Во всех случаях, ведущих к обыденной житейской цели, для определения веса какой-нибудь вещи кладут эту вещь на одну чашку весов, а на другую чашку накладывают столько гирь, сколько понадобится для равновесия весов, о чем можно судить по положению указателя, при крепленного к коромыслу весов (см. Весы). Само собою разумеется, что степень чувствительности и верности весов, а также точности гирь должны соответствовать роду практических В., для которых они назначаются. Вследствие простых требований практической жизни и манипуляции соответственных В. очень просты. Совсем другое представляет взвешивание с научною целью, когда надо принять в расчет влияние на вес тел температуры, плотности и влажности окружающего воздуха и, наконец, влияние сфероидальности земли и ее вращения на оси, что объяснено выше.
Ф. Петрушевский.
2) Точное взвешивание. — С большою точностью можно взвешивать только вполне не изменяемое в отношении веса тело, т. е. негигроскопичное (не притягивающее паров воды), не сгущающее газов в порах, не испаряющееся, или защищенное от изменений на время взвешивания помещением в легкие стеклянные или иные сосуды, закрытые или даже запаянные. Но так как гигроскопичность стеклянной поверхности может еще произвести ощутительную погрешность при взвешивании, то в химических работах тигли с осадками после прокаливания должны быть охлаждены в аппарате для высушивания (эксикатор) или под колоколом воздушного насоса. Часто стараются осушить воздух в ящике весов; однако это может повести к новой погрешности, о чем сказано ниже. Всякое взвешивание требует сопоставления двух определений положения равновесия коромысла, поэтому недостаточна чувствительность весов, а необходимо постоянство их показаний (см. Весы), Если, например, стрелка отклоняется на 1/10 деления от перевеса в 0,01 мг, то при повторениях в определении положения равновесия можно ожидать разницы даже в пять раз большей, т. е. в 0,05 мг; это последнее число и определит точность отсчета. Увеличивая чувствительность весов повышением гайки, назначенной для установки центра тяжести коромысла, можно и xopoшиe весы сделать непостоянными, и наоборот, понижая чувствительность, можно достигнуть постоянства и в посредственных весах. С понижением центра тяжести коромысла уменьшается и время его колебаний, а потому взвешивание идет скорее. Быстрота колебаний при достаточной чувствительности и составляет главное достоинство новых аналитических весов с коротким коромыслом, заставляющее предпочитать их весам с длинным коромыслом. Смотря по цели взвешивания, те или другие причины погрешностей получают преобладающее влияние. В. делаются или для сравнения масс тел между собою или для их определения в абсолютной мере, напр. в граммах. К первому разряду относятся взвешивания для химических анализов, когда ищут процентный состав тела, также для определения плотности тел и вообще все случаи относительных измерений, когда результат выражается отвлеченным числом. Второй же разряд обнимает все взвешивания для определения объемов тел по его весу (собственно массе) и плотности, также те химические анализы, которыми определяют массу вещества в единице объема жидкости, взвешивание при калориметрических и вольтаметрических опытах, а также определение веса с целью вычисления моментов инерции.
Обращаясь теперь к рассмотрению приемов точного взвешивания, следует указать степень важности разных предосторожностей и поправок. Весы должны быть установлены прочно, на полочке, прикрепленной к стене комнаты, если пол ее деревянный или вообще такой, что через него передаются толчки от движения людей. Для устранения потоков воздуха, мешающих правильности колебаний коромысла, весы покрываются ящиком — футляром со стеклами; во время заканчивания взвешивания ящик должен быть закрыт. Но этой предосторожности мало для самых точных взвешиваний: дыхание наблюдателя, лучеиспускание его тела, близость газовой горелки — все это может вызвать течения воздуха в ящике или несимметричное и неравномерное изменение коромысла. Если чувствительность весов есть 1/10000000 (см. Весы), то изменение длины одного плеча на такую же часть будет сопровождаться ошибкой во взвешивании, равной чувствительности. Для латунного коромысла такое удлинение произойдет при нагревании на 1/18°, для более чувствительных весов разность температур обоих плеч коромысла в 1/100° могла бы произвести при взвешивании ошибку около 1/5000000 взвешиваемого груза; при взвешивании одного килограмма ошибка составила бы около 1/5 мг. В международном бюро мер и весов в Париже весы установлены на особых фундаментах в зале, которой стены поддерживаются при постоянной температуре, наложение малых гирек совершается посредством особых механизмов; взвешиваемое тело кладется на весы и приблизительно уравновешивается за сутки до окончательного взвешивания; положение равновесия наблюдается с помощью зрительных труб с расстояния 4 метров.
Взвешивание производят следующими способами: а) положив взвешив. тело на одной чашке весов, кладут гири на другую до приведения коромысла в горизонтальное положение; б) производят два взвешивания: первое как сейчас было сказано и второе — после перекладки взвешиваемого тела на ту чашку, где в первый раз были разновески и уравновешивания гирями на той чашке, где прежде было тело (это способ Гаусса); в) уравновешивают тело не разновесками, но тарою, т. е. какими-нибудь грузами, металлическими обрезками, опилками, и потом, сняв тело, уравновешивают тару разновесками (это способ Борды); г) на одну чашку весов кладут наибольшее количество гирь, выдерживаемое весами без повреждения, и уравновешивают ее тарою на другой чашке; затем кладут взвешиваемое тело (весящее менее наибольшего груза) на чашку, где гири и оставляют разновесок столько, сколько В. нужно для приведения коромысла к равновесию. Это способ взвешив. при постоянной нагрузке.
Во всех этих способах, описанных в частности ниже, главные приемы собственно приведения в равновесие остаются одни и те же. Положив тело на одну чашку весов при поднятом арретире (см. Весы), накладывают гири (сперва крупные) на другую, для чего захватывают их щипчиками или особыми вилками; затем, опустив арретир, смотрят, много ли или мало гирь положено, и сближают пределы систематическими пробами, кончая сантиграммами. Тогда уже опускают стеклянную стенку ящика и накладывают на коромысло "ездока" (фиг. 13) в 1 сантиграмм.
Фиг. 13.
Когда стрелка станет делать приблизительно равные размахи в обе стороны от средней черты шкалы, не превышающие одного деления, можно считать, что равновесие достигнуто. Такой прием взвешивания при хороших весах достаточен, когда можно довольствоваться точностью в один миллиграмм. Если же требуется закончить взвешивание со всей точностью, допускаемой данными весами, то наблюдают качания стрелки для вычисления из них положения, которое она примет при равновесии и остановке качаний. Положим, что деления шкалы пронумерованы слева направо; пусть крайнее положение стрелки налево будет против a1 делений, крайнее правое на а 2, и опять налево а 3. По правилу Гаусса, положение равновесия стрелки на шкале а вычислится из следующей формулы:
a = (a1 + 2a2 + a3)/4.
При выводе этой формулы отброшены малые величины высшего порядка. Если обозначить буквою п отношение величин двух последовательных, понемногу убывающих размахов а 2 и а 1 стрелки, то ошибка при вычислении по этой формуле будет только
(1/8)(a2 — a1)(1 — n)2
Повторив такое же наблюдение и вычисление, когда к разновескам прибавлен 1 миллиграмм, получим новое положение равновесия а'; а' — а будет мерою чувствительности весов при данной нагрузке от добавки одного миллиграмма. Определив тем же приемом положение равновесия а 0 ненагруженных весов, вычисляют прибавку δ к весу гирь, положенных при первом наблюдении, по формуле:
δ = (a 0 — a)/(a' — a).
При взвешивании качаются не только коромысло, но обыкновенно и чашки; надо останавливать маятникообразные колебания последних, так как переменная центробежная сила, развивающаяся этими колебаниями, обыкновенно не остается при больших грузах без влияния на коромысло. Употреблением способа качаний исключается влияние на положение равновесия трения призмы о ее подставку, которое, одинаково уменьшая размахи направо и налево, не влияет прямо на определяемое равновесие коромысла. Однако трениe в современных весах так незначительно, а потеря времени при наблюдениях по способу колебаний так велика, что способы непосредственного наблюдения равновесия обыкновенно предпочитаются в обыденной практике. В этом отношении воздушные успокоители весов (см. Весы) представляют весьма интересное, хотя и мало еще испытанное нововведение. См. Весы Кюри (см. Весы и фиг. V табл. А).
ВЕСЫ. Табл. А.
V. Воздушный успокоитель.
Было упомянуто, что вес тела в воздyxе изменяется от многих причин; поэтому после точного взвешивания в воздухе надо вычислить вес тела в пустом пространстве. Означая буквами Р и D истинный вес и плотность взвешиваемого тела, а через р и d — истинный вес и плотность гирь, уравновешивающих это тело, и через q — вес куб. см воздуха, в котором произведено взвешивание, можно выразить равенство обоих давлений, предполагая, что плечи коромысла равны, следующею формулою:
P(1 — q/D) = p(1 — q/d)
Решая уравнение и отбрасывая члены с малой величиной q2 и еще высшими степенями q, получим
P = p(1 + q/D — q/d)
Вес куб. см воздуха q при содержании в нем 0,04% углекислоты, давлении атмосферы Н, упругости содержащегося в нем водяного пара h и температуре t, составляет:
q = [1,293052(H — 0,3779h)]/[(1 + 0,00367t)76] мг.
Для устранения сложной поправки на потерю веса в воздухе иногда помещают весы в безвоздушное пространство и особыми механизмами накладывают гири на чашки и снимают их. Но при этом обнаружилось, что ребра призм, лишенные в пустоте слоя сгущенного на их поверхности воздуха, стали давать большое трение и скоро тупились.
Влияние потери веса гирь в воздухе на результат взвешивания вполне исключается при определении отношения весов двух тел, если воздух не изменился во время взвешивания. Положим, что для двух взвешиваемых тел, имеющих плотности D и Dl и уравновешенных гирями р и р 1, составлены выражения:
P(1 — q/D) = p(1 — q/d)
и
P1(1 — q/D1) = p1(1 — q/d).
Разделяя первое на второе имеем:
[ Р/P 1][(1 — q/D)/(1 — q/D1)] = p/p1
Если еще и плотности D и D1 равны или мало отличаются между собою, то влияние воздуха исключается вполне и тогда
P/P1 = p/p1.
При обыденных химических анализах пренебрегают поправкой на вытесненный воздух, не опасаясь сделать большой ошибки. Рассмотренный способ взвешивания требует равноплечего коромысла. Заметим, что влияние неравенства плеч коромысла само собою исключается при всех относительных взвешиваниях, если только тело всегда кладется на одну и ту же чашку весов. В других случаях пользуются одним из способов b, c, d, перечисленных и упоминаемых ниже.
b) Способ Гаусса заключается в двух взвешиваниях: 1) тело находится на левой чашке, гири — на правой, и 2) тело находится на правой чашке, а гири — на левой. Если длину левого плеча обозначим через l1 a длину правого через l2, вес гирь на правой чашке через р 2, а на левой — через р 1, то имеем равенства статических моментов:
Pl1 = p2 l2 и Pl2 = p1 l1 откуда Р = √p 1 p2.
Так как р 1 и p2 мало различны, то √p1 p2 мало отличается от 1/2(p1 + p2).
Из тех же выражений можно определить отношение между длинами плеч коромысла, а именно:
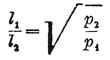 , или приблиз. l1/l2 = 1 + [(p2 — p1)/(2p1)].
, или приблиз. l1/l2 = 1 + [(p2 — p1)/(2p1)].
c) Способ Борды совершенно нагляден: тело уравновешивают тарою вместо гирь, затем снимают его и заменяют гирями; значит, тело и гири действуют поочередно на одно и то же плечо. Вес тела, очевидно, равен весу гирь в воздухе; отсюда вычислением находят вес тела в пустом пространстве. Способы Борды и Гаусса суть способы двойного взвешивания, хотя обыкновенно этим названием обозначают способ Борды.
d) Взвешивание всегда на одном плече при постоянной нагрузке коромысла имеет достоинства двойного взвешивания и сопровождается одною и тою же постоянной чувствительностью весов, которая, впрочем, есть наименьшая из всех возможных для этого коромысла, потому что относится к наибольшей нагрузке коромысла. О таком взвешивании упоминается в иллюстрированном каталоге физических приборов Саллерона и, кажется, еще ранее Бокгольцем, устроившим даже особенные весы для этой цели. В сочинении Д. И. Менделеева "Об упругости газов" (1875 г.) изложены доводы в пользу этого способа.
3) Взвешивание гидростатическое, или взвешивание тел в воде и вообще в каких-нибудь жидкостях, служит для определения плотности или относительного веса твердых и жидких тел. Относительный вес выражается числом, равным отношению веса тела к весу воды равного объема. Если тело опущено в воду, то его вес кажущимся образом уменьшается на величину веса воды равного объема (Архимедов закон); вследствие этого разность веса тела в воздухе (точнее — в пустоте) и в воде есть вес воды равного с погруженным телом объема. Разделяя первый вес на второй, получим число, измеряющее относительный вес тела. Полученные таким образом числа не будут достаточно точны для научных целей; необходимо еще делать вычисления, принимая во внимание истинный вес тела, полагая, что вытесненный объем воды равен объему тела при 0°, и что температура воды есть 4°С. — Для взвешивания в воде необходимо бывает повесить тело на проволоку или поместить его в подвешенный сосуд, если оно в порошке или, если оно легче воды и поэтому всплывает. Назовем через q' вес гирек, уравновешивающих в воздухе эту проволоку или сосуд, на весах с плечами l и l'. Пусть объем тела, данного для исследования, будет V куб. см; искомую плотность его, при температуре опыта t°, отнесенную к воде при температуре 4°, обозначим через Х t, а плотность воды при той же температуре — Δ t. Уравновесив в воздухе подвешенное на одной стороне В. тело с проволоками-гирями Q на другой стороне, получим уравнение:
V(Xt — q)l = (Q — q')(1 — q/d)l' (I)
где q вес куб. сантиметра воздуха, a d плотность гирь. Подставляют под весы сосуд с водою так, чтобы в нее погрузилось все тело и часть поддерживающей его проволоки и удаляют приставшие пузырьки воздуха (что при простых и порошкообразных телах иногда бывает очень трудно и требует предварительного кипячения или помещения в разреженном воздухе). По диаметру и длине погруженной части проволоки вычисляют ее объем: каждый куб. миллиметр будет соответствовать потере в один миллиграмм; обозначим эту величину буквою q". Уравновешивая погруженное тело с проволокою-гирями Q', получим новое уравнение;
V(Xt — Δ t)l = (Q' — q' + q")(1 — q/d)l' (II).
Решая совокупность уравнений I и II получим:
Xt = [ (Δ t — p)][(Q — q')/(Q — Q' — q")] + q (III).
Отношение плеч коромысла само собою исключается, другие же сокращения мы вправе сделать только в предположении, что при всех взвешиваниях вес куб. см воздуха остается тот же. Для определения плотности жидкостей употребляется несколько способов. По одному из них надо определить вес какого-нибудь твердого тела в воздухе, в воде и в испытываемой жидкости. В этом случае берут обыкновенно стеклянный запаянный шарик, нагруженный налитою ртутью настолько, чтобы он тонул. Шарик подвешен на платиновой проволочке; пользуясь теми же обозначениями, что и раньше, получим.
в воздухе V(Xt - q)l = Q(1 — q/d)l' (IV)
в воде V(Xt - Δ t)l = Q'(1 — q/d)l' (V)
в жидкости V(Xt - Yt)l = Q"(1 — q/d)l' (VI).
Из уравнений IV, V и VI получим:
Yt = [(Q — Q")(Q — Q')][ Δ t — r] + r ... (VII), стр.
Оба уравнения III и VII выражают плотность тела при температуре опыта, отнесенную, однако, к воде при ее наибольшей плотности (4°С). Когда известен коэффициент расширения тела k, нетрудно вычислить его плотность при температуре 0°. Действительно, масса тела, равная произведению его объема на плотность, останется постоянною, поэтому:
XtV0(1 + kt) = X0V0
или
X0 = Xt(1 + kt).
В химическо-технической практике часто приходится определять плотность жидкостей, чтобы узнать их состав и степень чистоты; для такой цели употребляются одноплечие весы Мора, усовершенствованные Руманом, Вестфалем и друг. (см. Весы). Вес гирек, уравновешивающих тело в жидкости, будет равен ее плотности (без поправок на воздух), если за единицу веса этих гирек будет взята потеря веса этого тела в воде при определенной температуре. Таким образом вполне обходятся без нежелательных для практиков вычислений. Чтобы упростить манипуляции, гирькам придают вид "ездоков" весом в 1, 0,1, 0,01 и 0,001 и вешают их прямо на коромысло, снабженное нарезками на каждой десятой доле своей длины. Руман придает погруженному телу, содержащему в себе термометр, объем в 5 куб. см и вес в 15 г; оно вполне уравновешивается в воздухе коротким плечом коромысла; в случае поломки этого тела его можно заменить другим, не переделывая всего набора разновесок. Капиллярные силы, действующие с переменным напряжением и направлением, в месте выхода проволоки из жидкости, не позволяют сделать гидростатическое взвешивание достовернее, чем до 0,001 г. Поэтому-то ученые и потратили столько труда на изобретение разных методов определения плотности жидкостей. Реньо ввел в употребление способ определения плотности жидкостей, взвешивая их в небольшом сосуде с узким горлышком. Расширение наверху трубки закрывается притертою стеклянною пробкою. Производят три взвешивания: 1) сосуд, наполненный водою, уравновешивают тарою; 2) тот же сосуд, наполненный жидкостью, плотность которой, меньшую, чем плотность воды, хотят определить, и прибавочную гирю приводят в равновесие с прежнею тарою; 3) пустой сосуд с прибавочною гирею уравновешивают тою же тарою. Если определяемая плотность более, чем воды, то первое взвешивание делают для этой жидкости, а потом уже сосуд с водою. Если вес гири во 2-м взвешивании назвать буквою Q, а в 3-м буквою Q', средний коэффициент расширения жидкостей буквою α, температуру взвешиваемой жидкости буквою t, то из этих данных плотность жидкости, приведенная к 0°, вычисляется по следующей формуле:
[ Δ t — (Q/Q')( Δ t — q)][1 + αt)
где Δ t и q имеют прежнее значение. Особенное развитие этого способа см. "Соединение спирта с водою" Д. И. Менделеева. Для практических целей употребляются спиртомеры или волчки, солемеры, вообще называемые ареометрами (см. эти слова).
4) Разновес, или гири для взвешивания. Точность взвешивания вполне зависит от правильности употребленного разновеса. В настоящее время лучшие механики, изготовляющие разновесы, например Рупрехт в Вене, имеют у себя наборы гирь, тщательно сверенные с нормальными, представляющими означенные на них веса в пустоте. С этих гирь они делают копии высшего порядка точности, производя взвешиваниe в воздухе и определяя плотность новых гирь, чтобы ввести поправку на разность вытесненного воздуха. Обыкновенные же латунные аналитические разновесы копируются в предположении, что их плотность равна плотности нормальных. Свежеприготовленные наборы аналитических разновесов бывают обыкновенно вполне достаточно выверены хорошими механиками, но во время употребления выверка легко портится; гирьки грязнятся, щипчики их царапают, а в химических лабораториях латунь часто окисляется. Ржавчину эту лучше не стирать, как заметил Мор: она поглотила только газ, а, стирая ее, мы удалим и металл, чем еще больше увеличим ошибку, только в обратную сторону. Поэтому не надо забывать проверять старые наборы разновесок и пользоваться полученными проверкою таблицами их поправок. В каталогах физических приборов некоторых механиков помещены недорогие "нормальные" наборы разновесов: они предназначаются для поверки аптекарских торговых гирь и снабжены официальными клеймами, но выверены с меньшею точностью, чем аналитические тех же фирм. Так, французский законодатель допускает погрешность 1,5 грамма для гири в 20 килограммов (0,000075 часть), в 0,15 г для 1 кг (0,00015) и в 0,002 г для одного грамма. Размеры и форму гирь он тоже определяет законом, так что некоторые гири надо делать пустотелыми; при выверке добавляют в пустоту сколько следует материала, ввинчивают головку и закрепляют ее медным шпеньком, на котором мастер должен поставить свое клеймо. У нас ("Устав Торговый", раздел 4, 1845) довольствуются меньшею точностью: для гирь от полуфунта и выше допускается ошибка, не превышающая одну восьмую золотника на каждый фунт, т. е. 0,0013 всей величины, но для малых гирь пропорциональная ошибка больше и доходит до одной доли на золотник, т. е. 0,014. Гири, весы и другие торговые меры дозволяется изготовлять всякому мастеру, получившему на это дозволение от губернского начальства и свидетельство на гербовой бумаге в 90 коп. сер. Выверка и клеймение вновь приготовленных мер производится в казенной палате, а в больших городах — в городской думе (см. еще Весы).
В. Лермантов.
| "БРОКГАУЗ И ЕФРОН" >> "В" >> "ВЕ" >> "ВЕС" >> "ВЕСИ" |
Статья про "Вес и взвешивание." в словаре Брокгауза и Ефрона была прочитана 3711 раз
| Коптим скумбрию в коробке |
| Луковый соус |
TOP 15
- Волос
- Проно
- Степные животные
- Гимнастика
- Индийский океан
- Архитектура
- Сравнение, в литературе
- Манда
- Клитры
- Колесование
- Испарение
- Травоядные животные
- Оплодотворение у pacтений
- Вредные насекомые
- Электризация тел