


БНБ
"БРОКГАУЗ И ЕФРОН" (121188)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Вариационное исчисление
Определение "Вариационное исчисление" в словаре Брокгауза и Ефрона
Вариационное исчисление — История происхождения В. исчисления следующая: в конце XVII и начале XVIII столетия многие знаменитые геометры, как, например, Ньютон, Иоанн и Яков Бернулли, Лейбниц, Маклорен и др., обратили внимание на особый род математических вопросов, в которых требовалось определить вид кривой линии или поверхности при условии, чтобы некоторая величина, зависящая от вида кривой или поверхности, была наибольшая или наименьшая. Впервые встречается подобный вопрос в книге Ньютона: "Philosophiae naturalis principia mathematica", а именно вопрос о форме поверхности тела вращения, испытывающего наименьшее сопротивление движению со стороны окружающей его среды. Другой вопрос того же рода — вопрос о виде брахистохроны, предложенный Иоанном Бернулли (брахистохроной для какой-либо силы называют кривую, по которой материальная точка, подверженная этой силе, переходит в наивозможно краткое время из одной данной точки в другую). По мере накопления подобных вопросов выяснилась необходимость изыскать общий метод для их решения. Такой метод создан Эйлером ("Меthod u s inveniendi lineas curvas maximi vel minimi proprietate gaudentes..." 1744) после 16-летних изысканий над решениями разнообразных вопросов этого рода, и усовершенствован Лагранжем (см. "Th é orie des Fonctions analytiques" и "Le çons sur le Calcul des Foncti ons"). Метод этот есть метод вариаций и назван Лагранжем вариационным исчислением (Calcul des variations).
Простейшие вопросы В. исчисления заключаются в следующем: требуется найти такую функцию от x, которая, будучи подставлена вместо у в данную функцию F от х, у, dy/dx, d2y/dx2..., дала бы интегралу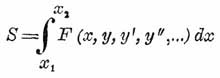
наибольшую или наименьшую величину, при предположении, что х 1 и x2, а также и соответствующие им у 1 и у 2 имеют данные постоянные значения. Например, требуется найти кратчайшую кривую на плоскости между двумя данными точками. В этом случае интеграл, который должен получить наименьшее значение, будет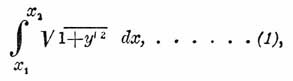
где x1 и x2 суть абциссы данных точек.
Другой пример: требуется провести такую кривую y = f(x) между двумя точками (х 1, у 1) и (x2, y2) на плоскости, чтобы поверхность, образуемая этою кривою при вращении плоскости вокруг оси X -ов, была наименьшею. В этом случае интеграл, долженствующий получить наименьшее значение, будет: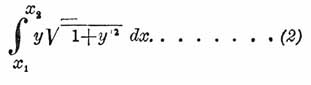
Метод решения подобных вопросов мы вкратце здесь изложим, главным образом для того, чтобы объяснить смысл слов: вариация и вариирование. Предположим, что искомая функция f(x) найдена и что проведена кривая линия y = f(x), делающая интеграл S наибольшим или наименьшим. В функции f(x), кроме x заключается один или несколько параметров, в качестве коэффициентов, оснований степеней, показателей и проч. Изменяя непрерывным образом величины этих параметров, мы получим другие кривые, отличающиеся видом и положением от искомой нами. При изменении параметров на бесконечно малые величины получим кривые, бесконечно близкие к рассматриваемой. Под вариацией от у подразумевается разность между ординатою бесконечно близкой кривой и ординатою рассматриваемой кривой при той же абциссе. Следовательно, вариация ординаты у есть приращение (положительное или отрицательное), получаемое этою ординатою при переходе от рассматриваемой кривой к кривой бесконечно близкой; это приращение обозначается через δ у. Выше было сказано, что бесконечно близкая кривая получается через бесконсчно малое изменение параметров. Пусть параметры f(x) суть α, β, γ; бесконечно малые приращения их означим через δα, δβ, δγ . Пренебрегая бесконечно малыми величинами второго и высших порядков, можем выразить δ у так:
δ y = [df(x)/d α ] δα + [df(x)/d β ] δβ + [df(x)/d γ ] δγ .
Следовательно, варьирование ординаты у, или f(х) может быть рассматриваемо как дифференцирование по параметрам кривой.
При варьировании f(х) производные у', y" от функции по x также получают бесконечно малые приращения, которые мы обозначим так: δ у', δ y", Эти вариации производных можно представить так, например, δ у':
δ y' = (ddy/d α dx) δα + (ddy/d β dx) δβ + (ddy/d γ dx) δγ
а так как изменения параметров совершенно не зависят от изменений абцисс x, то можно переменить порядок действий получения производных по x и по параметрам; самые приращения δα, δβ, δγ от x не зависят, а потому:
δ y' = d/dx[(dy/d α) δα + (dy/d β) δβ + (dy/d γ) δγ ] = d δ y/dx (A).
Точно так же можно показать, что:
δ y" = d2 δ y/dx2 ,(A1) и т. д.
При варьировании у, функция F(x, y, у', у",... ) получает приращение, равное:
Δ F = F(x, y + δ y, y' + δ y',) — F(x, y, y',).
Это приращение может быть представлено в виде ряда, расположенного по возрастающим степеням вариаций δ y, δ y', δ y". Вариацией первого порядка функции F называется та часть этого приращения, которая заключает сумму членов с первыми степенями вариаций δ у, δ y', δ y" Эта вариация первого порядка от F обозначается также знаком δ, так что
δ F = (dF/dy) δ y + (dF/dy') δ y' + (dF/dy") δ y" +
Удвоенную сумму тех членов приращения F, которые заключают вторые степени и произведения вариаций δ у, δ у, δ у" по две, называют вариацией второго порядка от функции F и обозначают ее так: δ 2F.
Если составить выражение приращения, получаемого интегралом (S), при варьировании ординаты у , то найдем, что оно равняется интегралу от Δ F и поэтому может быть представлено в виде суммы членов различного порядка малости. Сумма членов первого порядка малости образует вариацию первого порядка интеграла S: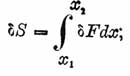
Удвоенная сумма членов второго порядка малости образует вариацию второго порядка: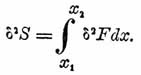
Составленное выражение δ S может быть преобразовано таким образом, что оно будет заключать только δ у, но не будет заключать вариаций от производных. На основании равенства (А), (А 1) и прочих дальнейших равенств того же рода, каждая из этих вариаций равняется соответственной производной по x от δ у. Вследствие этого, помощью интегрирований по частям и приняв во внимание, что δ у 1 = 0 и δ у 2 = 0 (так как y1 и у 2 имеют данные постоянные значения), получим: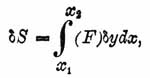
где
(F) = dF/dy — d/dx(dF/dy') + d2/dx2(dF/dy")
Для того, чтобы интеграл S был наибольшим или наименьшим, необходимо, чтобы δ S была равна нулю, какою бы функцией от x ни была δ у; а это вследствие разнообразия и произвольности вариаций δ у возможно только тогда, когда (F) = 0. Этому-то дифференциальному уравнению и должна удовлетворять функция у = f(x), делающая S наибольшим или наименьшим.
Так, например, функция, делающая интеграл (1) наибольшим или наименьшим, должна удовлетворять дифференциальному уравнению: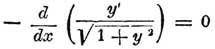
из которого следует, что у' = С и у = Сх + С 1, где С и C1 — постоянные. Как и следовало ожидать, искомая линия — прямая.
Кривая, делающая интеграл (2) наибольшим или наименьшим, окажется цепною линией.
С надлежащими изменениями и дополнениями метод этот применяется и к тем случаям, когда не задаются точки, между которыми должна быть проведена кривая, а также и к тем случаям, когда ищется кривая, делающая интеграл S наибольшим или наименьшим, и вместе с тем делающая другой интеграл равным данной величине; последние вопросы принадлежат к роду вопросов об относительных maxima и minima. Затем этот метод распространяется и на вопросы более высшего рода, в которых требуется определение вида поверхностей, делающих наибольшим или наименьшим двойной интеграл данного вида и далее. В числе геометров, усовершенствовавших метод варьирования в применении к нахождению maxima и minima кратных интегралов, были: Гаусс ("Principia generalia theoriae figurae fluidorum in statu aequilibrii", "Gesammelte Werke" Bd. V); Пуассон (в "M émoires de l'Acadé mie des Sciences", vol. 12, 1833) — в применении к двойным интегралам; Остроградский ("M é moire sur le calcul des variations des integrales multiples", в "Mem. de l'Acad. des Sciences de S-P é tersb." 1838; "Crelle's Journal", vol. XV), давший изящное выражение вариации многократного интеграла; Якоби ("Zur Theorie der Variations-rechnung und der Differentialgleichungen", в "Gesam. Werke", т. IV), положивший основание метода определения знака вариации второго порядка однократного интеграла. Достаточно полным руководством вариационного исчисления может служить: "Calcul des Variations р. Moigno et Lindel ö f" (1861, четвертый том "Le ç ons de Calcul differentiel et integral p. Moigno"). История вариац. исчисления, начиная с Лагранжа и до 1860 г., изложена в книге Todhunter: "A History of the Progress of the Calculus of Variations during the nineteenth Century", 1861. О применении В. исчисления к механике см. статьи: Дифференциальные уравнения движения, Действие (начало наименьшего действия), Начало Гамильтона.
Д. Бобылев.
| "БРОКГАУЗ И ЕФРОН" >> "В" >> "ВА" >> "ВАР" >> "ВАРИ" |
Статья про "Вариационное исчисление" в словаре Брокгауза и Ефрона была прочитана 982 раз
| Бургер двойного помола |
| Гороховое пюре |
TOP 15
- Волос
- Проно
- Степные животные
- Гимнастика
- Индийский океан
- Архитектура
- Сравнение, в литературе
- Манда
- Клитры
- Колесование
- Испарение
- Травоядные животные
- Оплодотворение у pacтений
- Вредные насекомые
- Электризация тел